
Тема 2. Аналитическая геометрия
Программный объем темы:
1. Декартова и полярная системы координат. Переход из одной системы в другую.
2. Параллельный перенос координатных осей.
3. Основные виды уравнения прямой на плоскости и в пространстве. Основные виды уравнения плоскости.
4. Кривые второго порядка, их канонические уравнения и графики. Приведение уравнений кривых второго порядка к каноническому виду.
ДЕКАРТОВА И ПОЛЯРНАЯ СИСТЕМЫ КООРДИНАТ
Если
на плоскости задана прямоугольная
декартова система координат
![]() ,
то точку
,
то точку![]() этой плоскости, имеющую координаты
этой плоскости, имеющую координаты![]() и
и![]() ,
обозначают
,
обозначают![]() .
.
Расстояние
![]() между точками
между точками![]() и
и![]() определяется по формуле
определяется по формуле![]() .
.
В
полярной системе координат положение
точки
![]() на плоскости определяется ее расстоянием
на плоскости определяется ее расстоянием![]() от полюса
от полюса![]() (
(![]() -
полярный радиус-вектор точки). Угол
-
полярный радиус-вектор точки). Угол![]() считается положительным при отсчете
от полярной оси против часовой стрелки.
считается положительным при отсчете
от полярной оси против часовой стрелки.
Если
начало декартовой прямоугольной системы
координат совместить с полюсом, а
ось
![]() направить по полярной оси, то прямоугольные
координаты
направить по полярной оси, то прямоугольные
координаты![]() и
и![]() точки
точки![]() и ее полярные координаты
и ее полярные координаты![]() и
и![]() связаны следующими формулами:
связаны следующими формулами:
![]()
Так
как
![]() –
расстояние, то
–
расстояние, то![]() .
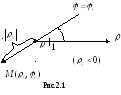
Обычно это ограничение снимают. Тогда
получается обобщенная полярная система
координат. Положение точки
.
Обычно это ограничение снимают. Тогда
получается обобщенная полярная система
координат. Положение точки
![]() в такой системе определяется следующим
образом. Проводим из полюса луч
в такой системе определяется следующим
образом. Проводим из полюса луч
![]() ,
продляем его за полюс и на его продолжении
откладываем отрезок, равный по длине
,
продляем его за полюс и на его продолжении
откладываем отрезок, равный по длине
![]() (рис
2.1).
(рис
2.1).
В задании 2.5 кривые требуется построить в обобщенной полярной системе координат.
Пример.
В
обобщенной полярной системе координат
построить кривую
![]() .
.
Д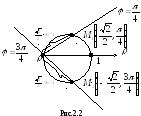 ля
решения задачи следует найти точки,
лежащие на кривой, давая
ля
решения задачи следует найти точки,
лежащие на кривой, давая![]()
![]() значения
через какой-то промежуток (чем меньше
промежуток, тем точнее можно построить
кривую, но тем больше объем вычислительной
работы). Результат построения – окружность
с диаметром
значения
через какой-то промежуток (чем меньше
промежуток, тем точнее можно построить
кривую, но тем больше объем вычислительной
работы). Результат построения – окружность
с диаметром![]() – приведен на рис. 2.2. Там же показаны
две точки,
– приведен на рис. 2.2. Там же показаны
две точки,![]() и
и![]() ,
принадлежащие этой окружности, способ
построения которых ясен из рисунка.
Любые другие точки этой кривой строятся
аналогично.
,
принадлежащие этой окружности, способ
построения которых ясен из рисунка.
Любые другие точки этой кривой строятся
аналогично.
Всякой
линии на плоскости
![]() ,
рассматриваемой как множество точек,
соответствует некоторое уравнение, в
которое входят координаты любой точки
,
рассматриваемой как множество точек,
соответствует некоторое уравнение, в
которое входят координаты любой точки![]() ("текущей точки"), лежащей на этой
линии. Такое уравнение называется
уравнением данной линии.
("текущей точки"), лежащей на этой
линии. Такое уравнение называется
уравнением данной линии.
Чтобы составить уравнение линии как геометрического места точек, обладающих одинаковым свойством, нужно:
1)
взять произвольную (текущую) точку
![]() линии,
линии,
2)
записать равенством общее свойство
всех точек
![]() линии,
линии,
3)
входящие в это равенство отрезки (и
углы) выразить через текущие координаты
точки
![]() и через данные в задаче.
и через данные в задаче.
Пример.
В декартовой прямоугольной системе
координат вывести уравнение геометрического
места точек, сумма квадратов расстояний
которых до двух данных точек
![]() и
и![]() есть величина постоянная, равная 47.
есть величина постоянная, равная 47.
Решение.
Обозначим
буквой
![]() произвольную точку линии.
произвольную точку линии.
![]() и
и
![]() - текущие координаты этой точки.
- текущие координаты этой точки.
Запишем геометрическое свойство линии символически.
![]() . (1)
. (1)
Выразим
![]() и
и![]() через текущие координаты точки
через текущие координаты точки![]() :
:
![]()
Подставив
полученные выражения в равенство (1),
найдем уравнение, связывающее
координаты
![]() точки
точки![]() :
:
![]()
Упростим последнее уравнение:
![]()
![]()
![]()
![]()
Получили
уравнение окружности с центром в т.
(0,1) и радиусом![]() .
.
ПРЯМАЯ НА ПЛОСКОСТИ
Прямая
на плоскости в декартовой прямоугольной
системе координат
![]() может быть задана уравнением одного из
следующих видов:
может быть задана уравнением одного из
следующих видов:
1)
![]() - общее уравнение прямой.
- общее уравнение прямой.
![]() -
координаты нормального вектора
-
координаты нормального вектора
![]() прямой (вектора, перпендикулярного
данной прямой).
прямой (вектора, перпендикулярного
данной прямой).
2)
![]() -
уравнение прямой, проходящей через
точку
-
уравнение прямой, проходящей через
точку![]() перпендикулярно вектору
перпендикулярно вектору![]() .
.
3)
![]() -
уравнение с угловым коэффициентом, где
-
уравнение с угловым коэффициентом, где![]() - отрезок, отсекаемый прямой на оси
- отрезок, отсекаемый прямой на оси![]() ,
,![]() или
или![]() ,
где
,
где![]() - угол наклона прямой к оси
- угол наклона прямой к оси![]() .
.
4)
![]() - уравнение прямой с угловым коэффициентом
- уравнение прямой с угловым коэффициентом
![]() ,
проходящей через данную т.
,
проходящей через данную т.
![]() .
.
5)
![]() - каноническое уравнение прямой, или
уравнение прямой, проходящей через т.
- каноническое уравнение прямой, или
уравнение прямой, проходящей через т.![]() параллельно направляющему вектору
параллельно направляющему вектору
![]() .
.
6)
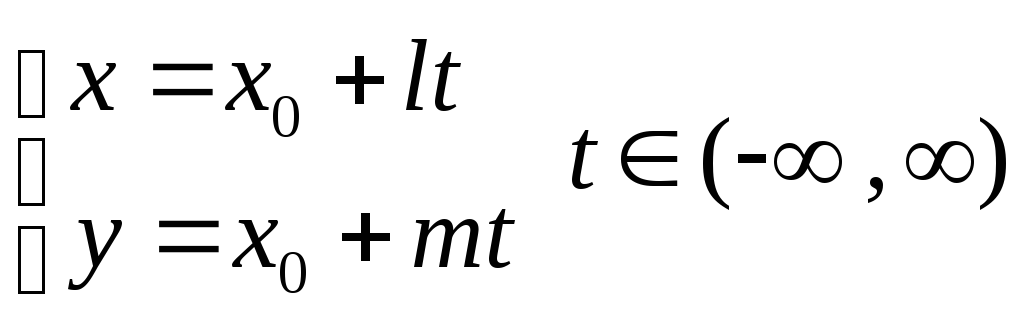 - параметрические уравнения прямой,
- параметрические уравнения прямой,
![]() -
параметр.
-
параметр.
7)
![]() - уравнение прямой в отрезках, где
- уравнение прямой в отрезках, где
![]() и
и
![]() - величины отрезков, отсекаемых прямой
на координатных осях
- величины отрезков, отсекаемых прямой
на координатных осях![]() и
и![]() соответственно.
соответственно.
8)
![]() - уравнение прямой, проходящей через
две данные точки
- уравнение прямой, проходящей через
две данные точки
![]() и
и
![]() .
.
Угол
между двумя прямыми можно найти, зная
угловые коэффициенты прямых:
![]() .
.
Условие
параллельности двух прямых:
![]() или
или
![]() .
.
Условие
перпендикулярности двух прямых:
![]() ,
или
,
или![]() .
.
плоскость
Плоскость
![]() в декартовой прямоугольной системе
координат
в декартовой прямоугольной системе
координат
![]() может быть задана уравнением одного из
следующих видов:
может быть задана уравнением одного из
следующих видов:
1)
![]() - общее уравнение плоскости,
- общее уравнение плоскости,![]() - нормальный вектор плоскости,
- нормальный вектор плоскости,![]() - его координаты;
- его координаты;
2)
![]() - уравнение плоскости, проходящей через
т.
- уравнение плоскости, проходящей через
т.![]() перпендикулярно
нормальному вектору
перпендикулярно
нормальному вектору![]() .
.
3)
![]() - уравнение плоскости в отрезках, где
- уравнение плоскости в отрезках, где![]() - отрезки, отсекаемые плоскостью на осях
координат
- отрезки, отсекаемые плоскостью на осях
координат![]() соответственно.
соответственно.
4)
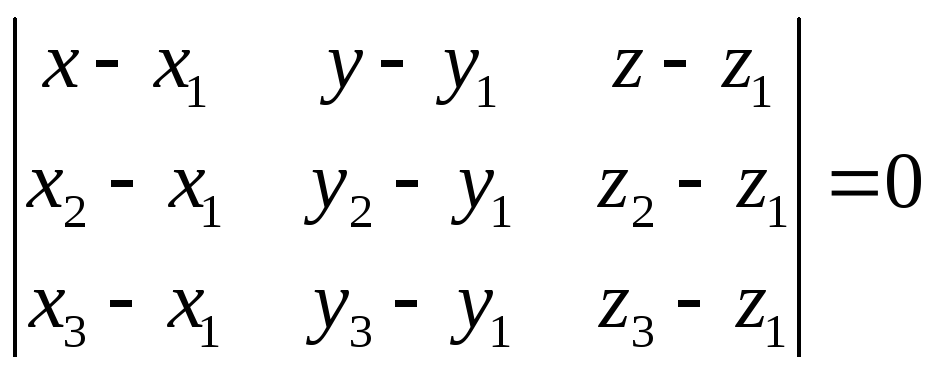 - уравнение плоскости, проходящей через
три данные точки:
- уравнение плоскости, проходящей через
три данные точки:
![]()
![]()
![]() .
.
ПРЯМАЯ В ПРОСТРАНСТВЕ
Прямая в пространстве может быть задана:
1) общими уравнениями:
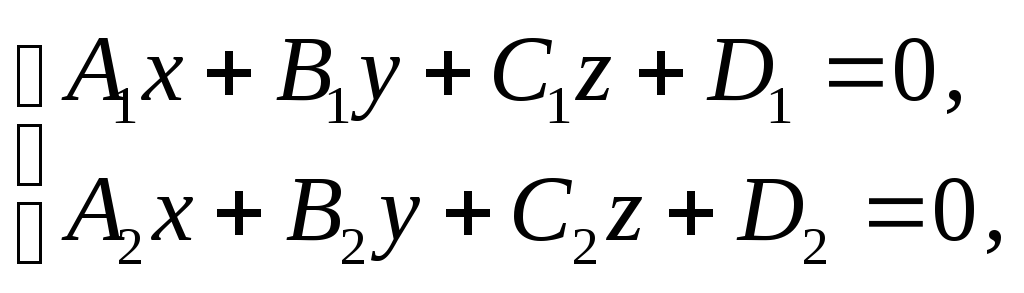
т.е. системой уравнений двух пересекающихся плоскостей.
2) параметрическими уравнениями:

где
![]() - координаты данной точки, а
- координаты данной точки, а![]() – координаты направляющего вектора
прямой
– координаты направляющего вектора
прямой![]() ,
т.е. вектора, параллельного данной
прямой;
,
т.е. вектора, параллельного данной
прямой;
3) каноническими уравнениями:
![]()
4) уравнениями прямой, проходящей через две точки:
![]() и
и
![]() :
:
![]()
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
И ПРЯМЫХ В ПРОСТРАНСТВЕ
Угол
![]() между плоскостями
между плоскостями![]() и
и![]() определяется по формуле
определяется по формуле
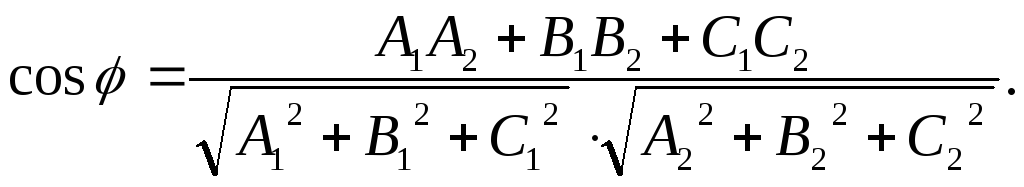
Условие перпендикулярности плоскостей:
![]()
Условие
параллельности плоскостей:
![]()
Расстояние
от точки
![]() до плоскости, определяемой уравнением
до плоскости, определяемой уравнением![]() можно найти по формуле
можно найти по формуле
![]()
Угол между двумя прямыми в пространстве, заданными их каноническими уравнениями, определяется по формуле
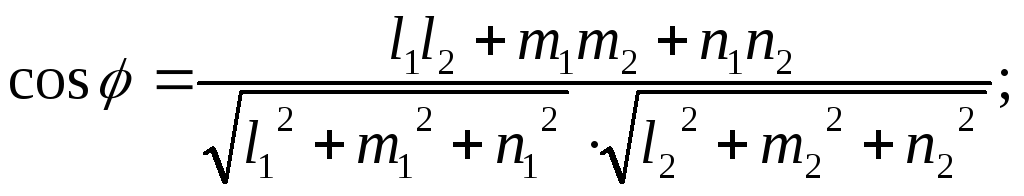
условие
параллельности двух прямых:
![]() условие перпендикулярности двух прямых:
условие перпендикулярности двух прямых:![]() Угол между прямой и плоскостью определяется
по формуле
Угол между прямой и плоскостью определяется
по формуле
![]()
условие
параллельности прямой и плоскости:
![]()
условие
перпендикулярности прямой и плоскости:
![]() .
.
При решении задач надо уметь переходить от общих уравнений прямой в пространстве к каноническим.
Пример.
По
уравнениям плоскостей
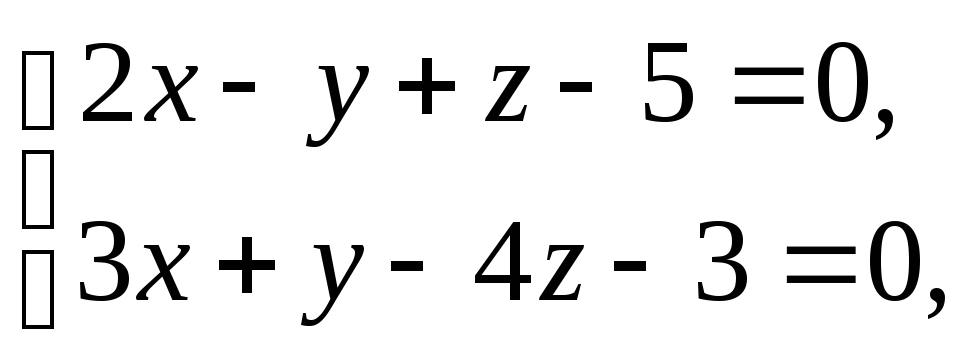
образующих
прямую, составить ее уравнения в
каноническом виде. Решение. Определим
координаты одной точки прямой: положим
![]() ,
тогда для значений
,
тогда для значений![]() и
и![]() решим систему уравнений
решим систему уравнений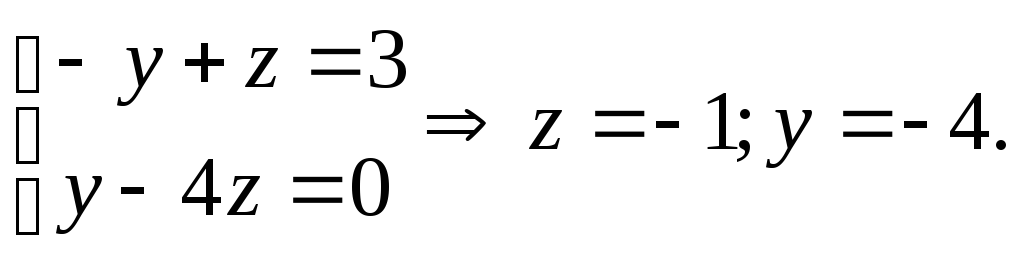
Теперь канонические уравнения имеют вид
![]()
Направляющий
вектор
![]() искомой прямой будет перпендикулярен
нормальным векторам
искомой прямой будет перпендикулярен
нормальным векторам![]() и
и![]() данных плоскостей, следовательно, его
координаты можно найти, используя
векторное произведение.
данных плоскостей, следовательно, его
координаты можно найти, используя
векторное произведение.
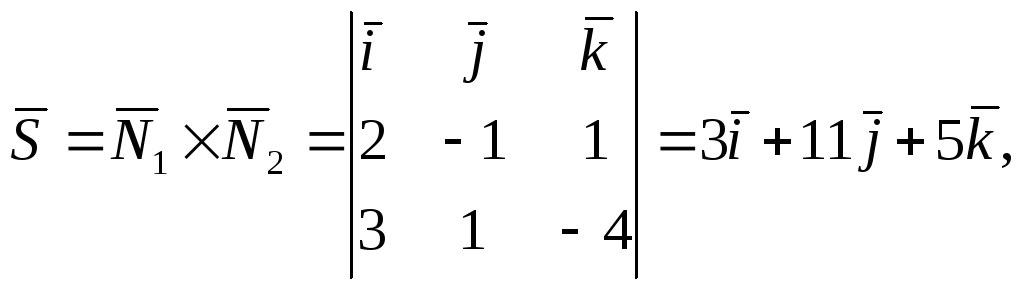 т.е.
т.е.
![]()
Канонические уравнения искомой прямой имеют вид
![]()
КРИВЫЕ ВТОРОГО ПОРЯДКА
