20. Достаточные условия существования экстремума.

Разложим R(x) в окрестности точки, подозреваемой на экстремум

x₀=col()

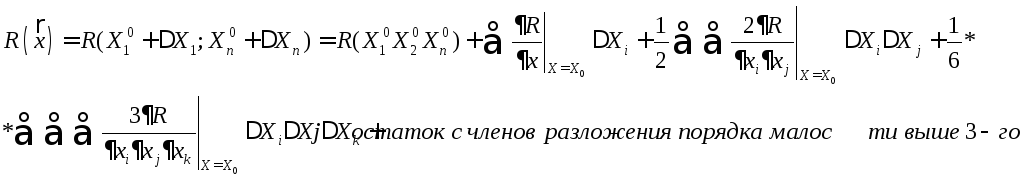
X⁰ удовлетворяет необходимым условиям существования R, тогда

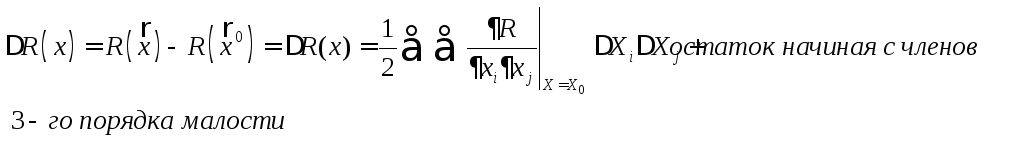(3)

Из выражения (3) следует, то что, если пренебречь членами порядка малости выше 2-го знака приращения «±» определяется всеми производными 2-ого порядка, включая и смешанные. Частные производные вычисляются в т.и их можно рассматривать как константы, поэтому необязательно требовать малости:

,

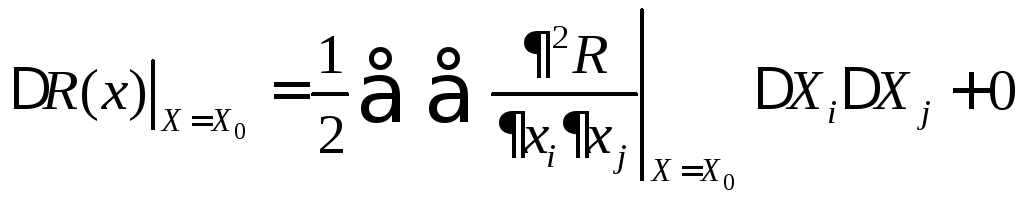обозначим

Если при любых и, кроме,Z²>0, а в точке 1 Z²=0, то Z² положительно определена и в точке экстремума будет иметь минимум >0. Для положительной определенности квадратичной формыZ² необходимо и достаточно чтобы все определители состояли из элементов и были положительны.

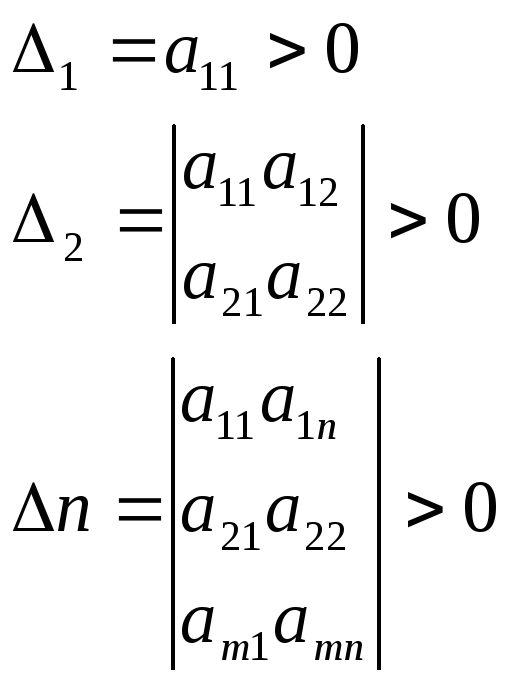, тогда Х⁰ – доставляет min .

Условия Сильвестра.

Таким образом, если все определители Сильвестра положительны, то в точке экстремума имеем минимум : Х⁰ = arg minЕсли определитель Сильвестра нечетного порядка «-» , а четного «+», то в точке экстремума имеем максимум. При другой последовательности чередования знаков определителей Сильвестра в точкеэкстремума нет. Например, точкаявляется «…». (Рис. 20.1).

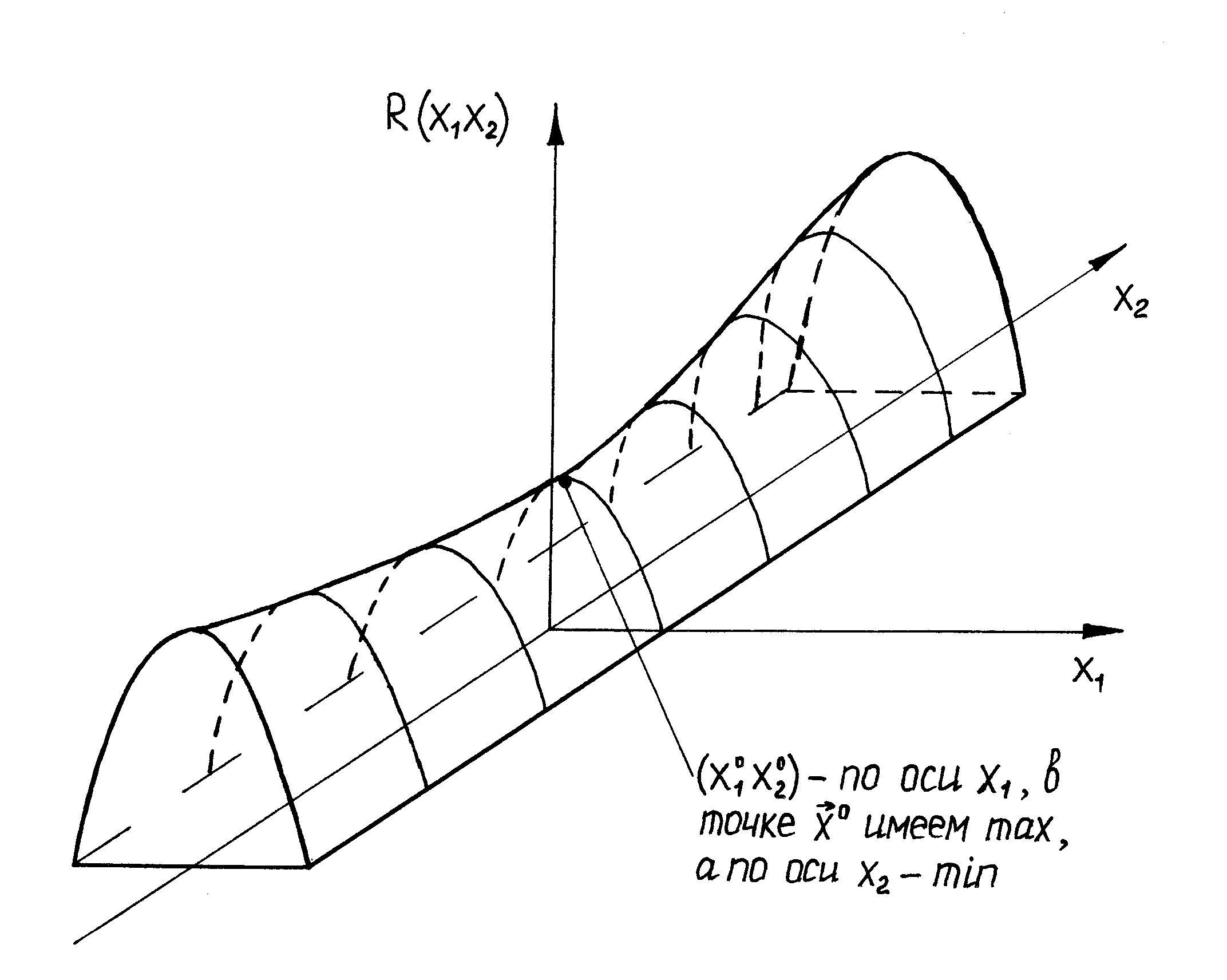
Рис. 20.1

22. Задачи на условный экстремум. Теорема Куна-Теккера.

Пояснения к рис. 22.1.

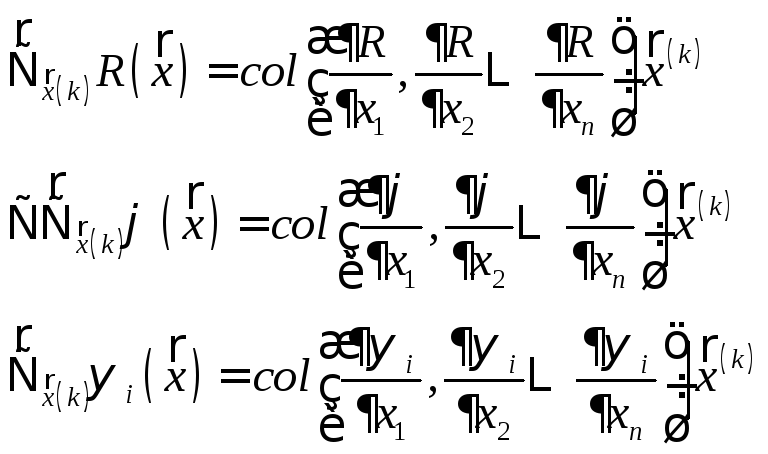
Границы допустимой области составлены из отрезков линий:

Если решение лежит внутри допустимой области → ограничение в форме неравенств неактивны, тогда решение задачи можно свести к более простому случаю с ограничениями в форме неравенств поэтому особый интерес представляют решения находящиеся на границе данной области и особенно в угловых точках, где активны два ограничения в форме неравенств. Пусть это будут <0 и<0 – это условие когдаmax R в угловой точке, т. к. через нее проходит линия = 0. Построим в точке С градиенты всех функций. Градиент перпендикулярен касательной к точке и указывает направление наибольшего возрастания функций. Пусть в точкеС функция R(х) достигает условного максимума, т.к. показывает направление наибольшего возрастанияR, то он должен образовывать тупой угол с направлением L к касательной = 0 в точкеС. иL должны лежать по разные стороны от линии, по которой направлен и по одну сторону си. Проведем биссектрису угла образованнуюи, т.к.,илежат по одну сторону от линииR. В этом направлении точка С до пересечения L и α обозначим через вектор V.

(*1)

(*2)

больше 0, больше 0

(*4)

Аналогичный результат б. получен, если активно т. 1 ограничение , т.е.точка С пренадлежит линии.

Теорема. Условия (*3), (*4) справедливы и для задачи (1)-(3) т.е. м. сформулировать теорему Куна-Таккера. Если функция целевая при наличии ограничений типа равенств и неравенств достигает условного экстремума в некоторой точке С, к. пренадлежит допустимой области, то существуют такие положительные числа,,…и, из которых хотя бы 1 отлично от 0, такие числа,

что и длявыполняется следующия соотношения:

(*5)

(*6)

Поэтому принято больше 0.

Вывод теоремы был сделан для случая max , т о,все остальное остается в силе

матрицы от руки пиши

Система (**5) дополняется условиями (*6). Нужно решить систему (*%) и найти экстримум. (*5),(*6) – необходимые условия существования экстримума при ограничении типа равенств и неравенств.