
- •1. Классификация гидравлических машин.
- •2. Насосы. Общие сведения.
- •3. Закон перемещения поршня.
- •4.Подача насоса. График подачи.
- •5. Степень неравномерности подачи
- •6. Анализ изменения давления в цилиндре насоса в период всасывания
- •6. Анализ изменения давления в цилиндре насоса в период нагнетания
- •7. Расчет процесса всасывания поршневого (плунжерного) насоса.
- •7. Конструкции насосов.
- •7.1. Насос нбт-600
- •7.2. Насос у8-6м
- •8. Узлы и детали насосов.
- •8.1. Гидравлические коробки.
- •8.2. Станина бурового насоса.
- •8.4. Клапаны.
- •8.4.1. Основы теории тарельчатого клапана
- •8.4.2. Расчет клапана.
- •8.5. Пневмокомпенсаторы
- •8.6. Предохранительные устройства
- •8.7. Пусковые задвижки
6. Анализ изменения давления в цилиндре насоса в период нагнетания
Рассмотрим процесс нагнетания жидкости одноцилиндровым насосом одинарного действия в нагнетательную линию общей длиной lн, состоящий из нескольких участков различного диаметра (рис. 10). Ось цилиндра насоса расположена горизонтально, геометрическая высота нагнетания равна zн, перекачиваемая жидкость имеет плотность ρ, в конце нагнетательного трубопровода поддерживается постоянное давление pк.
Запишем уравнение Бернулли для сечений 2–2 и 3–3:
![]() ,
(39)
,
(39)
где р2=рц–давление жидкости
в цилиндре насоса;v2=vп–скорость движения
жидкости в цилиндре, равная скорости
перемещения поршня;р3=рк– давление жидкости
в конце нагнетательного трубопровода;
v3=vк– скорость движения
жидкости в конечном сечении нагнетательного
трубопровода;
![]() –потери напора
между рассматриваемыми сечениями 2-2 и
3-3.
–потери напора
между рассматриваемыми сечениями 2-2 и
3-3.
Перепишем уравнение (39) с учетом приведенных замечаний:
![]() .
(40)
.
(40)
Потери энергии
![]() между сечениями 2-2 и 3-3 состоят из потерь
в местных сопротивлениях
между сечениями 2-2 и 3-3 состоят из потерь
в местных сопротивлениях![]() нагнетательного
трубопровода, потерь по длине
нагнетательного
трубопровода, потерь по длине
![]() и потерь на преодоление сил инерции в
цилиндре
и потерь на преодоление сил инерции в
цилиндре![]() и
в трубопроводе
и
в трубопроводе![]() .
.
При этом учтем, что потери в нагнетательном клапане изменяются аналогично потерям во всасывающем клапане, поэтому выделим эти потери в виде отдельного слагаемого. Местные потери представим в виде:
![]() =
=![]() ,
(41)
,
(41)
где
![]() – потери напора в нагнетательном
клапане;
– потери напора в нагнетательном
клапане;![]() – скорость движения жидкости вi-м
участке нагнетательного трубопровода;
– скорость движения жидкости вi-м
участке нагнетательного трубопровода;
![]() – коэффициент местных потерьi-го
местного сопротивления нагнетательного
трубопровода.
– коэффициент местных потерьi-го
местного сопротивления нагнетательного
трубопровода.
Выразив в уравнении (41) скорость движения жидкости в трубопроводе через скорость поршня, получим:
![]() =
=![]() +
+![]() ,
(42)
,
(42)
где
![]() –
площадь поперечного сеченияi-го
участка нагнетательного трубопровода.
–
площадь поперечного сеченияi-го
участка нагнетательного трубопровода.
Потери напора по
длине
![]() нагнетательного трубопровода, состоящего
изj
участков длиной ljн
с диаметрами djн
площадью поперечного сечения fjн
как и ранее, вычислим по известной
формуле Дарси-Вейсбаха:
нагнетательного трубопровода, состоящего
изj
участков длиной ljн
с диаметрами djн
площадью поперечного сечения fjн
как и ранее, вычислим по известной
формуле Дарси-Вейсбаха:
![]() =
=![]() ,
(43)
,
(43)
где λjн – коэффициент гидравлического трения на j-м участке.
С учетом отмеченных замечаний и обозначений, уравнение (40) примет вид:
 .
(44)
.
(44)
Выражение, стоящее в квадратных скобках представляет собой сумму потерь в местных сопротивлениях и потерь по длине. Выполнив преобразование этого выражения, получим:
 =
=
![]() ,
(45)
,
(45)
где
![]() – приведенный коэффициент гидравлических
сопротивлений нагнетательного
трубопровода.
– приведенный коэффициент гидравлических
сопротивлений нагнетательного
трубопровода.
Подставим в уравнение (44) уравнение (45) и выразим скорость движения жидкости vк в конечном сечении нагнетательного трубопровода через скорость поршня:

 (46)
(46)
Подставив в уравнение (46) скорость поршня по уравнению (34), получим:
![]()
 (47)
(47)
Потери напора на преодоление сил инерции жидкости в цилиндре и нагнетательном трубопроводе вычислим аналогично всасывающему трубопроводу:
![]()
 .
(48)
.
(48)
Потери напора на преодоление сил инерции в j-м участке нагнетательного трубопровода вычислим по формуле:
![]()
 ,
(49)
,
(49)
где ![]() - длина j-го
участка нагнетательного трубопровода.
- длина j-го
участка нагнетательного трубопровода.
Сумма потерь на преодоление сил инерции по всей длине нагнетательного трубопровода будет равна сумме потерь во всех его участках:
![]() ,
(50)
,
(50)
где Lн – приведённая длина нагнетательного трубопровода.
Заменив в уравнениях (48) и (50) cosφ по выражению (29) соответственно получим:
![]()
![]() (48а);
(48а); ![]() (50а)
(50а)
Подставив в уравнение (47) потери напора на преодоление сил инерции жидкости в цилиндре и нагнетательном трубопроводе по уравнениям (48а) и (50а) и умножив правую и левую часть уравнения (47) на (ρ∙g), получим:
Pц=Pк+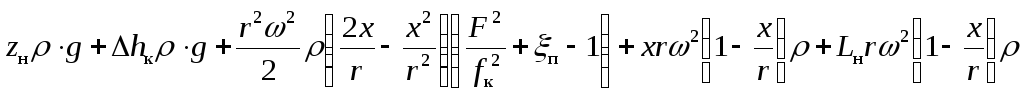 .
(51)
.
(51)
 На
рис. 12 приведена графическая зависимость
давления в цилиндре насоса в период
нагнетания, построенная по уравнению
(51). При построении графика нужно иметь
в виду, что к моменту начала нагнетания
поршень насоса совершил полный ход
равныйS=2r.
Поэтому текущая координата х,
характеризующая положение поршня будет
равна:
На
рис. 12 приведена графическая зависимость
давления в цилиндре насоса в период
нагнетания, построенная по уравнению
(51). При построении графика нужно иметь
в виду, что к моменту начала нагнетания
поршень насоса совершил полный ход
равныйS=2r.
Поэтому текущая координата х,
характеризующая положение поршня будет
равна:
х= S–хн
Максимальное давление в цилиндре насоса будет в начале нагнетания, т.е. при х=0, а минимальное – в конце нагнетания при х=2r.
Pцmax=Pк+![]() ;
;
Pцmin=Pк+![]() .
.
