Примеры
3.15.Вентиляционная трубаd=0,1м
(100 мм) имеет длину
.
Определить давление, которое должен
развивать вентилятор, если расход
воздуха, подаваемый по трубе,
.
Давление на выходе
.
Местных сопротивлений по пути не имеется.
Температура воздуха 20˚ C. Труба стальная
новая, бесшовная.
Решение.Находим скорость воздуха в трубе:
.
Число Рейнольдса для потока воздуха в
трубе при
(табл. П‑8)
.
Относительная шероховатость (по табл.
П-15
)
.
Коэффициент гидравлического трения
.
По формуле Дарси-Вейсбаха находим потери
давления на трение (
):
.
Ответ: 
.
3.16.Расход воды при температуре 10˚
C в горизонтальной трубе кольцевого
сечения, состоящей из двух концентрических
оцинкованных стальных труб (при
),
.
Внутренняя труба имеет наружный диаметрd=0,075 м, а наружная труба
имеет внутренний диаметрD= 0,1м. Найти потери напора на трение на
длине трубыl=300м.
Решение.Площадь живого сечения
.
Смоченный периметр живого сечения
.
Эквивалентный диаметр
Относительная шероховатость
.
Средняя скорость течения
.
Число Рейнольдса при
(см. табл. П-12)
.
Коэффициент гидравлического трения
.
Потери напора на трение по длине находим по формуле Дарси-Вейсбаха:
.
Ответ: 
.
3.17.Определить расходы воды в трубе
прямоугольного поперечного сечения с
отношением сторон a:b = 0,25 и в круглой
трубе при той же площади поперечного
сечения
,
если потери давления в этих трубах
одинаковы и равны
,
а длина каждой трубы
.
Температура воды 20˚ C.
Решение.Для трубы круглого сечения
;
для трубы прямоугольного сечения при
a:b = 0,25
.
Найдём эквивалентные диаметры для этих
труб :
;
.
Потери давления определяем по формуле
Дарси-Вейсбаха. Предположим первоначально,
что режим течения в трубах ламинарный.
Тогда по формуле
,
где значение коэффициента формы А (см.
табл. П-24) для круглых труб равно 64, для
прямоугольных – 73, найдем коэффициент
Дарси.
Формула потерь давления принимает вид
.
Для круглой трубы при плотности воды
(см.
табл. П-4) и вязкости
(см. табл. П-12)
;
для прямоугольной трубы
Определяем числа Рейнольдса:
для круглой трубы
;
для прямоугольной трубы
.
Поскольку числа Рейнольдса меньше критического равного 2 320, режим течения в трубах, как и предполагалось, ламинарный.
Расход воды:
в круглой трубе
;
в прямоугольной трубе
.
Таким образом, в условиях ламинарного движения при одной и той же площади живого сечения и одинаковых потерях давления круглая труба пропускает расход в 2,5 раза больший, чем труба прямоугольного сечения.
Ответ: 
;
.
3.18.Определить диаметр d нового
стального трубопровода длиной
,
который должен пропускать расход воды
,
при потерях давления
.
Температура подаваемой воды 20˚ C.
Решение.Предполагаем, что трубопровод работает в квадратичной области сопротивления, тогда найдем коэффициент Дарси по формуле Шифринсона
,
где
(см. табл. П-15).
Найдем среднюю скорость течения по формуле Дарси-Вейсбаха
.
Подставляя в это выражение формулу для λ и учитывая, что расход
получим
.
Для условий задачи при
(см.
табл. П-4)
;
d=0,15м.
Площадь поперечного сечения трубы составит
.
Скорость в трубопроводе равна
.
Число Рейнольдса при
(см. табл. П-12)
.
При относительной шероховатости
и числе Рейнольдса
,
согласно рис.3.1, находим, что трубопровод
работает в зоне переходного сопротивления.
Значения λ определяем по формуле Альтшуля:
.
Тогда
;
;
d=0,12м.
Проверка показала, что при d=0,12м и скорости 1,75м/с трубопровод работает в зоне переходного сопротивления.
Уточним значение λ:
;
;
.
При λ=0,018
;
;d=0,118м.
Ответ: d=0,118м.
3.19.Определить расход воды в бывшей
в эксплуатации водопроводной трубе
диаметромd=0,3м, если
скорость на оси трубы, замеренная трубкой
Пито – Прандтля
,
а температура воды 10˚ C.
Решение.Находим по табл. П-15 значение
абсолютной шероховатости для старых
стальных труб:
.
Предполагая, что движение воды происходит в квадратичной области турбулентного движения, определяем коэффициент гидравлического трения по формуле Шифринсона:
.
Среднюю скорость определяем по уравнению:
;
.
Кинематическая вязкость воды
(см. табл. П-12).
Определяем значение критерия зоны турбулентности по формуле:
.
Таким образом, движение действительно происходит в квадратичной области сопротивления.
Расход воды в трубе находим из выражения
.
Ответ: 
.
3.20.Для ограничения расхода воды в
водопроводной линии установлена
диафрагма. Избыточные давления в трубе
до и после диафрагмы постоянны и равны
соответственно
и
.
Диаметр трубыD=0,076 м.
Определить необходимый диаметр отверстия
диафрагмыdс таким
расчётом, чтобы расход в линии был равен
.
Решение. Потеря напора в диафрагме
.
Скорость воды в трубопроводе
.
Из формулы Вейсбаха
имеем:
.
Этому значению коэффициента сопротивления
соответствует отношение площадей
сечения
,которое
можно определить из следующей формулы:
,
где коэффициент сжатия струи находим по формуле:
.
Таким образом,
;
;
;
;
.
Находим диаметр отверстия диафрагмы:
.
Коэффициент сжатия струи
.
Ответ: 
.
3.21.Вода протекает по горизонтальной трубе, внезапно сужающейся отd1=0,2 м доd2=0,1 м. Расход водыQ=0,02 м3/с. Определить, какую разность уровней ртутиhртпокажет дифференциальный манометр, включенный в месте изменения сечения. Температура воды 200С.
Решение. Скорость воды в широком сечении трубы
Скорость воды в узком сечении трубы
Степень сужения трубопровода
Коэффициент сжатия струи находим по формуле:
Коэффициент местного сопротивления при внезапном сужении определяем по формуле:
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения, совпадающей с осью трубы,
Разность пьезометрических напоров
Величина столба ртутного манометра
Ответ: 
3.22.В закрытом резервуаре А
поддерживается постоянное манометрическое
давление рм=2,2 атм, под действием
которого вода по трубопроводу диаметромd=25 мм вытекает в емкость
В. Определить расход воды в трубе, если
Н1=1 м, Н2=5 м, длина трубопроводаl=H2+1м,
а коэффициент сопротивления вентиля
вен=4,0.
Решение:
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно
плоскости сравнения
0-0:
Z1+
+
где Z1=H1;p1=pм+ра;V1
0;Z2=H2;p2=pатм;V2
0;
hn=
.
.
Тогда Н1-Н2+
=
.
Откуда найдем скорость воды Vв трубе:
V=
м/с,
где
,
т.е. считаем, что труба работает в
квадратичной зоне сопротивления:
.
Уточняем зону работы трубопровода. Для этого найдем число Рейнольдса:
Re=
.
По графику на рис 3.4 Альтшуля А.Д “Примеры расчета по гидравлике” уточняем, что труба работает в переходной зоне.
Тогда уточним коэффициент Дарси:
Погрешность при этом составит:
%=
%.
Уточняем скорость движения воды в трубе
V=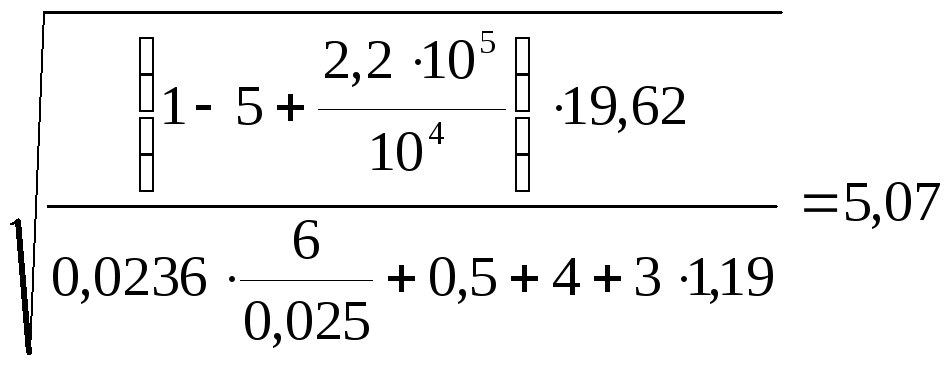
м/c.
Расход, протекающий по трубе, составит:
Q=V
=5,07
л/с.
Ответ:Q=2.49
м3/с.
3.23. В закрытом резервуаре поддерживается
постоянное манометрическое давление
,
под воздействием которого по новой
стальной трубе диаметромd=50мм
и длинами
вытекает
вода при температуре
.
Определить расход в трубе.
Указание. В первом приближении при
решении задачи следует принимать
квадратичную область сопротивления, а
затем уточнить значение
Решение:
С
оставим
уравнение Бернулли для сечений 1-1 и 2-2
относительно плоскости сравнения 0-0
(см. рис)
где
Найдём длину трубопровода:
Потери напора по длине и в местных сопротивлениях составят:
.
Уравнение Бернулли примет вид:
.
Найдём скоростной напор:
,
откуда определим скорость на выходе из трубы:
.
Предположим, что зона сопротивления – квадратичная, тогда коэффициент Дарси составит:
.
Найдём скорость в трубе:
где коэффициент сопротивления поворота:
(при
).
Найдём число Рейнольдса:
.
Так как число Рейнольдса оказалось
в диапазоне
<
<
,
то труба работает в переходной зоне.
Уточним коэффициент Дарси по формуле
Уточняем скорость в трубе:
.
Найдём расход:
.
Ответ: Q= 0,006 м3/с.
3.24. В бак подается вода с постоянным расходомQ, а чтобы избежать переполнения бака, установлена сливная труба диаметромd= 125 мм и общей длиной 8 м с коэффициентом трения λ = 0,025. Определить при каком напореHрасходы притока и истечения воды из бака составятQ= 25 л/с, если радиус закругления поворотов трубыR= 20 см, а значениеh= 7 м.
Решение:
Составим уравнение Бернулли для
сечений 1-1 и 2-2 относительно плоскости
сравнения 0-0 (см. рис.)
где
– примем дляпервого
приближения: 
,так как площадь
бака много больше площади трубы;
Tогда:
Где
Скорость в трубе
составит: 
.
Тогда потери напора по длине:
.
Потери на вход составят:
где
(табл. П-28).
Найдём потери на вход:
.
Потери на поворот:
где
- коэффициент на поворот.
Находим
,
величина коэффициента составляет
.
Тогда потери напора
.
Вычислим
.
Общие потери составят:
.
Найдем напор Н:
Знак «минус» указывает на то, что при заданном расходе, диаметре трубы, малых сопротивлениях и т.д. уровень в баке упадёт до уровня сечения входа в трубу, т.к. расход оттока будет больше расхода притока и установится некоторый безнапорный излив через трубу.
3.25. Ось горизонтального участка трубы AB расположена на высоте h1=0,35 м над уровнем воды в резервуаре M. Длины и диаметры участков соответственноl1=35м, d1=70 мм,l2=14 м, d2=135 мм, коэффициенты потерь в закруглениях ζ=0,15 и коэффициенты трения λ=0,03. Определить напор H, при котором давление в сечении 1–1, отстоящем от начала трубопровода AB на расстоянииl=10 м достигнет р1=2,2 Н/см2.
Решение:
Составим уравнение Бернулли для сечений I-IиII-II, относительно плоскости сравнения 0-0 (см.рис.):
где ZI= H + h1;ZII=0;pI=pII= Pатм;
V1=VII≈ 0.
Тогда H + h1= hw,
где hw- потери напора в местных сопротивлениях и по длине трубопровода:
hw=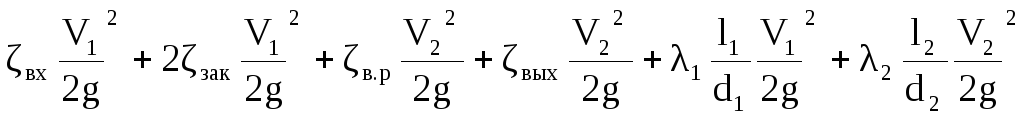
.
Выразим скорость V2 через скоростьV1, используя уравнение постоянства расхода:
V2=V1
.
Подставим значение в уравнение Бернулли:
Н+h1=
=
,
где
;
;
;
.
Подставляя все значения и преобразовывая, получим:
H=0,92
.
(
)
Запишем теперь
уравнение Бернулли для сечений I-Iи 1-1, относительно плоскости сравнения
,
проходящей через ось участка трубы АВ:
,
где ZI=H;Z1=0;
VI=0;pI=pатм;
Тогда H+
.
Подставляя значения, и учитывая, что
р1-это избыточное давление, получим:
Н=
.
Решая это
уравнение совместно с (
),
получим:
.
Откуда найдем скорость на первом участке трубы:
V
,
следовательноV
м/с, из системы уравнений найдем напор
Н:
Н=0,92
м.
Ответ: Н=3,4 м.
3.26. И
з
реки в колодец поступает вода с расходомQ=60 л/с по трубе диаметромd=150 мм и длиннойL=100
м. На входе в трубу расположена сетка с
обратным клапаном. Определить разность
уровней воды в реке и в колодце, если
коэффициент трения трубы λ=0,022.
Решение:
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнений 0-0 (см. рис.):
,
где z1
=H;P1=P2=Pатм;z2=0;
;
.
Потери напора равны
=h
+hм=
.
Подставим эти значения в уравнение Бернулли
H=
.
Вычислим скорость воды в трубе
=
=3,397м/с
3,4м/с.
По справочным данным найдём значения коэффициентов
Подставим все значения в уравнение и найдём разность уровней воды
H=0,5
=15,41м.
Ответ. Н=15,41м.
3.27. При
проведении опытов со стальной трубой
диаметромd=32мм установлено,
что закон гидравлического сопротивления
– квадратичная зона, а коэффициент
Дарси
.
Определить эквивалентную шероховатость
трубы.
Решение:
Используем
формулу Шифринсона для нахождения
коэффициента
;
.
Ответ:
.
3.28.Недалеко от конца трубопровода диаметромd=0,15 м, транспортирующего вязкую жидкость (ρ=900кг/м3, ν=1·10-4м2/с), имеется задвижка Лудло. Определить пьезометрическое давление перед задвижкой при расходеQ=0,04 м3/с, если степень открытия задвижкиn=0,75. В конце трубопровода давление равно атмосферному.
Решение. Находим скорость течения жидкости в трубе:
Число Рейнольдса, характеризующее течение в трубопроводе,
Определяем коэффициент сопротивления по формуле:
По табл. П-23 находим значение А=350, ζкв=0,2. Тогда
Потери давления найдем по формуле:
Учитывая, что в конце трубопровода избыточное давление отсутствует, пьезометрическое давление перед задвижкой будет равно 710 Па.
Ответ: 
3.29.Горизонтальная труба диаметромd1=0,1 м внезапно переходит в трубу диаметромd2=0,15 м. Проходящий расход водыQ=0,03 м3/с. Требуется определить: а) потери напора при внезапном расширении трубы; б) разность давлений в обеих трубах; в) потери напора и разность давлений для случая, когда вода будет течь в противоположном направлении (т.е. из широкой трубы в узкую); г) разность давлений при постепенном расширении трубы (считая потери напора пренебрежимо малыми).
Решение.а) Находим потери напора при внезапном расширении трубопровода по формуле Борда:
б) Находим разность давлений в узкой и широкой трубах из уравнения Бернулли:
или
в) При изменении направления движения на обратное, т.е. из широкой трубы в узкую, скорость в сжатом сечении
Степень сжатия потока
Коэффициент сжатия трубы найдем по формуле
Разность давлений
г) Если бы был обеспечен плавный переход от трубы узкого сечения к трубе широкого сечения, то разность давлений была бы равна:
Ответ: а)
;
б)
;
в)
;
г)
.
3
.30.Определить потери давления при движении
масла в радиаторе, если расход маслаQ=2·10-4м3/с.
Диаметр коллектора радиатораd0=0,03
м, диаметр трубокdтр=0,01
м, длина ихlтр=1 м.
Плотность масла ρ=900кг/м3,
кинематическая вязкость ν=6,5·10-5м2/с.
Решение.Скорость течения масла в коллекторах
Найдем потери давления в трубках по длине и потери на местные сопротивления. Все четыре трубки находятся в одинаковых условиях. Следовательно, расход в каждой из них
Скорость течения масла в трубке
Число Рейнольдса
Таким образом, течение в трубках ламинарное. Потери давления по длине находим по формуле Пуазейля:
Потери давления в местных сопротивлений определяем по формуле Вейсбаха:
Коэффициент местных сопротивлений вычисляем по формуле:
По табл. П-23 находим для входа в трубки: ζвх.кв=0,5 и А=30; для выхода из трубок ζвых.кв=1 и А=30. Подставляя найденные значения, получаем:
ζвых=30/97+1=1,3; ζвх=30/97+0,5=0,8.
Тогда
Общие потери давления при движении масла в радиаторе
Ответ: 
3.31 . Из резервуара вытекает вода по трубопроводу переменного сечения, размеры которогоl1=10 м ,l2=50 м ,d1=7,5 см,d2=10 см,H=2.0 м. Определить показания ртутного манометра при известном расходеQ=10 л/с.
Решение:
Составим уравнение Бернулли для сечения 1-1 и 2-2 относительно плоскости сравнения
(см.рис.): Z1+
+
=Z2+
+
+
+hw
,
где Z1=H;p
=pм
;V1=0 ;Z2=0;p
=pатм;V2=
.
Потери напора состоят из потерь напора по длине и в местных сопротивлениях:
h
=h
+hм=h
+h
+h
+h
Тогда уравнение Бернулли принимает вид:
H+
=
+
+
+
+
.
Найдем скорости в трубах:
V
=
=
=2,26
м/с;
V
=
=
=1,27
м/с.
Найдем числа Рейнольдса:
R
=
=
=167822;
R
=
=
=125743.
По рисунку 4-2а (Киселев П.Г Справочник по гидравлическим расчетам) видно, что этим
значениям чисел Рейнольдса соответствует переходная зона сопротивления. Коэффициенты Дарси найдем по формуле А.Д.Альтшуля:
,
где K
=0,014
мм – примем как для стальных труб новых,
чистых.
Тогда:
;
.
Тогда потери по длине составят:
h
0,0172
=0,6+0,73=1,33 м.
Найдем потери напора на входе:
h
,
где
( стр 48 Киселев П.Г Справочник по
гидравлическим расчетам).
h
м.
Потери напора при внезапном расширении:
h
;
;
h
м.
Окончательно получим уравнение:
H+
,
откуда:
м,
т.е на свободной поверхности будет вакуум.
p
h=
0,007
мм рт.ст.
Если же предположить, что труба старая,
ржавая, то К
можно принять равным К
=1
мм.
Тогда в этом случае:
;
.
Потери напора по длине при этом составят:
h
м,
Местные потери напора:
h
м;h
м.
Тогда
м.
В этом случае показание hбудет составлятьp
,
откуда найдем показания манометра:
h=
=
м =63 мм рт.ст.
Таким образом давление над свободной поверхностью воды в резервуаре должно быть больше атмосферного.
Ответ:h=63 мм рт.ст.
3.32. Насос забирает из водоема воду с температурой 200С в количествеQ=50 л/с. Определить максимальную высоту расположения горизонтального вала насоса над свободной поверхностью водыH1, если давление перед насосомp2=0,3·105Па. На всасывающей чугунной трубе диаметромd=0,25 м и длинойl=50 м имеется заборная сетка, плавный поворот радиусомR=0,5 м и регулирующая задвижка, открытая на 45% площади проходного сечения.
Решение.Запишем уравнение Бернулли для двух сечений 1-1 (по уровню свободной поверхности водоема) и 2-2 (перед насосом):
где V1 – средняя скорость течения воды на свободной поверхности водоема;
p1– атмосферное давление;
V2 – средняя скорость течения воды во всасывающей трубе;
Δpпот – сумма потерь давления по длине и местных потерь.
Учитывая, что z1=0,V1≈0, и принимая плоскость 1-1 в качестве плоскости сравнения, находим:
Высота расположения насоса над уровнем воды в водоеме
Средняя скорость течения воды во всасывающей трубе
Суммарные потери давления
где ∑ζ=ζзаб+ζпов+ζв
Здесь ζзаб=5 (см. табл. П-28) – коэффициент местного сопротивления на вход во всасывающую трубу;
ζпов– коэффициент местного сопротивления на плавный поворот трубопровод;
ζв=5 – коэффициент местного сопротивления задвижки [9; табл. 4.21].
Число Рейнольдса (при ν=1,01·10-6 м2/с; см. табл. П-12)
Для чугунных труб kэ=1 мм [7; табл. 3.1]
По рис. 3.1 находим, что всасывающий трубопровод работает в квадратичной зоне сопротивления. Коэффициент гидравлического трения определяем по формуле Шифринсона:
Коэффициент местного сопротивления на плавный поворот ζпов вычисляем по формуле:
Суммарные потери давления при плотности воды ρ=998,2 кг/м3:
Тогда
Высота расположения насоса не должна превышать 6,2 м.
Ответ: 
3.33. Расход горячей воды с температурой 950С через радиатор водяного отопленияQ=0,1 м3/ч. Определить потери давления между сечениями 1-1 и 2-2, если диаметр подводящих трубопроводовd=0,0125 м, а общая их длинаl=5 м.
Решение.Суммарные потери давления
где Δpл– потери давления по длине;
Δpм – местные потери.
Средняя скорость течения воды в трубопроводе:
Число Рейнольдса (при ν=1,01·10-6 м2/с; см. табл. П-12)
Абсолютная шероховатость стальной трубыkэ=5·10-5м (табл. П-15), относительная шероховатость
По графику зон гидравлического сопротивления (рис.3.1) находим, что трубопроводы работают в переходной зоне сопротивления. Коэффициент гидравлического трения определяем по формуле Альтшуля:
Потери давления по длине при плотности воды ρ=961,32 кг/м3(см. табл. П-4)
Местные потери давления складываются из потерь на поворот, в пробковом кране и в радиаторе. Для поворота ζ90о =1,4; для крана ζкв=0,4 (см. табл. П-23); для радиатора ζр=2 (см. табл. П-28). Эти значения коэффициентов местных сопротивлений рекомендованы для зоны квадратичного сопротивления, т.е. для больших чисел Рейнольдса. Влияние числа Рейнольдса на местные сопротивления учитываем по формуле
Из табл. П-23 имеем для поворота под углом 900A=400, для пробкового кранаA=150. Для радиатора приближено принимаемA=500ζр=500·2=1000.
Сумма коэффициентов местных сопротивлений
Потери давления на местные сопротивления
.
Суммарные потери давления
Ответ:
3.34.Насос с подачейQ=0,01 м3/с забирает воду из колодца, сообщающегося с водоемом чугунной трубой диаметромd=150 мм и длинойl=100 м. На входе в трубу установлена сетка. Температура воды в водоеме 200С. Найти перепад уровней воды Δhв водоеме и колодце.
Решение. Запишем уравнение Бернулли для двух сечений 1-1 и 2-2, принимая уровень воды в колодце 2-2 за плоскость сравнения:
Учитывая, что p1=p2 иV1≈V2≈0, получаем:
Потери давления в трубе
Скорость течения жидкости в трубе
Число Рейнольдса (при ν=1,01·10-6м2/с; см. табл. П-12)
Абсолютная шероховатость чугунной трубы [7; табл. 3.1] kэ=1 мм=10-3м. Относительная шероховатость
По графику зон гидравлического сопротивления (рис.3.1) находим, что труба работает в квадратичной зоне сопротивления. Коэффициент гидравлического трения вычисляем по формуле Шифринсона:
Местные потери давления складываются из потерь давления на вход в трубу и на выход из нее: ζвх=6 (табл. П-28), ζвых=1.
Перепад уровней воды в водоеме и колодце
Ответ: 
3.35.Сифонный бетонный водосброс диаметромd=1 м, общей длинойl=50 м сбрасывает воду из водохранилища в реку, уровень которой наH=5 м ниже уровня водохранилища. Определить подачуQсифонного водосброса, если он имеет два поворота: α=900 и α=450 с радиусами закругленияR=2 м. Длина горизонтального участкаlr=2 м, толщина стенок водосброса δ=0,05 м. Температура воды в водохранилище 00С. Определить также вакуумpвакв верхней точке сифона, еслиz1=1 м,z2=3 м.
Решение.Разность уровней воды в водохранилище и реке определяет суммарные потери давления в сифонной трубе:
Потери давления состоят из потерь по длине и в местных сопротивлениях
Скорость движения воды в сифонном водосбросе
Примем первоначально, что водосброс работает в квадратичной области сопротивления. Тогда по формуле Шифринсона при kэ=5·10-4м[7;табл. 3.1]
Коэффициент местного сопротивления на вход в трубу (при δ/d=0,05/1=0,05) ζвх=0,5. Коэффициент сопротивления на поворот 900находим по формуле:
Коэффициент сопротивления на поворот
450определяем по формуле:
,
принимая а=0,7 , получим ζ45о=
ζ90.а=0,18·0,7≈0,13. Коэффициент
сопротивления на выход из трубы ζвых=1.
Сумма коэффициентов местных сопротивлений
Скорость в сифоне
Число Рейнольдса при ν=1,79·10-6м2/с; (см. табл. П-12)
При
по рис. 3.1 устанавливаем, что водосброс работает в квадратичной области сопротивления.
Расход воды через сифонный водосброс
Составим уравнение Бернулли для сечений 1-1 и 2-2:
Потери давления на участке 1-2
где l1=z2+lr=3+2=5 м и ρ=999,9кг/м3(см. табл. П-4).
Подставляем численные значения и получаем:
Величина вакуума в верхней точке водосброса
Ответ: 
;
.
3.36.В стальном трубопроводе системы горячего водоснабжения диаметромd=0,0125 м, длинойl=100 м движется вода со скоростьюV=0,5 м/с. Температура воды 500С. На трубопроводе имеются два поворота под углом α=900и пробковый кран. Определить потери давления и сравнить их с результатами расчета, выполненного в предположении квадратичного закона сопротивления.
Решение.Суммарные потери давления Δpпот складываются из потерь на трение по длине Δpл и потерь в местных сопротивлениях Δpм.
Число Рейнольдса (при ν=0,55·10-6м2/с; см. табл. П-12)
Для стального трубопровода kэ=5·10-5(см. табл. П-15); относительная шероховатость
kэ/d=5·10-5/0,0125=4·10-3.
По рис. 3.1 устанавливаем, что трубопровод работает в переходной области сопротивления. Коэффициент гидравлического трения находим по формуле Альтшуля:
Потери давления на трение по длине трубопровода ρ=988,1 кг/м3(см. табл. П-4)
Коэффициент местных сопротивлений определяем по формуле:
для поворота под углом 900ζкв=1,4; А=400 (см. табл. П-23);
для пробкового крана ζкв=0,4; А=150 (см. табл. П-23).
Сумма коэффициентов местных сопротивлений
Местные потери давления
Суммарные потери давления
Если считать, что трубопровод работает в области квадратичного сопротивления, то по формуле Шифринсона найдем коэффициент Дарси
а потери давления составят:
Таким образом, потери давления, рассчитанные в предположении квадратичного закона сопротивления, будут занижены против реальных потерь на 14%.
Ответ: 
;
.
3.37.Найти потери давления Δpм на преодоление местных сопротивлений при движении воды в стальном трубопроводе диаметромd=0,025 м при повороте на угол 90°без вставки и с вставкой. Найти наименьшую длину вставкиlвл, при которой отсутствует взаимное влияние двух местных сопротивлений. Скорость водыV=5 м/с, температура воды 20°С.
Решение.Потери давления при повороте на угол 90°без вставки (а) и со вставкой (б) находим по формуле:
и
Принимая ν=1,01·10-6м2/с (см. табл. П-12), находим число Рейнольдса для потока воды в трубе:
Относительная шероховатость при kэ=5·10-5м (см. табл. П-15)
Коэффициент гидравлического трения трубопровода найдем по формуле Альтшуля:
Коэффициент местного сопротивления при резком повороте на 90°(см. табл. П-20) ζ90°=1,3. Коэффициент местного сопротивления при резком повороте на 135°находим по формуле
Два поворота под углом α=135°не влияют друг на друга, если расстояние между ними больше, чемlвл. По формуле определяем длину влияния
Отсюда
Таким образом, если расстояние между двумя поворотами α=135°больше, чемlвл=0,65 м, то местные сопротивления не будут оказывать влияние друг на друга. В этом случае
Вставка может снизить потери давления в 4 раза.
3.38. Из напорного бакаАс отметкой
горизонта воды 15,50мтребуется подать
в пунктВводу на отметку 10,6мв
количествеQ= 20,6л/с.
Между пунктамиАиВрасстояниеl= 880м. Для прокладки
водопровода имеются «нормальные» трубы
с диаметрами
(вес 1пог. м38 кг, или 372,8Н) и
(вес
1пог. м55 кг, или 539,6Н). Какие
трубы надо поставить, чтобы их общий
вес был наименьшим?
Решение.Определим при заданном
напоре
расходную характеристику
.
По табл. П-16 находим
для
и
для
.
Из сопоставления табличных значений
Kс расчетным следует,
что при постановке труб
не обеспечится пропуск заданного расхода
при расчетных отметках, а при
пойдет расход больше расчетного или
останется излишний напор.
Проектирование труб с
по всей длинеАВповедет к излишней
затрате металла. Для обеспечения
расчетных условий при наименьшей затрате
металла составим трубопровод из двух
последовательно соединенных участков
одного и другого диаметров.
Сумма потерь напора на обоих участках
.
При
скорость в трубопроводе
.
Область сопротивления квадратичная,
так как скорость
большеV, указанной в
[4; табл.VI] для нормальных
труб
.
При
скорость
.
Область сопротивления переходная, так
как скорость
меньше указанной в [4; табл.VII]
для труб
.
Обозначая черезxдлину (в километрах) участка с диаметром
,
будем иметь сумму потерь напора во всей
длине трубопровода:
.
Подставив числовые значения,
воспользовавшись [4; табл. VI],
получим
и найдем отсюда
.
Вес труб с
на участкеxсоставит
,
или
.
На остальной длине
вес будет
,
или
Общий вес труб
,
или
.
Это будет наименьший вес при условии
использования заданного напора.
Ответ:
.
3.39. От напорного бакаАв пунктВпроложены два параллельных
трубопровода. В одном из трубопроводов
расход распределяется в виде непрерывной
раздачи
.
В пунктВпоступает транзитный
расход
на отметку
.
Горизонт воды в напорном баке А расположен
на отметке
.
Трубы нормальные.
Определить:
Транзитный расход
в пунктеВ.Отметку горизонта воды в напорном баке А, обеспечивающую увеличение расхода
в 2 раза (при этом расход
и отметка пьезометрической линии в
пункте В остаются без изменения).
Решение.1) Расход в первом трубопроводе (без раздачи) определится по формуле:
,
г
де
[4; табл.V] для диаметраd=150мм.
Этот расход целиком поступает в
водоразборный пункт В. Однако полный
расход
может быть больше, чем
,
так как во втором трубопроводе, кроме
непрерывной раздачи
,
возможно наличие транзитного расхода
.
Определим расход
во втором трубопроводе из формулы
.
Отсюда
.
Подставляя числовые значения, получим:
.
Решая уравнение, находим
.
Следовательно, полный расход в пункте Вбудет:
.
2) Расход в пункте Вувеличен вдвое, т. е.
.
Определим, при каком напоре будет
обеспечен этот расход. Потери напора в
обоих (параллельных) трубопроводах
одинаковы. Следовательно, можно написать
равенство, полагая расход в первом
трубопроводе
,
,
или
.
Подставляя численные значения, получим:
.
Решая уравнение, найдем
.
Следовательно, расход в первом трубопроводе
.
Потери напора при этом
.
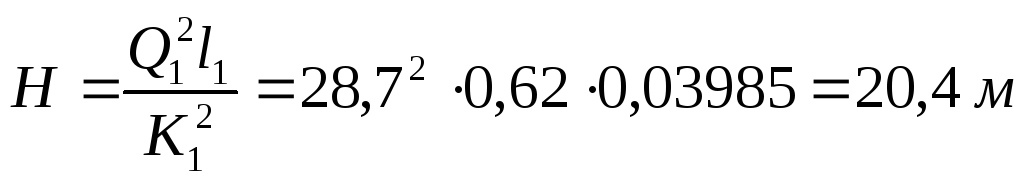Отметка горизонта воды в бака Адолжна быть:
.
3.40. Определить, какой расход можно перекачать сифоном из водоема А водоем В при разности горизонтов Н=1,5м, если длина сифонаl=75м, а диаметр сифонаd=200мм. Трубы чугунные, нормальные (Δ=1,35мм). Вычислениями выяснить, будет ли в сечениях 1-1, 2-2, 3-3, 4-4, 5-5 манометрическое давление или вакуум. Найти, где расположены сечения, в которых давление в сифоне будет равно атмосферному. Почему в сечении 3-3 будет наибольший вакуум?
При расчете скоростными напорами в
водоемах пренебречь. Наибольшее
превышение над уровнем воды в водоеме
принять s=2м, а глубины
погружения
и
.
Температура воды
.
Решение. Составим уравнение Бернулли для сечений Ι-Ι, ΙΙ-ΙΙ, расположенных на свободной поверхности, приняв за плоскость сравнения сечение ΙΙ-ΙΙ (плоскость 0-0)
откуда
,
т. е. весь напор затрачивается на
преодоление сопротивлений.
Подставляем последовательно местные потери и потери по длине в уравнение:
.
Коэффициент потерь сетки с обратным
клапаном принимаем
(табл. П-28).
Для определения коэффициента потерь по длине λ необходимо знать режим движения. Так как в задаче требуется определить расход, то скорость неизвестна. Предполагаем, что движение происходит в квадратичной зоне, и находим коэффициент С по одной из формул, например по формуле Агроскина, приняв для нормальных труб k=4,04,
,
где
.
Тогда найдем коэффициент Дарси из формулы
.
По табл. П-28 при
находим
.
Потери на выход из трубы найдем по
формуле Борда-Карно
.
и, следовательно, в формуле Вейсбаха
примем
.
Подставляя числовые значения в исходное
уравнение, получим:
.
Найдем скорость в сифоне
.
Проверим режим движения, принимая
кинематический коэффициент вязкости
для воды
при температуре
,
.
Определяем нижнюю границу квадратичной области по формуле
.
Так как в рассматриваемом случае
,
то движение будет происходить в
квадратичной области и наше предположение
оказалось правильным. В противном случае
нужно было бы уточнить λ и пересчитать
скорость.
Расход определяем по формуле
где
.
Определим теперь, будет ли в сечении 1-1 манометрическое давление или вакуум. Составим уравнение Бернулли для сечения Ι-Ι, расположенного на свободной поверхности водоема и для произвольно выбранного сечения х - х, взятого внутри трубы. За плоскость сравнения выбираем сечение 1-1.
Тогда уравнение Бернулли запишем в виде:
,
где
-
расстояние от сеченияI-Iдо выбранного сечения;
- давление в выбранном сечении;
- пьезометрическая высота, соответствующая
полному давлению;
- потери напора до выбранного сечения.
Из уравнения Бернулли найдем
.
Из анализа этого уравнения видно, что
в сечениях, расположенных между 1-1 и
2-2, давление в сифоне будет манометрическим
до тех пор, пока
,
так как в этом случае
и
.
Если
,
то давление в сифоне будет равно
атмосферному, так как
и
.
Наконец, если
,
то
и в трубе будет вакуум
.
Расположив сечение
в сечении 1-1, получим:
В этом уравнении
и потери до сечения 1-1 равны
;
Следовательно, в сечении 1-1 давление
будет манометрическое:
.
Найдем, на каком расстоянии
,
расположено сечение
,
в котором давление будет равно
атмосферному. Это расстояние найдем из
условия, что
,
где
.
В этом уравнении неизвестным является
лишь расстояние
,
поэтому
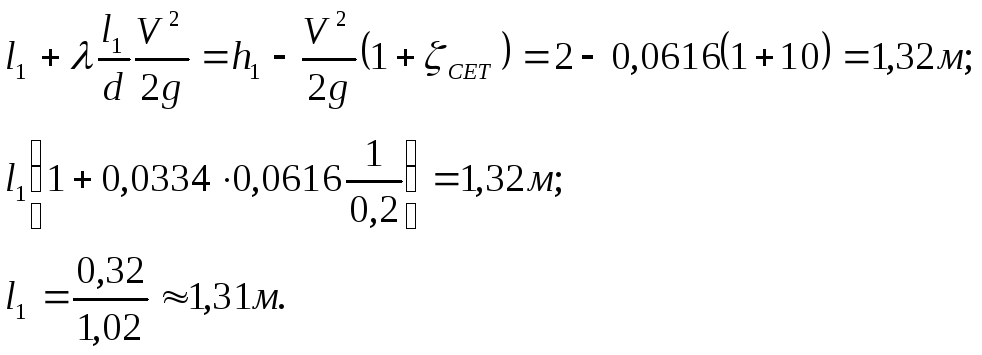
Определим давление в сечении 2-2, внутри трубы, по исходному уравнению Бернулли
или
т. е. в сечении 2-2 будет вакуум, величина которого равна
Найдем давление в сечении 3-3, считая
Таким образом, в сечении 3-3 будет вакуум
Найдем вакуум в сечении 4-4, считая (
),
т.е. в сечении 4-4 также будет вакуум
.
Сопоставляя вакуум в сечениях 2-2 и 4-4, замечаем, что вакуум в последнем сечении значительно превосходит вакуум в сечении 2-2, что объясняется увеличением потерь в сифоне по направлению течения жидкости. Уменьшение вакуума в сечении 4-4 по сравнению с сечением 3-3 объясняется уменьшением высоты zxнад плоскостью сравнения.
Определим давление в сечении 5-5. Чтобы упростить вычисления, составим уравнение Бернулли для произвольного сечения x`-x` и сечения
II-II, приняв за плоскость сравнения 0-0. Тогда
Принимая ζвых=1, после сокращения получим:
и
Так как в сечении 5-5 геометрическая
высота
=0,
то манометрическое давление найдем из
уравнения
т.е.
Следовательно, член
в сечении 5-5 будет превышать
на величину напора, затрачиваемого на
преодоление потерь по длине
.
Сечение, в котором давление в правой вертикальной части сифона будет равно атмосферному, найдем из условия
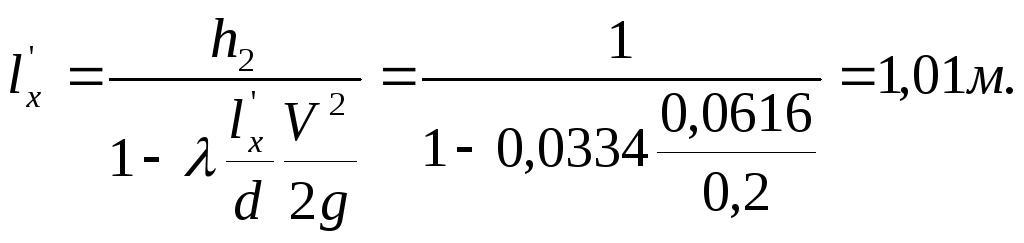
В сечении 3-3 вакуум будет наибольшим потому, что в этом сечении при наибольшей геометрической высоте zxпотери будут наибольшими. В сечениях, расположенных по течению ниже сечения 3-3, вакуум будет меньше, так как геометрическая высота уменьшается быстрее, чем нарастают потери по длине.
3.41. Из бака при постоянном напореН по прямому горизонтальному трубопроводу длинойlи диаметромd вытекает вода в атмосферу, а на расстоянииl1 от начала трубопровода установлен вентиль. Определить расход воды в трубопроводе при полном открытии вентиля и построить пьезометрическую и напорную линии, если
l = 100мм; l1
=80м; D
= 0,1м; Н = 5м;
= 0,03.
Решение:Составим уравнение Бернулли
для сечений0—0 и4—4
относительно плоскости сравнения
,
проведенной через ось трубы
В рассматриваемом случае z0=H;р0 = р4;
поскольку скорость движения воды в
баке несоизмеримо меньше скорости
движения воды в трубе, можно принять,
чтоV0
0,z4
=pa
,тогда
.
Подставив эти значения в уравнение Бернулли, получим
.
Так как
,
то
Учитывая, что
,
и решив последнее уравнение относительно
искомого расхода, получаем:
В данном случае сумма коэффициентов
потерь
местных сопротивлений складывается из
коэффициента потерь на вход в трубу
и коэффициента потерь в вентиле диаметром
D = 0,1м при
полном открытии
.
Таким образом, с учетом потерь по длине:
Подставляя известные величины в формулу для расхода, находим, что
Для построения пьезометрической
линии находим зависимость, по которой
можно определить величину пьезометрического
напора в любом сечении трубопроводов.
Для этого составим уравнение Бернулли
для сечения 0—0 и любого сечения
трубопроводах—х относительно
плоскости сравнения
.
или
Учитывая, что
и
,получаем
,
где
—
сумма коэффициентов потерь на участке
от сечения0—0 до сеченияx-x.
Из уравнения определим величину
пьезометрического напора в сечении 1—1
,
где
;
Определим величину пьезометрического
напора в сечении 2—2. Здесь
Далее определим величину пьезометрического напора в сечении 3 —3:
В сечении 4-4 имеют место равенства
и
Откладывая полученные значения величин
пьезометрических напоров в каждом
сечении от плоскости сравнения
,
строим пьезометрическую линию.
Поскольку напор в трубопроводе постоянного сечения равномерный, напорная линия будет параллельна пьезометрической и расположится выше последней на величину
Ответ: Q= 0,0128
.
3.42.Определить расход водыQприt = 15оС и полное давлениерв наивысшей точке сифонного нового стального трубопровода, если его диаметрd= 50мм; длинаl= 10м; разность уровней воды в резервуарахН= 1,2м; превышение наивысшей точки сифона над уровнем воды в первом резервуареh=1м, а расстояние от начала трубопровода до сечения 1—1 равно 3м.
Решение.Составим уравнение Бернулли для сечений0—0и2—2относительно плоскости сравнения, совмещенной с сечением0—0:
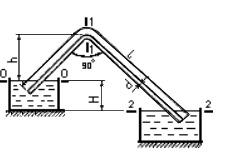
В условиях задачи
p0 = pa;
V0=0;
Таким образом, получим:
Откуда:
В полученной формуле сумма коэффициентов потерь:
Поскольку в общем случае
зависит от шероховатости трубы
и числа РейнольдсаRе,
которое при неизвестной скорости также
является неизвестным, в первом приближении
допускаем, что это квадратическая
область гидравлических сопротивлений,
где
По таблице П-15 для значений эквивалентной
шероховатости находим среднее
значение
для новых стальных цельнотянутых труб
0,06мм. Таким образом,
Следовательно,
тогда
.
Проверим принятую ранее область гидравлических сопротивлений.
или
Сравнив полученное число Рейнольдса с
величинами
и
,
найдем,
что 8330 < 96000 < 466480. Следовательно, поток находится в переходной области гидравлических сопротивлений, где коэффициент трения определяется по формуле А.Д. Альтшулля:
Далее находим новое значение:
Затем определяем
расход при найденном значении
:
.
Поскольку расхождение между расходами
невелико, величину
можно не уточнять.
Полное давление в сечении 1—1 найдем, составив уравнение Бернулли для сеченийО—О и1—1, совместив плоскость сравнения с сечениемO—О:
В рассматриваемом случае z0=0;
Тогда записанное выше уравнение примет вид
откуда
В данном случае
Таким образом,
или
кг/см2
Ответ:
3.43.Из резервуараА по новой чугунной трубе диаметром
d = 200мм вода приt= 15oС поступает в резервуарВ при напорахН1 = 4м иH3= 1м и длинах участковl1= 30м иl2= 50м. Определить:
напор H2в резервуареБ, если труба горизонтальна;
Решение.Составим уравнение Бернулли для сечений0 —0 и2 —2 относительно плоскости сравнения О1= О1, проведенной через горизонтальную ось трубы,
В рассматриваемом случае
где
и
— коэффициенты потерь местных
сопротивлений при входе и выходе из
резервуаров.
Таким образом,
откуда скорость движения воды в трубе
По таблице П-28 коэффициентов потерь
местных сопротивлений найдем
В первом приближении принимаем
квадратическую область гидравлических
сопротивлений и определяем коэффициент
Дарси по формуле Шифринсона
Приняв среднее значение эквивалентной
шероховатости для новых чугунных
труб
= 0,62мм, получим
Следовательно,
дм/с = 2,05м/с
Для уточнения коэффициента Дарси
определим число Рейнольдса
при кинематическом коэффициенте вязкости
для воды приt =
15°C,
= 0,0115см2/с, откуда
Определяя соотношение
устанавливаем, что поскольку
то область гидравлических сопротивлений
выбрана верно и пересчета значений
делать не следует.
Для определения напора H2составим уравнение Бернулли для сеченийО—О и1—1относительно той же плоскости сравнения. Руководствуясь изложенным выше, получаем
откуда
м.
Ответ:H2=2,84 м.
3.44. По вытяжной трубе диаметромD= 700мм газ удаляется из борова
котельной установки, где имеется
разрежение, соответствующее высоте 10мм вод. ст. Плотность газа
г=0,07кг/м3; плотность
воздуха
=1,2кг/м3;
отношение сечения борова к сечению
трубы
1/
2= 2. Гидравлический коэффициент трения
= 0,02; коэффициент потерь на входе в трубу
с поворотом
= 0,7. Определить: необходимую высоту
трубыН для создания тяги, если
весовой расход дымовых газов М = 8000
кг/ч=78,45кН/ч;
Решение.Определим скорость газа в трубе
м/с.
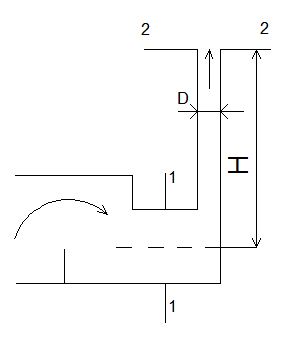
Выбрав плоскость сравнения по оси борова, напишем уравнение Бернулли для сечений 1—1 и2—2
и уравнение изменения атмосферного давления по высоте
Решив совместно эти уравнения с учетом того, что
получим
или
Ответ:Н= 31,1м.