
- •1. Физические свойства жидкости
- •Примеры
- •2. Гидростатика
- •2.1. Гидростатическое давление
- •Примеры
- •2.2. Сила гидростатического давления на плоскую поверхность
- •Примеры
- •2.3. Сила гидростатического давления на криволинейную поверхность
- •Примеры
- •2.4. Плавание тел
- •Примеры
- •3. Уравнение д. Бернулли
- •3.1. Уравнение д. Бернулли без учета потерь энергии
- •Примеры
- •3.2. Уравнение д. Бернулли с учетом потерь энергии
- •Примеры
- •4.Истечение жидкости из отверстий и насадков
- •4.1. Истечение жидкости из отверстий
- •4.2 Истечение жидкости из насадков
- •Примеры
3. Уравнение д. Бернулли
3.1. Уравнение д. Бернулли без учета потерь энергии
Уравнение Д. Бернулли для потока невязкой жидкости (без учета потерь энергии), составленное в отношении произвольно выбранной плоскости сравнения, имеет следующий вид:
![]()
Левая часть уравнения представляет
собой сумму двух видов энергии:
потенциальной, состоящей из энергии
положения
![]() и энергии давления
и энергии давления![]() ,
и кинетической энергии
,
и кинетической энергии![]() ,
отнесенных к единице веса движущейся
жидкости. Коэффициент кинетической
энергии потока
,
отнесенных к единице веса движущейся
жидкости. Коэффициент кинетической
энергии потока![]() ,
входящий в уравнение Д. Бернулли при
движении невязкой жидкости, может
быть принят равным единице.
,
входящий в уравнение Д. Бернулли при
движении невязкой жидкости, может
быть принят равным единице.
Многие практические задачи, связанные с установившимся движением жидкости, решаются совместным применением уравнения Д. Бернулли и уравнения неразрывности (сплошности) потока.
Уравнение неразрывности может быть записано в следующем виде:
![]()
откуда
![]()
![]()
где V1иV2— средние скорости в сечениях потока;
![]() и
и![]() — соответствующие площади живых сечений.
— соответствующие площади живых сечений.
Примеры
3.1.Определить расход воды![]() в трубе диаметром
в трубе диаметром![]() ,
имеющей плавное сужение до диаметра
,
имеющей плавное сужение до диаметра![]() ,
если показания пьезометров: до сужения
,
если показания пьезометров: до сужения![]() ;
в сужении
;
в сужении![]() .
Температура воды
.
Температура воды![]() .
.

Решение.Составим уравнение Бернулли для сечений 1-1 и 2-2, принимая за плоскость сравнения ось трубы:
![]() .
.
Учитывая, что
![]() ,
пренебрегая потерями напора, т. е.
принимая
,
пренебрегая потерями напора, т. е.
принимая![]() ,
и полагая
,
и полагая![]() ,получим:
,получим:
![]() .
.
Из уравнения неразрывности расхода имеем:
![]() .
.
Поскольку
![]() ;
;![]() ,
,
находим:
![]() .
.
Обозначим
![]() .
.
Тогда уравнение Бернулли запишется в виде
 ,
,
откуда найдем скорость в сечении 1-1:
 .
.
Расход воды в трубе
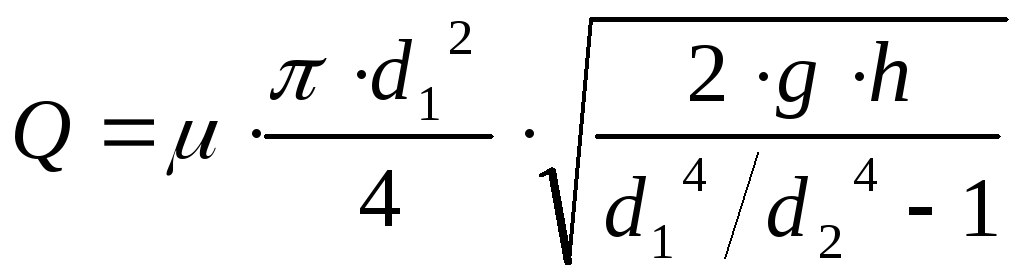 ,
,
где μ – коэффициент, учитывающий уменьшение расхода вследствие потерь напора; в первом приближении принимаем μ=0,98; тогда расход будет
![]() .
.
Коэффициент μ зависит от отношения
диаметров
![]() и числа Рейнольдса:
и числа Рейнольдса:
![]() ;
;
![]() .
.
Найдем скорость в сужении трубы
![]() .
.
Кинематическую вязкость воды примем:
![]() (табл. П-12).
(табл. П-12).
С учётом полученных данных найдем число Рейнольдса
![]() .
.
По табл. П-25 находим μ =0,98. Следовательно, в первом приближении значение μ принято верно.
Искомый расход
![]() .
.
Замечание: Рассмотренное сужение трубы с плавными переходами от большего диаметра к малому и от малого к большому называется водомером Вентури.
Ответ: ![]() .
.
3.2.Определить, на какую высоту
поднимается вода в трубке, один конец
которой присоединён к суженному сечению
трубопровода, а другой конец опущен в
воду. Расход воды в трубе![]() ,
избыточное давление
,
избыточное давление![]()
![]() ,
диаметры
,
диаметры![]() и
и![]() .
.
Решение.Уравнение Бернулли для
сечений 1-1 и 2-2 относительно оси трубы
(потерями напора пренебрегаем) имеет
вид (при![]() )
)
![]() .
.
Учитывая, что скорости в сечениях 1-1 и 2-2 находятся так
![]() и
и![]() ,
,
то после преобразований получим:


Полученная отрицательная высота –
вакуумметрическая высота. На эту высоту
![]() и поднимается вода в трубке.
и поднимается вода в трубке.
Ответ: ![]() .
.
3.3. Определить критическую скорость, отвечающую переходу от ламинарного режима к турбулентному, в трубе диаметромd= 0,03 м при движении воды и воздуха при температуре 25˚C и глицерина при температуре 20˚C.
Решение.Из формулы для критического числа Рейнольдса имеем:
![]() .
.
Для воды
![]()
![]() .
.
Для воздуха
![]()
![]() .
.
Для глицерина
![]()
![]() .
.
3.4. Определить давлениер1 в сечении1-1горизонтально расположенного сопла гидромонитора, необходимое для придания скорости водеV2 = 40м/св выходном сечении2-2, если скорость движения воды в сечении1-1 V1= 3м/с.

Решение.Данная задача может быть решена при помощи уравнения Д. Бернулли и уравнения неразрывности.
При составлении уравнения Д. Бернулли следует выбрать два сечения в рассматриваемом потоке и плоскость сравнения, по отношению к которой записывается уравнение для двух выбранных сечений. Эти сечения и плоскость сравнения выбираются так, чтобы наибольшее количество величин, входящих в уравнение, были известными, а в уравнение входили искомые величины.
При решении данной задачи удобно использовать сечения 1 — 1 и2 —2, поскольку скорости в этих сечениях заданы, давлениеp1подлежит определению, а давлениер2в сечении на выходе из гидромонитора равно атмосферному. Плоскость сравнения следует провести через ось сопла, тогда удельные энергии положенияz1 = z2 = 0 и уравнение Д. Бернулли будет иметь следующий вид:
![]()
откуда![]() .
.
О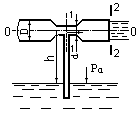 твет:
твет:![]() .
.
3.5.Определить диаметрdсуженной части горизонтального трубопровода, при котором вода поднимается на высотуh = 3,5м при расходе
Q= 6л/с и диаметреD = 10см.
Решение.Плоскость сравнения совместим с осью трубы. Выбрав сечения1 — 1 и2 —2 и составив уравнение Д. Бернулли, получим:
![]()
Так как плоскость сравнения проведена по оси трубы, то z1 =z2= 0, и тогда
![]()
Для того чтобы вода поднялась на высоту
3,5 м, необходимо, чтобы удельная
энергия давления в сечении1 — 1была
равна![]() ,
откуда
,
откуда![]() .
.
Так как истечение происходит в атмосферу, то давление р2равно атмосферному, т.е.
![]()
Следовательно,
![]()
Для определения диаметра суженной части
воспользуемся уравнением неразрывности
движения
![]() ,
где
,
где![]() и
и![]() .
.![]()
Подставив в уравнение найденные величины, получим
![]()
откуда искомый диаметр

Ответ:
![]() .
.
3.6.Определить расход воды в горизонтальном трубопроводе переменного сечения, скорость на каждом из участков и построить пьезометрическую линию, еслиH= 5м, d1= 15мм, d2= 20мм и d3 = 10мм.

Решение.Уравнение Д. Бернулли для сечений0 — 0 и3 —3при совмещении плоскости сравнения с осью трубы будет иметь вид
![]()
В данном случае
![]() =H,
=H,![]() = 0. В связи с тем, что в сечениях0—0
и3—3давление равно атмосферному,
то
= 0. В связи с тем, что в сечениях0—0
и3—3давление равно атмосферному,
то![]() .
Учитывая, чтоH=const,
а скорость в сечении0—0 V0= 0, скорость в выходном сечении3 —3определится из зависимости
.
Учитывая, чтоH=const,
а скорость в сечении0—0 V0= 0, скорость в выходном сечении3 —3определится из зависимости
![]()
откуда
![]()
Расход воды в трубопроводе
![]()
Скорость в сечении 1 — 1
![]()
Скорость в сечении 2 —2
![]()
Пьезометрическую линию строят, исходя
из следующих положений. Поскольку задача
решается без учета потерь энергии, то
напорная линия (линия полной энергии)
будет представлять собой горизонтальную
прямую, являющуюся продолжением свободной
поверхности воды в сечении 0 —0.
Пьезометрическая линия расположится
ниже напорной линии на величину![]() в каждом сечении. Таким образом, отложив
вниз от напорной линии величины
в каждом сечении. Таким образом, отложив
вниз от напорной линии величины![]() в сечениях, соответствующих изменению
диаметра трубопровода, получим ряд
точек, соединив которые построим
пьезометрическую линию (см. рис). При
этом:
в сечениях, соответствующих изменению
диаметра трубопровода, получим ряд
точек, соединив которые построим
пьезометрическую линию (см. рис). При
этом:
![]()
Ответ:
![]() .
.
3.7. Определить избыточное давление воды на входе в брандспойт и диаметр выходного сечения , необходимые для получения струи мощностьюQ=9 л/с, бьющей вертикально вверх на высоту Н=15 м при диаметре входного сеченияD=60 мм и длине брандспойтаh=0,5 м.
Решение:
Составим уравнение Бернулли для сечений
1-1 и 3-3

относительно плоскости сравнения
(см.рис.):
![]()
![]() ,
,
где Z1=0;p1=![]() ;Z3=(H+h);p3=pатм;V3=0;V1=
;Z3=(H+h);p3=pатм;V3=0;V1=![]() .
.
Тогда
![]() .
.
Откуда найдем давление на входе в брандспойт:
 Па=1,498
Па=1,498![]() Па.
Па.
Составим уравнение Бернулли для сечений
2-2 и 3-3 относительно плоскости сравнения
![]() (см.рис.):
(см.рис.):
![]() ,
,
где Z2=0;p2=pатм; р3=ратм;Z3=H;V3=0.
Тогда получаем уравнение:
![]() ,
откуда определим скорость воды на
входеV
,
откуда определим скорость воды на
входеV![]() м|c.
м|c.
Из уравнения постоянства расхода Q=![]() найдем диаметрd:
найдем диаметрd:
d=![]() м=25,8 мм.
м=25,8 мм.
Ответ: р![]() Па;d=25,8 мм.
Па;d=25,8 мм.
3.8. Поршень в цилиндре А, двигаясь
вверх, поднимает воду из резервуара В
при разности уровней воды в цилиндре
под поршнем и в резервуаре Н=3 м. Определить
скорость движения поршня, при котором
абсолютное давление под ним р=0,65 кг/см![]() .
.
Решение:
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0 (см.рис.):
Z![]()
![]() ,
,
где Z![]() ;p
;p![]() =p
=p![]() ;V
;V![]() ;Z
;Z![]() =H;p
=H;p![]() =p
=p![]() ;V
;V![]() =V
=V![]() .
.

Тогда
![]() =H+
=H+![]() .
.
Откуда найдем скорость поршня:
V![]() =
=![]() м/с.
м/с.
Ответ: Vn=3,13
м/с.![]()
3.9. Давление в трубопроводе диаметром d=35 мм при закрытом кране равно p=3,2 кгс/см2. Определить давление перед краном при расходе воды в трубопроводе Q=7,3 л/с.
Решение:
Найдём скорость движения воды в трубе после открытия крана:
![]() м/с.
м/с.
Таким образом, часть давления (первоначального) перейдёт в скоростной напор:
Hv=![]() м.
м.
Найдём это конечное давление перед краном:
р1
=
![]()
Па = 2,88 кгс/см2.
Ответ:р1=2,88 кгс/см2.
3.10. Горизонтальный отстойник для очистки сточных вод имеет ширинуb=1,5 м и глубинуh=1,0 м. Режим движения воды в отстойнике ламинарный. Определить максимально допустимый расход сточных вод в отстойнике, еслиt в=20oC,Rе<Rе кр
Решение: Так как режим движения воды в отстойнике ламинарный, то число Рейнольда длжно быть меньше критического, которое для открытых русел может быть найдено по зависимости:
Rе’кр=![]() = 800 ÷ 900,
= 800 ÷ 900,
где R=![]() - гидравлический радиус;
- гидравлический радиус;
ω=bh–площадь гидравлического сечения отстойника;
χ= 2h+b– смоченный периметр отстойника.
Тогда R=
![]() =
=
![]() =
=![]() .
.
Найдём максимальное значение скорости,
соответствующее максимальному режиму
движения. При этом
![]() =
1.01·10-6 м2/c
(Приложение 2, стр 226 (1)).
=
1.01·10-6 м2/c
(Приложение 2, стр 226 (1)).
![]()
Замечание : скорость получилась вполне удовлетворительная для горизонтальных отстойников. Теперь найдём максимально допустимый расход сточных вод:
![]() л/c
л/c
Ответ:
![]() .
.
3.11. Под действием разности уровнейH= 2,6 м и избыточном давленииp0 = 0.3 ат по трубе нормального сечения вода перетекает из из верхнего резервуара в нижний(d1=150мм,d2=125 мм,d 3=100 мм). Определить расход воды и построить пьезометрическую линию без учёта потерь на трение.
Р ешение:
ешение:
Составим уравнение Бернулли для сечений 1-1
и 2-2 относительно плоскости сравнения 0-0
( см. рис.):
![]() ,
,
где Z1=H;Z2= 0;p1 = po +pат;p2 =pат;
V1 =V2≈ 0.
Так как по условию задачи потери на трение
не учитываются, то остаются только
потери напора на местных сопротивлениях:
hw=hl +hм= 0 +hм,
где hм =hвх +hвн.с.1 +hвн.c.2 +hвых.
В результате получаем:
![]()
или
![]() (*).
(*).
Распишем местные сопротивления:
![]() ;
;![]() :
:
![]() ;
;![]() ;
;
где
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() .
.
Подставив исходные данные в эти формулы, в результате получим:
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Потери напора в местных сопротивлениях приведем к одной скорости, в частности, к V3 :
 ;
; ;
;
![]() ;
;![]() ;
;
Представив эти значения в уравнение (*) , в результате получим:
![]() .
.
Найдём напор; соответствующий давлению
![]()
![]() .
.
Получаем уравнение:
![]() ,
,
откуда найдём скорость
![]() .
.
Найдём величину расхода воды, протекающей по трубе:
![]()
Для построения пьезометрической линии найдём величину скоростного напора в каждой из трёх труб:
 ;
;
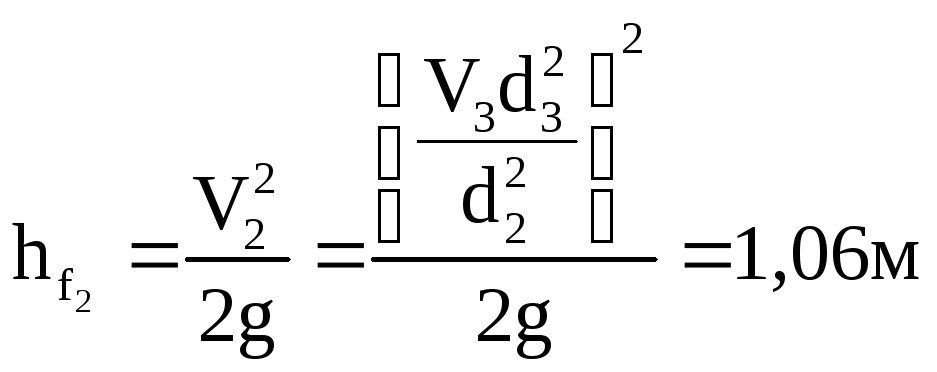 ;
;
![]() .
.
Найдём теперь потери напора на местных сопротивлениях и от этих значений вниз отложим величины скоростных напоров, в результате получим линию пьезометрических напоров p-p:
![]() ;
;
![]() ;
;
![]()
 ;
;
![]() .
.
Замечание: если бы в решении задачи были учтены потери напора на трение по длине, то линияp-pна участкахd1, d2, d3 имела бы наклонный характер.
3.12. Из открытого резервуара вода вытекает по расширяющейся трубе с диаметрамиd1=300 мм иd2=350 мм , длиной от суженной части до нижнего сеченияH2= 2,5 м. Найти давлениеpв суженной части трубы при напореH1= 0,65 м. Потерями напора пренебречь.
Решение:
З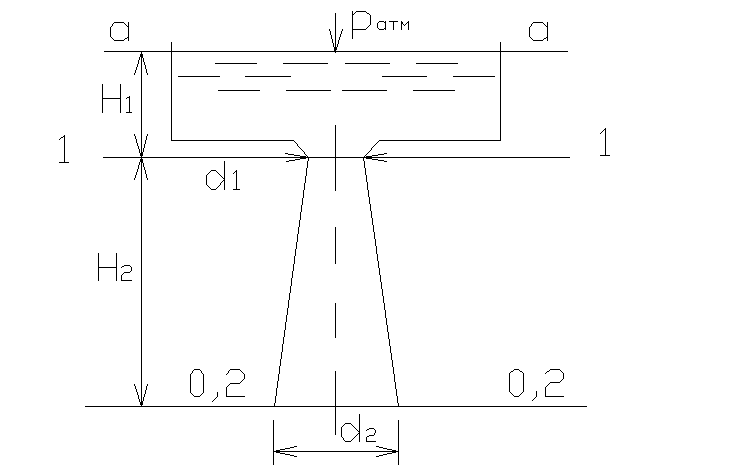 апишем
уравнение Бернулли для сечений а-а и
2-2 относительно плоскости сравнения
0-0 (см. рис.):
апишем
уравнение Бернулли для сечений а-а и
2-2 относительно плоскости сравнения
0-0 (см. рис.):
![]()
 Тогда
Тогда
![]()
откуда найдем скорость истечения
![]() :
:
![]() .
.
По уравнению постоянства расхода найдем скорость воды в сечении 1-1:
![]()
 .
.
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0:
![]()
где
![]() .
.
Тогда
![]() откуда найдём давление
откуда найдём давление

Ответ:![]()
3.13. Определить среднюю скорость движения воды в трубе, если разность показаний между динамической и статической трубками, определяемая по ртутному дифференциальному пьезометру, составляетh=20 мм.
Р ешеиие:
ешеиие:
Составим уравнение равновесия для
ртутного пьезометра:
![]() ,
,
где
![]() -
давление в точке А.
-
давление в точке А.
Получаем
![]() =h(
=h(![]() -
1).
-
1).
Следовательно, скорость на оси трубы
равна:
![]() =
=![]() =
=
=![]() =2,22м/с
=2,22м/с
Средняя скорость в трубе при турбулентном режиме движения составит
V=(0,85![]() 0,95)
0,95)![]() =(0,85
=(0,85![]() 0,95)2,22=
(1,89
0,95)2,22=
(1,89![]() 2,11)м/с.
2,11)м/с.
Ответ. V![]() 2,0м/с.
2,0м/с.
3.14. Из резервуара по трубе, имеющей сужение, протекает вода. Определить диаметр суженной частиd, при котором образуется заданная величинаhвак=10мм, если известны напор Н=10м и диаметрD=100мм.
Д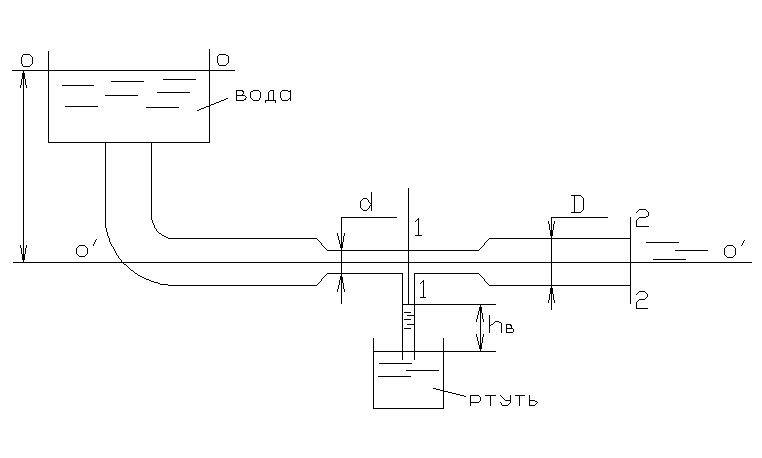 ано:
ано:
Решение:
Составим уравнение Бернулли для сечений
0-0 и 2-2 относительно плоскости сравнения
![]() -
-![]() :
:
![]()
где
![]()
![]()
![]()
![]() .
.
Тогда получаем ![]() .
.
Найдём скорость на выходе из трубы
![]() .
.
Составим уравнение Бернулли для сечений
1-1 и 2-2 относительно плоскости сравнения
![]() -
-![]() :
:
![]()
где
![]()
![]()
![]() .
.
Подставим и получим
![]() ,
,
Откуда найдём вакуум![]() .
.
Поделим на удельный вес ртути и найдём вакуумметрическую высоту
![]() ;
;
![]() или
или
![]() .
.
Найдём скорость в сечении 1-1

По уравнению неразрывности найдём диаметр в сечении 1-1
![]()
![]()
![]()
Ответ:
![]() .
.
