2.3. Сила гидростатического давления на криволинейную поверхность

Силу гидростатического давления на криволинейную поверхность определяют по формуле

где — составляющие силы избыточного давления по соответствующим координатным осям. В случае цилиндрической криволинейной поверхности

где и — горизонтальная и вертикальная составляющие силыР.

Горизонтальная составляющая избыточного давления Р_х равна си­ле давления на вертикальную проекцию криволинейной поверхности

где р_м — манометрическое давление на поверхности жидкости,

h_ц — глубина погружения центра тяжести вертикальной проекции криволинейной поверхности;

— площадь вертикальной проекции криволинейной поверхности. Если манометрическое давление на свободной поверхности жид­кости равно нулю (р_o= р_а), то

В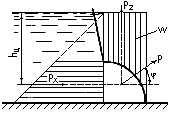ертикальная составляющая равна весу жидкости в объеме тела давления. Тело давления располо­жено между вертикальными плос­костями, проходящими через край­ние образующие цилиндрической по­верхности, самой цилиндрической поверхностью и свободной поверх­ностью жидкости или ее продолже­нием.

Если давление на свободной поверхности жидкости , то тело давления ограничивается сверху пьезометрической плоскостью, удаленной от свободной поверхности жидкости на расстояние

Направление силы Р определяется тангенсом угла:

Если криволинейная поверхность не цилиндрическая, то горизон­тальную составляющую Р_y определяют аналогично силеР_х.

Примеры

2.28. Определить силу давления воды на деталь, имеющую форму четверти кругового цилиндра радиуса =0,5 м. Найти угол, под котором эта сила направлена к горизонту. Расчет вести на единицу ширины конструкции. Высота конструкции Н=5 м.

Р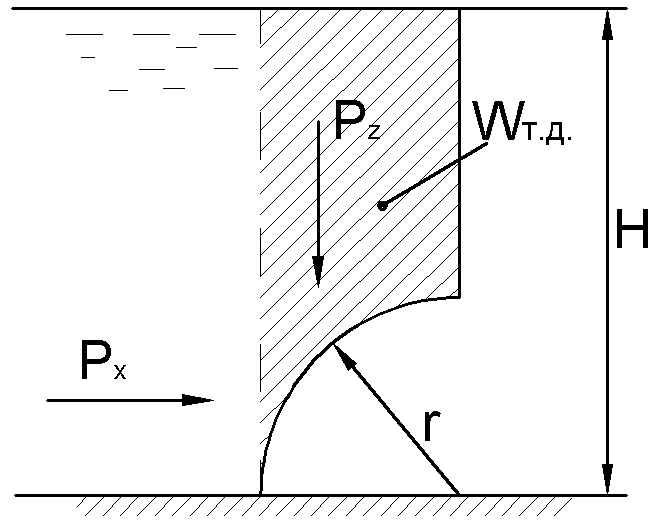ешение:

Найдем горизонтальную составляющую силы гидростатического давления воды:

Р_x=,

где h_c=H-; ;

= ^Н.

Найдем вертикальную составляющую:

P_z=.

Для чего определим объем тела давления:

^Wт.д=м3.

^{Тогда Pz =H.}

Результирующая сила найденных составляющих равна:

^{Р =3,31Н.}

Угол между линией действия этой силы и линией горизонта равен:

Ответ:P= 3, 31 H; .

2.29. Определить величину Р и направление угол α равнодействующей силы давления на цилиндрический затвор плотины, перекрывающий прямоугольное отверстиеh=D= 1,0 м и ширинойb= 5,0 м. Глубина воды слева -H₁= 3,4 м, справа -H₂=D/2.

Решение: 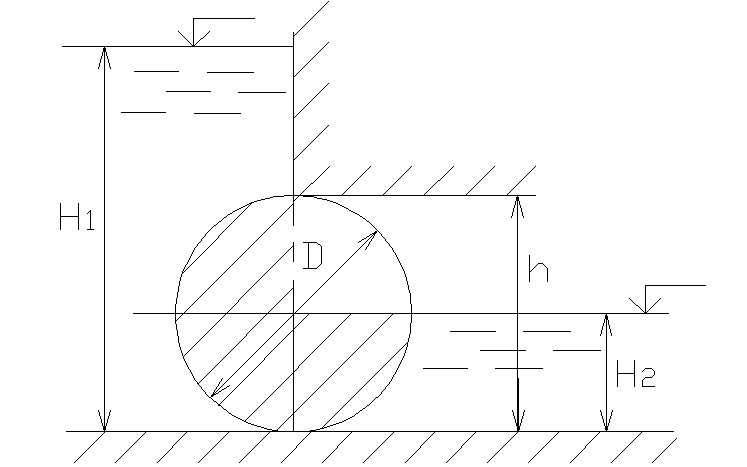Для нахождения силы гидростатического давления на цилиндр необходимо использовать зависимость:

,

^{где – горизонтальная составляющая} полной силы гидростатического давления воды;

^{– вертикальная составляющая}полной силы гидростатического давления воды.

Направление равнодействующей силы гидростатического давления воды найдем по формуле:

Горизонтальная составляющая силы давления воды:

- слева

- справа

Их равнодействующая величина равна алгебраической сумме:

.

Вертикальная составляющая силы давления на затвор равна весу воды в объеме тела давления (на рисунке заштриховано):

.

Результирующая сила гидростатического давления на цилиндрический затвор составит:

.

Направление этой силы, т.е. угол наклона к горизонту составит:

.

^Ответ:

2.30.Определить силу суммарного давления на торцовую плоскую стенку цилиндрической цистерны диаметроми точку её приложения. Высота горловины. Цистерна заполнена бензином до верха горловины.

Решение. Сила суммарного давления бензина на торцовую стенку цистерны равна

где - плотность бензина (табл. П-3).

Точка приложения (центр давления) силы суммарного давления расположена на глубине (от верхней кромки горловины)

Ответ:

2.31.Определить силу суммарного давления на секторный затвор и её направление. Глубина воды перед затвором Н=4м, длина затвораL=8м, угол.

Решение.Горизонтальная составляющая полной силы давления на секторный затвор равна силе давления на вертикальную проекцию затвора:

.

Вертикальную составляющую полной силы давления на секторный затвор определяем по формуле:

,

где W- объём тела давленияabcдлинойL;

- площадь фигурыabc;

Найдем элементы и площадь фигурыabc:

;

;

;

;

;

;

;

.

Равнодействующую сил давлений определяем по формуле:

.

Направление этой силы определяется углом :

;.

Ответ: ;.

2.32.По стальному трубопроводу диаметромподаётся вода под давлениемОпределить напряжение в стенке трубы, если ее толщина.

Решение.Суммарная сила давления, разрывающая трубу в продольном направлении, равна гидростатическому давлению, умноженному на площадь вертикальной проекции криволинейной стенки:

Разрыв происходит по двум продольным сечениям стенки трубы. Напряжение, возникающее в материале стенки, равно

Ответ: МПа

2.33.Определить силы, разрывающие горизонтальную, наполненную бензином цистерну длинойпо сечениями, если диаметр цистерны, а высота горловины. Цистерна заполнена бензином плотностью=740кг/до верха горловины.

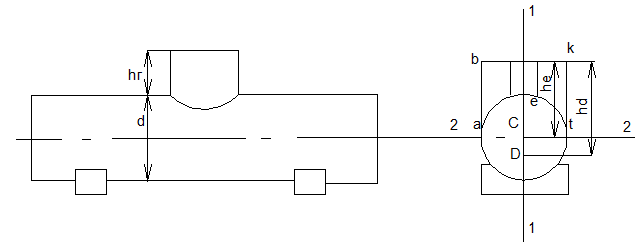
Решение.Сила, разрывающая цистерну по сечению, равна горизонтальной составляющей силы давления воды на криволинейную стенкуили:

.

Силы, растягивающие цистерну по сечению 2-2, равны силам, действующим на криволинейные стенки aetиaft. Эти силы также направлены противоположно друг другу. Сила давления на криволинейную стенкуaet

,

где W– объём телаabkt;

ω – площадь фигуры abktea;

.

Подставляя цифровые значения, находим:

.

Ответ: ;.

2.34. Для выпуска сточных вод в море построен трубопровод диаметром, уложенный по дну на глубине. Определить силы, действующие на трубопровод, когда он не заполнен.

Решение. Сила, действующая на трубопровод сверху, определяется как вертикальная составляющая суммарных сил давления на криволинейную поверхность. Она равна весу воды в объёме тела, т.е. (надлины трубопровода)

где - плотность морской воды (табл. П-3).

Сила , действующая на трубопровод снизу, больше силына величину веса воды в рассматриваемом участке трубопровода, т.е.; собственный вес трубыдолжен быть равендля того, чтобы исключить возможность её всплывания.

Силы, действующие на трубопровод по горизонтали, равны и направлены противоположно друг другу .Каждая из этих сил равна горизонтальной составляющей сил давления воды на криволинейную стенку, которая, в свою очередь, равна силе суммарного давления воды на вертикальную проекцию трубы, т.е. (на длины трубопровода)

Ответ: .

2.35.Определить силу гидростатического давления воды на ширины нижней криволинейной части сооружения, если

Решение.

1) Горизонтальная составляющая силы давления воды на криво­линейную часть сооружения равна силе давления на вертикальную проекцию этой поверхности

2) Вертикальная составляющая равна весу жидкости в объеме тела давле­ния. Обозначим площадь фигуры через. Тогда:

3) Суммарная сила давления воды на криволинейную часть сооружения

4) Расстояние от свободной поверхности воды до линии действия горизонталь­ной составляющей Р_х.

5) Вертикальная составляющая проходит через центр тяжести фигуры. Расстояниецентра тяжести фигурыот линии равно стати­ческому моменту этой фигурыотносительно линии, деленному на площадь фигуры, причем расстояние центра тяжести четверти круга от линии:

;

Сила проходит через точку пересеченияc линий действия горизонтальной и вертикальной составляющих под угломк горизонту, причем

Заметим, что при круговой цилиндрической поверхности сила всегда проходит через центр круга.

Ответ:

2.36.Определить величину и направление силы гидростатического давления воды на ширины вальцового затвора диаметром.

Решение.

1) Горизонтальная составляющая

2) Вертикальная составляющая

3) Суммарная сила давления

4) Составляющая Р_х проходит на расстоянии у_дот свободной поверхности:

составляющая проходит на расстоянииот линии, равном

5) Равнодействующая Р приложена в точкеО под угломк горизонту и про­ходит через центр круга, причем

Ответ: ;.

2.37. Определить силу гидростатического давления воды на 1м ширины вальцового затвора диаметромприи.

Решение.1) Горизонтальная составляющая силы давления воды слева

справа

2) Вертикальная составляющая силы давления воды, равная весу жидкости в объеме тела давления (на рисунке заштриховано):

где - площадь фигуры, для определения которой рассмотрим треуголь­ник:

,

3) Суммарная сила давления

4) Угол наклона силы Рк горизонту определяется по тангенсу угла :

Ответ:

2.38. Определить силу давления воды на ширины затвора, перекрывающего канал между двумя смежными камерами, если глубина воды в левой камерев правой

Решение. 1) Горизонтальная составляющая силы давления воды на затвор слева

справа

откуда

2) Вертикальная составляющая P_z равна весу жидкости в объеме тела давления (на рисунке заштриховано):

где d – длина основания тела давления;

b= 1м– его ширина. Для определениярассмотрим треугольникиАВОиАВС:

Угол

3) Суммарная сила давления на затвор

Сила Рпроходит через шарнирОпод угломк горизонту, причем

Ответ:

2.39.Цилиндр радиусоми длинойперекры­вает отверстие в дне резервуара размерамисм. Определить: силу давления воды на цилиндр при.

Решение.1) Горизонтальная составляющая силы давления воды на ци­линдр равна нулю, так как и на его основания и на продольные вертикальные проекции действуют соответственно равные и противоположно направленные силы.

2) Вертикальная составляющая равна весу жидкости в объёме тела давления (на рисунке заштриховано):

Из рисунка видно, что

.

Тогда площади сегментов s₁ иs₂определяются по формулам

Ответ:

2.40. На горизонтальной плите установлен стальной сосуд без дна в форме усеченного конуса с толщиной стенкимм. Определить при каком уровне воды в сосудеhон оторвется от плиты, если известныD=2 м,d=0,5 м, Н=2 м.

Решение: Сосуд может оторваться от плиты в том случае, если вертикальная сила гидростатического давления воды на

наклонные (конические) стенки сосуда превысит силу веса самого сосуда. Составим уравнение равновесия этих сил:

G=_т.д.;

Где G=,

т/м³=8,5Н/м³;

S_бок=- боковая поверхность конуса;

l-длина образующей:

^l=м,

тогда S_бок=м².

^{Вес сосуда равен G=8,4Н.}

Тело давления –это заштрихованная фигура, которая создает вертикальную отрывающую силу F_z.

Запишем объем тела давления:

^{Wт.д.=, ()}

где r₁–является неизвестной величиной. Выразим ее через глубину воды в сосудеh.

Для этого cоставим пропорцию для подобных треугольников АВС и АМN:

АМ=х.

^{Тогда, откуда х =}.

^{Тогда d1=2r1=D-}.

Теперь выразим радиус r₁:

^r1=.

Подставим значение r₁в уравнение ():

^Wт.д.=,

Раскрываем скобки, приведем подобные элементы, получим:

=1,04h-0,4h²-0,15h³.

^{Учитывая, что}м³,

Окончательно получаем:

0,15h³-0,4h²+1,04h-0,5=0

Способом подстановок “h” в это уравнение найдем значение:

h=0,58 м.

^{Проверка: 0,15};

0,6333-0,6350.

Ответ: h=0,58 м.

2.41. Определить силу натяжения троса, удерживающего криволинейный затвор, представляющий собой четверть кругового цилиндра радиусаR=1 м, перекрывающего канал прямоугольного сечения ширинойb=3 м. Глубина наполнения канала водойH=2 м.

Решение:Для определения силы натяжения троса составим

уравнение моментов всех сил, действующих на затвор, относительно

точки О:

;

ТR=P_zl_p+P_xl_b.

Для чего найдем составляющие Р_хи Р_z

силы гидростатического давления на криволинейный

(цилиндрический) затвор:

Р_x==10⁴= =H.

Точка приложения этой составляющей находится на расстоянии l_bот оси шарнира 0:

L_b=l_д-(H-R),

L_д=l_c+;

l_b=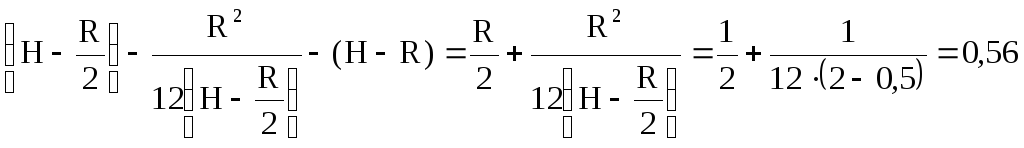м.

Составляющая P_zнаходится через объем тела давленияW_т.д.:

P_z=,

где W_т.д.=.

Тогда P_z=H.

Линия действия этой вертикальной составляющей проходит через центр тяжести фигуры 1-0-2-3-4. Расстояние l_р центра тяжести фигуры 1-0-2-3-4 от линии 0-2 равно статическому моменту этой фигурыSотносительно линии 1-0-2, поделенному на площадь фигурыF(причем расстояние центра тяжести четверти круга 1-0-4 от линии 1-0-2 равно е=0,4244R).

^м.

Тогда Т= H.

^{Ответ: Т=4,52Н.}

2.42. Найти величину и направление силы гидростатического давления воды на 1м ширины криволинейного затвора, если известны

Решение:Результирующая сила гидростатического давления равна. Найдём составляющие этой силыи:

Найдём параметры затвора:

Тогда горизонтальная составляющая равна :

Найдём вертикальную составляющую, для чего вычислим объём тела давления:,

;;;.

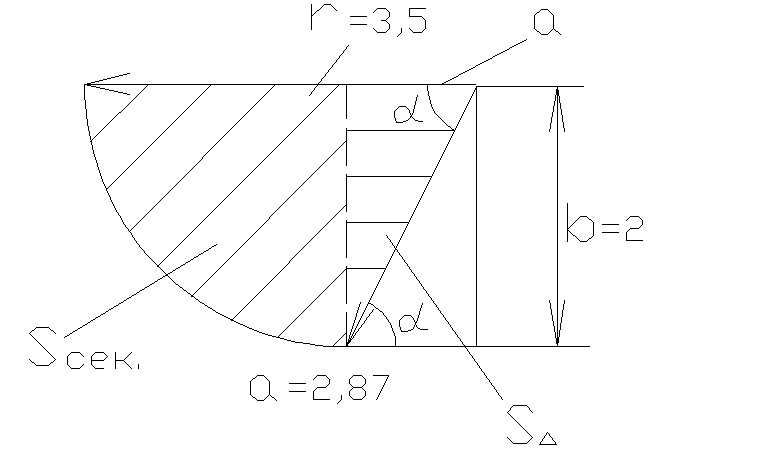Найдём площадь треугольника:

S_∆.

Площадь сектора составит:

.

Площадь тела давления:

.

Тогда объём тела давления составит:

.

.

Полная сила гидростатического давления на затвор составит:

,

а направление этой силы определяется углом φ:

.

Ответ: ,.

2.43. Определить горизонтальнуюи вертикальнуюсоставляющие силы давления воды на горизонтальный цилиндр диаметромd= 30 см, который вставлен чepeз отверстие в наклонной стенке (α = 30º) внутрь резервуара на расстоянииl= 0,8 м. Уровень воды над осью цилиндра Н = 1,0 м.

Pешение:

Горизонтальная составляющая силы давления на цилиндр определяется так:

где- заглубление центра тяжести

вертикальной проекции криволи-

нейной поверхности , т.е.

,

- площадь вертикальной проекции цилиндра:

.

Тогда:

Вертикальная составляющая силы давления воды на цилиндр равна:

гдеW– объём тела давления, который найдём из геометрии.

Рассмотрим ∆ АВС и ∆ МСD. Они равны,

так как АС = СМ = ; ВС =CD=;

Поэтому объёмы будут равны:

Тогда объём тела давления определяется так:

.

Либо объём тела давления найдём так. Из ∆ АВС:

из ∆ МСD:

Тогда:

Найдём:

.

Окончательно:

Ответ:

2.44. В прямоугольном окне вертикальной стенке установлен цилиндрический затвор (270º) диаметромD= 100 см и длинойb= 2,0 м. Определить усилие Р на цапфы и момент М от воздействия жидкости на затвор. Весом затвора пренебречь. Напор над осью крепления Н = 1,0 м.

Решение:

Так как затвор выполнен в виде цилиндра,

то для нахождения усилия на цапфы используем

расчетные формулы для определения сил

гидростатического давления на криволинейную поверхность:

где Р_х– горизонтальная составляющая силы гидростатического давления, определяется по формуле:

,

где h_C– заглубление центра тяжести вертикальной проекции криволинейной поверхности под уровень свободной поверхности (в данном случае);

− площадь вертикальной проекции криволинейной поверхности:

.

Тогда

, где

− удельный вес воды приt= 20ºС [1, табл. 1 Приложения].

P_Z– вертикальная составляющая силы гидростатического давления, которая равна весу жидкости в объеме тела давления ( тело давления показано на расчетной схеме):

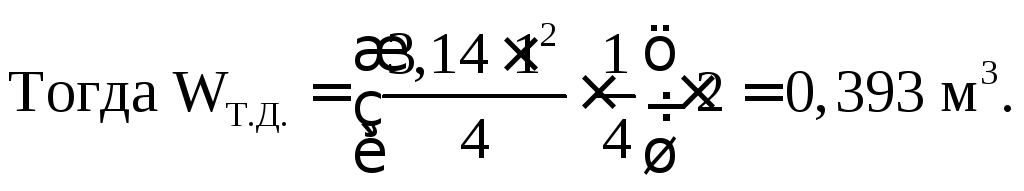
Полная сила гидростатического давления,

действующая на цапфы, расположенные на

горизонтальной оси цилиндра, равна:

.

Направление этой силы определяется тангенсом угла α:

.

Линия действия (приложения) силы Р проходит через центр цилиндра (через цапфы).

Найдем теперь момент от воздействия жидкости на затвор – М.

Этот момент в общем случае состоит из - момента от горизонтальной составляющей силы ; - момента от вертикальной составляющей силы.

Момент от горизонтальной составляющей, в свою очередь, состоит из двух моментов: - от горизонтальной составляющей, действующей на верхнюю (криволинейную поверх- ность) - от горизонтальной составляющей, действующей на нижнюю часть цилиндра.

Однако эти две горизонтальные составляющие можно привести к одной со своим плечом действия:

где

– момент инерции проекции,

Тогда

.

Таким образом, момент от горизонтальной составляющей будет:

(вращает против часовой стрелки).

Момент от вертикальной составляющей будет определяться силой и плечом.

Сила будет равна выталкивающей силе (архимедовой) численно равной весу жидкости (воды) в объеме, вытесненной 1/4 объема цилиндра:

.

Составляющая проходит на расстоянииот линииab(см. расчетную схему).

Тогда момент от равен:

(вращает по часовой стрелки).

Суммарный момент от воздействия жидкости на затвор составит:

(вращает против часовой стрелки).

Ответ: .

2.45. В шарообразном углублении радиусаналита вода весом. В воду погружен шарик радиусом. Каким должен быть вес шарика, чтобы он плавал в положении, концентричном углублению?

Решение:

Составим равенство объемов:

,

где – объем воды в углублении;

– объем погруженной части

шарика в воду;

– суммарный объем воды и погруженной части шарика.

Тогда или.

Из рисунка следует, что или.

Обозначим . Тогда уравнение примет вид:

или

, где.

Тогда .

Вычислим значения:

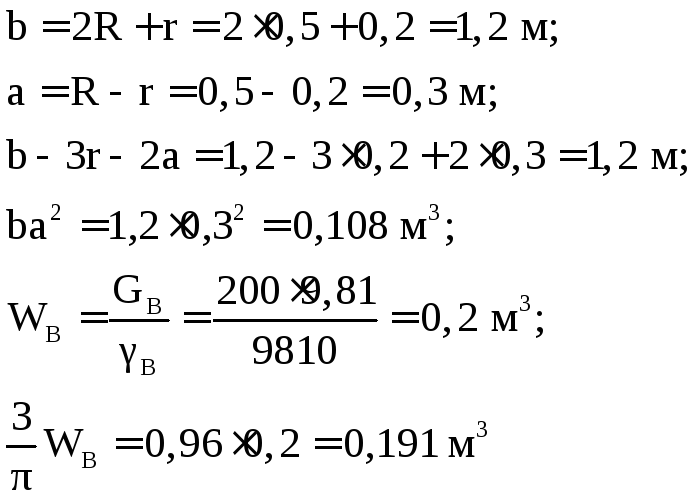
подставим в предыдущее уравнение и запишем его относительно h:

Решение этого квадратного уравнения будет h= 0,109 м.

Так как , то вес шарикаили

.

Ответ:

2.46. Определить величину и направление равнодействующей силы давления воды на цилиндрический затвор плотины, перекрывающий донное отверстие высотойh=D=1,2 м. и ширинойb= 6 м. Глубина воды слева Н₁= 3,8 м, справа Н₂=D/2.

Решение:Равнодействующая сила давления воды на цилиндрический затвор определяется так:

,

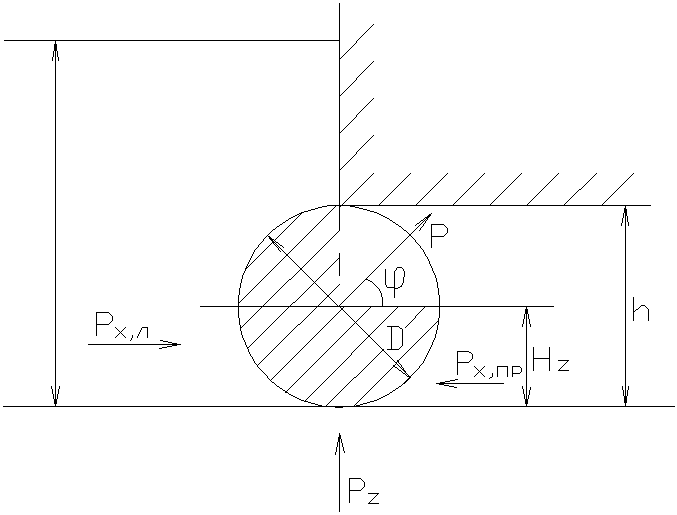
где P_Xгоризонтальная составляющая силы давления воды;

P_Z– вертикальная составляющая силы давления воды.

Найдем горизонтальную составляющую P_X. Она складывается из силы давления воды, действующей слеваP_Xли справаP_Xпр:

P_Xл= р_С.лω_{z л} = γ(Н₁ +)Db.

Аналогично:

P_Xпр= р_с.пр ω_{z пр} = γb.

Тогда равнодействующая горизонтальных сил составит:

P_X =P_Xл-P_Xпр = γ(Н₁ +)Db– γb= γb[(H₁ −)D−];

P_X = 998 ∙ 9,81 ∙ 6 ∙ [(3,8 −) ∙ 1,2 −] = 215 кН.

Найдем вертикальную составляющую P_Z. Она равна весу жидкости в объеме тела давления ( на рисунке заштриховано):

P_Z = γW= γb=γb(3/16)πD²;

P_Z = 998 ∙ 9,81 ∙ 6 ∙ (3/16) ∙ 3,14 ∙ 1,2²= 49,8 кН.

Суммарная сила давления:

.

Угол наклона силы Pк горизонту:

γ=arctg=arctg =13º5'.

Ответ: P= 220,7 кН ; γ = 13º5'.

2.47. Стальной шарик радиусомR= 7 см закрывает отверстие диаметромD= 10 см в плоской стенке, удерживаясь силой гидростатического давления. Определить, при каком напоре водыhшарик оторвется от отверстия.

Решение:

Н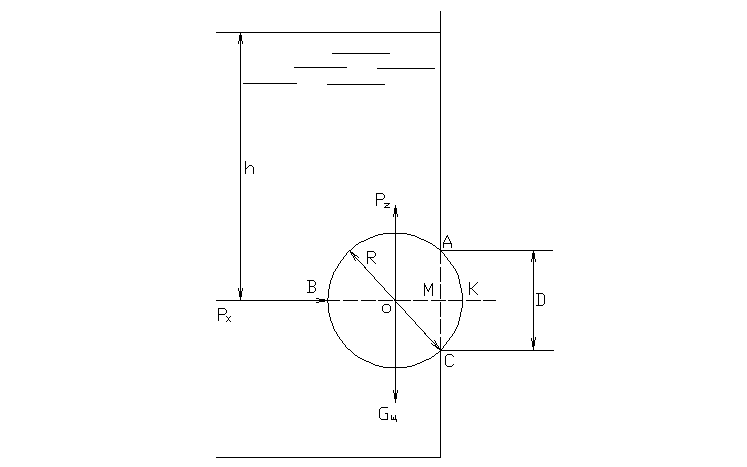айдём вес шарика:Вертикальная составляющая силы гидростатического давления воды на шарик:

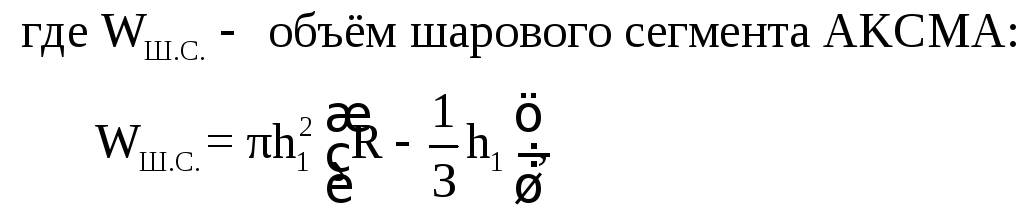
Вес шарика в воде будет на величину меньше, т.е.

Для сохранения равновесия необходимо составить уравнение моментов сил относительно точки C:

,

Тогда

откуда найдём

Ответ:

2.48. Определить величину и направление действия силы на сегментный затвор ширинойb3,0м, радиусомR2,0м, если известны углы,,.

Решение:

Сила давления жидкости на сегментный затвор равна:

,

а её направление определяется углом :

,

где ;

,

где - объём тела давления, равный величине

Найдём эти величины из геометрии:

;;

;

;

;

=;

;;

;

;

;

,;

;

;

Тогда объём тела давления равняется

.

Найдём составляющие полной силы гидростатического давления. Горизонтальная, действующая слева, горизонтальная, действующая справа

H;

H.

Их сумма равна H.

Вертикальна составляющаяH.

Полная сила гидростатического давления на затвор составит

H=54,6кН.

tgоткуда.

Ответ:Р=54,6кН;.