2.2. Сила гидростатического давления на плоскую поверхность

Сила гидростатического давления на плоскую поверхность

где h_ц— глубина погружения центра тяжести смоченной части пло­щади поверхности;

- площадь смоченной части по­верхности.

Сила избыточного гидростатического давления при р₀= р_а

Эта силаприложена в центре давления, координата которой определяется по формуле

где — координата центра тяжести смо­ченной части поверхности;

— момент инерции площади смоченной части поверхности отно­сительно горизонтальной оси, проходящей через центр ее тяжести.

Внешнее давление р₀распределено равномерно по всей площади смоченной части поверхности, поэтому его равнодействующая

приложена в центре тяжести этой поверхности.

Зная силы Р₀иР₁ и координаты точек их приложенияy_циy_д, по правилу сложения параллельных сил нетрудно определить равнодей­ствующую этих сил и точку ее приложения

Р = Р₀ + Р₁.

Сила гидростатического давления на плоскую поверхность может быть определена и с помощью эпюры давления, которая представляет собой график изменения давления в зависимости от глубины. Эпюру гидроста­тического давления строят по формуле гидростатического давления в точке. Объем эпюры равен силе гидростатического давления на плоскую поверхность. Сила проходит через центр тяжес­ти эпюры, положение которого для трапецеидальной эпюры давления на прямоугольную стенку может быть определено графически или по формулам:

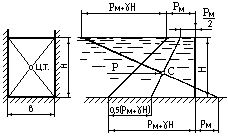
При треугольной эпюре давления на прямоугольную стенку сила проходит на расстоянии 2/З H от вершины эпюры.

Примеры

2.16Две вертикальные трубы центрального отопления соединены горизонтальным участком, на котором установлена задвижка диаметромd=0,2 м. Температура воды в правой вертикальной трубе, а в левой. Найти разность сил суммарного давления на задвижку справаи слева. Высота воды в вертикальных трубах над уровнем горизонтальной трубыh=20м.

Решение.Плотность воды при температуренайдем из табл. П-4

,

а при температуре

.

Сила суммарного давления на диски задвижки справа и слева составит

.

Разность сил суммарного давления равняется

.

Ответ:

2.17.Определить силу суммарного давления воды на плоский щит, перекрывающий канал, и усилие, которое необходимо приложить для подъёма щита если ширина каналаb=1,8м, глубина воды в нёмh=2,2м, вес щитаG=15кН. Коэффициент трения щита по опорамf=0,25.

Решение.Силу суммарного давления на щит определяем по формуле:

.

Построим эпюру избыточного гидростатического давления. В точке В гидростатическое давление составит

.

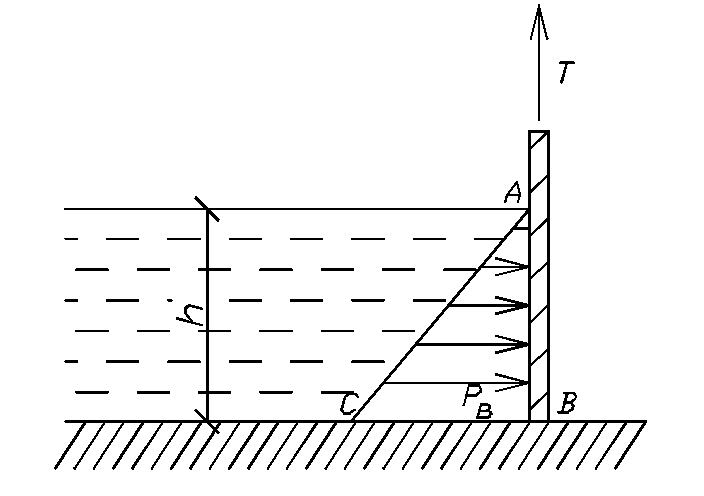
Отложим от точки В в направлении, перпендикулярном щиту, величину (со стороны действия давления) и соединим начало полученного вектора (точку С) с точкой А. Полученный треугольник АВС - это и есть эпюра гидростатического давления.

По эпюре гидростатического давления определим силу суммарного давления на щит, равную объёму этой эпюры

.

Полученная формула одинакова с ранее написанной. Подставляя в эту формулу заданные величины, находим

.

Усилие, необходимое для подъёма щита, найдем по зависимости

.

Ответ: ;.

2.18. Построить эпюру гидростатического давления на ломаную стенку резервуара и определить силы суммарных давлений и точки их приложения на участок ломаной стенки АВС шириной 1м, если;;.

Решение.Найдем избыточное гидростатическое давление :

в точке А

;

в точке В

.

Для построения эпюры гидростатического давления на стенку СВ из точки В в направлении, перпендикулярном стенке СВ, откладываем в масштабе . Полученную точку (со стороны действия давления) соединяем с точкой С. Для построения эпюры гидростатического давления на стенку АВ из точек А и В в направлениях, перпендикулярных стенке АВ, откладываем в масштабе значения давлений. Полученные точки соединяем между собой.

Абсолютные давления в точках С, В и А равны

в точке С

;

в точке В

;

в точке А

.

Эпюры абсолютных давлений построены путём увеличения давления в каждой точке на ( в принятом масштабе ).

Сила суммарного давления на стенку АВ составит

,

а глубина погружения точки её приложения (центр давления) равняется

.

Сила суммарного давления на стенку ВС

,

а глубина погружения точки её приложения

.

Ответ: ;;;.

2.19.Щит, перекрывающий канал, расположен под угломк горизонту и закреплён шарнирно к опоре над водой. Определить усилие, которое необходимо приложить к тросу для открывания щита, если ширина щитаb=2м, глубина воды перед щитом, а после щита. Шарнир расположен над высоким уровнем воды на расстоянии.Весом щита и трением в шарнире можно пренебречь.

Решение.Сила суммарного давления воды на щит составляет

слева

;

справа

.

Расстояния от шарнира до центров приложения найденных сил давления соответственно равны

,

.

Составим уравнение моментов сил относительно шарнира О:

.

Так как ,то.

Следовательно, величина усилия Т составит

.

Ответ: .

2.20. Определить величину²и точку приложения силы гидростати­ческого давления воды на вертикальный щит ширинойb = 2м, если глубина воды перед щитомH= 2,7м.

Решение.Сила давления воды на щит

Расстояние точки приложения этой силы от свободной поверхности воды

Ответ: .

2.21.На какой глубине должна находиться опора щита, чтобы при он открывался автоматически, если; угол. Указание: весом щита пренебречь.

Решение. Опора щита должна находиться в точке приложения равно­действующей силы давления воды на щит. Расчет производим на 1 м ширины щита. Предварительно вычисляем

Равнодействующая сил давления воды на 1 м ширины щита представляет собой объем эпюры давления (на рисунке за­штрихован) .

Для упрощения вычислений разде­лим эпюру на две части треугольную и прямоугольную. Объем треугольной части эпюры

Объем прямоугольной части эпюры

Равнодействующая сил давления

Координату центра давления у_д найдем из условия, что момент равнодействующейР относительно точкиА равен сумме моментов составляющих относи­тельно той же точки:

Отсюда

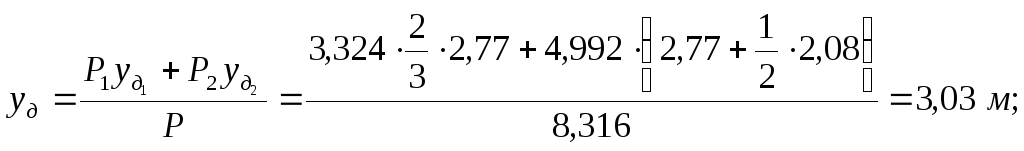
Эта задача может быть решена графически. Для этого графически находят положение центра тяжести С равнодействующей Р эпюры давления, которая про­ходит через центр тяжести эпюры С перпендикулярно к плоскости щита. На рисунке это построение выполнено дополнительными линиями.

Ответ:

2.22.Вертикальный щит, перегораживающий прямоугольный канал ширинойизготовлен из пяти досок шириной .Определить толщину доски, считая допускаемое напряжение для дерева. Глубина воды в канале.

Решение.Будем рассматривать наиболее нагруженную нижнюю доску. При­нимаем давление на каждую единицу площади нижней доски одинаковым:. Нижняя доска работает как балка на двух опорах пролетомb = 0,8м, на кото­рую действует равномерно распределенная нагрузка, где– ширина доски. Тогда:

.

Изгибающий момент посредине пролета

Толщину доски определяем из условия прочности ее на изгиб

где - момент сопротивления;

t- толщина доски;

Ответ:

2.23.Определить силу давления воды на дно сосуда и на каждую из четырех опор.

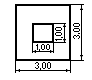
Решение.1) Избыточное давление воды в точкеА

2) Так как все точки дна находятся на одной глубине, то давление в них одинаково, а сила давления воды на дно

Эта сила является внутренней.

3) На опоры действует внешняя сила – сила тяжести воды

где W– объем воды в сосуде.

Тогда

На каждую из четырех опор передается сила

Ответ: кН;кН.

2.24.Проверить устойчивость плотин на опрокидывание при трех различных соотношениях между удельным весом кладки и удельным весом воды:

Решение.1) Расчет бу­дем вести на 1м ширины пло­тины. Подсчитаем коэффициент устойчивости для первого вари­анта плотины (а). Удерживающими силами для него являются:

- вес кладки

- вес столба воды над плотиной (треугольная призма)

Опрокидывающей силой является горизонтальная составляющая силы гидростатического давления воды

Удерживающий момент состоит из моментов сил G_в иG_котносительно воз­можной точки опрокидыванияА

Опрокидывающий момент

Коэффициент устойчивости

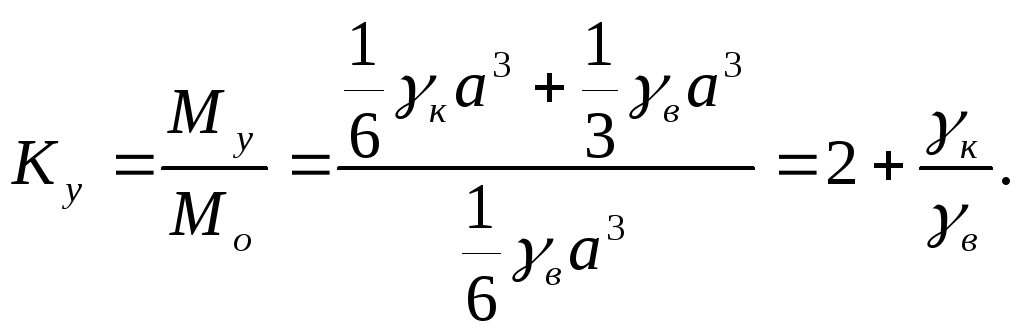
2) Для второго варианта (б) получаем:

3) Сравнивая и, видим, что более устойчивой является плотина, выполненная по первому варианту; при оба варианта равноустойчивы; при более устойчивой является плотина, выполненная по второму варианту.

2.25.Отопительный котел небольшого дома нагревает воду до температурыt₁=85⁰С. Проходя по батареям, вода охлаждается до температурыt₂=60⁰С.Определить перепад давления на вентиле, если его закрыть во время работы систем при напоре Н=3,5 м.

Решение:

Найдем давление в точках 1 и 2:

р₁= р₀-;

р₂=р₀-,

где кг/м³;кг/м³.

Разница давлений составит:

=500,95 ПаПа.

Ответ:Па.

2.26. Для увеличения жесткости стенок металлического резервуара, заполненного водой на глубину Н=2,5м, они снабжены тремя горизонтальными поясами жесткости из профильного железа. Как должны быть расположены эти пояса, чтобы каждый из них воспринимал одинаковую нагрузку. Ширина резервуара

Решение: 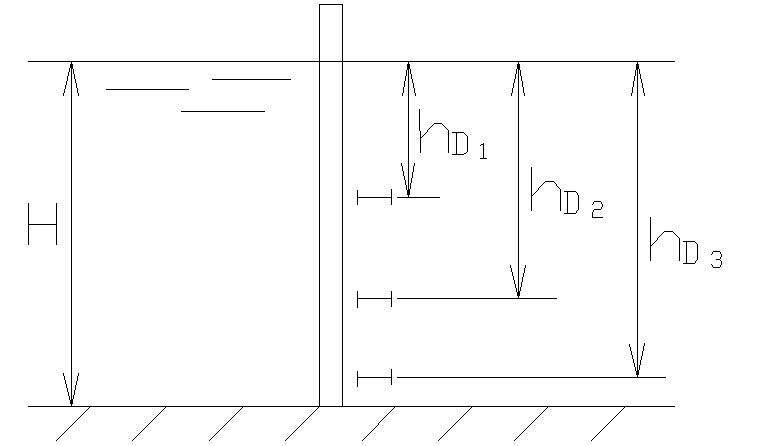Задачу решим аналитическим способом и графоаналитическим, а затем сравним результаты расчётов.

Гидростатическое давление на дне резервуара будет:

^Па.

Сила гидростатического давления воды на стенку составит:

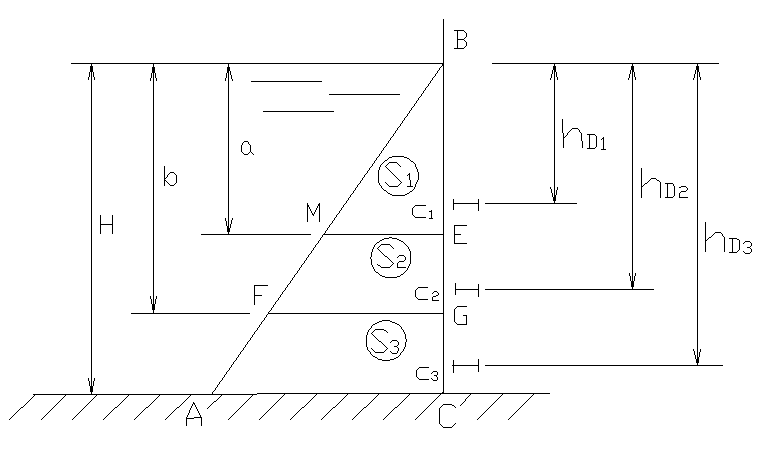
^кН.

Разбиваем эпюру АВС на три равновеликие части S₁=S₂=S₃с тем, чтобы каждый ригель воспринимал одинаковую нагрузку:

^кН.

Находим расстояние от свободной поверхности жидкости до нижней границы^{верхней эпюры}:

Аналогично находим величину :

Глубина погружения точки С₁- центра тяжести треугольникаBEM:

Заглубление точки С₂-центра тяжести трапецииEMFG- найдем как разницу величин и. Здесьn– расстояние от нижнего основания трапецииEMFGдо центра тяжести этой трапеции.

Центр тяжести трапеции определяется так:

,

где

. Тогдам.

Тогда м.

Аналогично найдем :

,

где

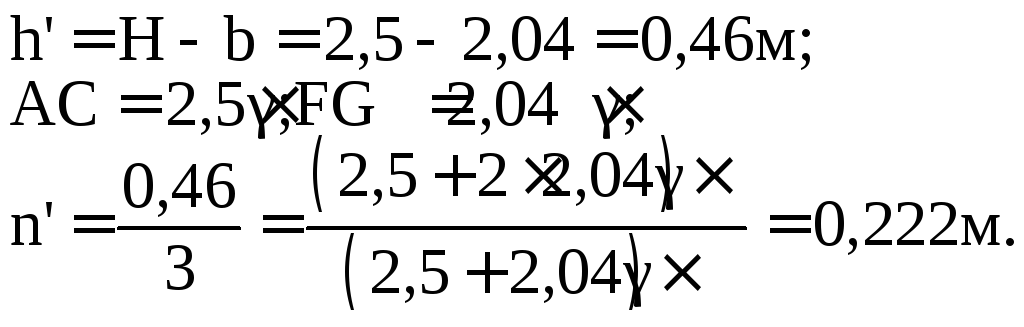
^Тогда

^{Найдем теперь величину чеpез формулы:}

^Где

^{Тогда найдём м, что совпадает с = 1.757м ( см. выше).}

^{Вычислим значение}

где

^{В результате получим:}

^{что совпадает с( см.выше).}

^{Теперь найдем значения графоаналитически ( см. рис).}

Для этого построим эпюру гидростатического давления АВС в виде прямоугольного тре-угольника с основанием АС, численно равным давлению p= 24525 Па. Затем определим силу суммарного давления при разной глубине:

при H₁ = 0.5м

P₁=p_cω=γh_cbH₁= 9.81 · 1000 · 0.5² ·1/2 = 1.226 кН;

при

при

при

при

На основании этих данных строим интегральную кривую KZ(см. рис.). ОтрезокRZделим на три части (равные). Из полученных точекaиbпроводим вертикали до пересечения с кривойKZ, тем самым поделив эпюру АВС на три равновеликие части (площади).

Глубина погружения точки C₁:

где BE= 1,44 м - определим из рис.

Положение точки С₂найдем графически. Для чего на продолженииDEотложимDM=FG, а на продолженииFG– отрезокGN=DE. Соединяем точкиMиN. Пересечение линииMNи средней линииBSдает точкуO₁, являющуюся центром тяжести трапеции, через которую проходит сила давления на площадьEG·b. Проведем перпендикуляр к плоскостиEGчерез точкуO₁и получим точкуC₂приложения силы. Аналогично находим точкуC₃. Из рисунка следует, что

BC₁= 0,97 м;BC₂=1,75 м;BC₃=2,30 м

^Ответ:

2.27. Круглое отверстие диаметромdв вертикальной стенке резервуара с водой перекрыто плоским клапаном. Найти величину и точку приложения силы, прижимающей клапан к стенке, если центр отверстия находится ниже свободной поверхности жидкости на величинуh.

Решение:

Величина силы, прижимающей крышку к стенке, определяется избыточным (манометрическим) давлением воды:

P=p_cω,

где p_c– избыточное давление в центре тяжести клапана (отверстия):

p_c=γh;

ω - площадь клапана:

ω= .

P=p_cω=γh.

P= 998 ∙ 9,81 ∙ 3,0 ∙ = 3689 Н = 3,69 кН

Точку приложения этой силы найдем по формуле:

h_D =h_c +,

где h_c=h;.

Тогда центр давления будет заглублен на величину

.

Таким образом, точка приложения силы (центр давления), прижимающей клапан к стенке, будет на 3 мм ниже центра тяжести отверстия (клапана).

Ответ: P= 3,69 кН;h_D = 3,003 м.