Примеры

4.1.Через цилиндрический насадок, расположенный в стенке, расходуется вода в количествел/с. Диаметр насадкасм, длинасм. Определить напорHнад центром насадка, скоростьи давлениев насадке (в сжатом сечении).

Решение.Длина насадка

см, следовательно, можно принять коэффициент расхода μ=0,82. Приd=3,8смплощадьсм². Напор над центром насадка найдем из формулы

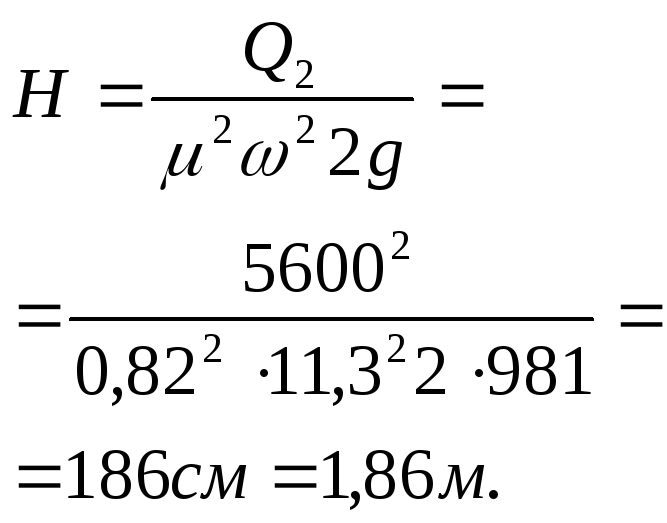
Скорость в выходном сечении насадка составит

Из условия неразрывности определим скорость в сжатом сечении, полагая,

Для определения давления составим уравнение Бернулли для двух сеченийО-ОиС-С при плоскости сравнения, проходящей через ось насадка,

Так как между сечениями будут потери только на сопротивление тонкой стенки, то . Полагая, имеем

.

Подставляя численные значения, получим высоту давления :

Давление

Недостаток до атмосферного давления в сжатом сечении

Высота вакуума, выраженная в метрах водяного столба,

Такой же результат получим, применив формулу

Ответ:

4.2. Резервуар разделен на три отсека перегородками, в которых имеются отверстия: в первой перегородке прямоугольное с площадьюсм², во второй перегородке – квадратное, примыкающее одной сторонойа=4смк дну. В наружной стенке отверстие круглоеd=3,0см. Разность между отметкой уровня воды в первом отсеке и отметкой центра наружного отверстияH= 3,10м.

Определить расход воды из резервуара и напоры ,ипри установившемся движении в двух расчетных случаях:

1. при истечении воды из наружного отверстия в атмосферу;

2. в случае если к наружному отверстию присоединен цилиндрический насадок.

Решение. 1) Согласно условию сумма напоров

,

причем любой из этих напоров , определяется формулой

.

Подставляя выражение в исходное уравнение, получим:

.

Прямоугольное и круглое отверстия полагаем находящимся в условиях полного совершенного сжатия, поэтому считаем . Для квадратного отверстия, расположенного у дна, коэффициент расхода определим по формуле

Подставляя числовые значения ,,H, определим расход по формуле

По найденному расходу вычислим напоры

;;

.

Проверка дает .

2) Если к выходному отверстию присоединим насадок, то некоторый период времени движение в отсеках будет неустановившимся. Через насадок пойдет большой расход (по сравнению с расходом через отверстие), но напор будет падать, так как для пропуска большего расхода должны увеличиться напорыи.

После того, как движение примет установившейся характер, будет применимо уравнение для расхода, из которого определим, полагая , расход

и напоры

;;.

При этом, как и в первом случае,

.

Ответ: 1)

2)

4.3. Определить расход из резервуара через два цилиндрических насадка и величину вакуума в них. Один насадок расположен горизонтально в боковой стенке резервуара на расстояниисмот дна, другой – вертикально в дне резервуара. Размеры насадков одинаковы:см,см. Глубина воды в резервуаресм.

Решение.1) Напор над центром горизонтального насадка

.

Пренебрегая скоростью подхода, так как размеры резервуара достаточно велики, примем .

Расход из горизонтального насадка

.

Вакуум в сжатом сечении горизонтального насадка

.

2) Расход через насадок, расположенный в дне резервуара, соответствует напору . Скоростью подхода, как и в первом случае, пренебрегаем

Расход из резервуара через оба насадка будет

.

Для определения вакуума в сечении составим уравнение Бернулли для сечений1-1и, взяв плоскость сравнения на уровне,

.

Отсюда, принимая потери на сопротивление тонкой стенки, получим выражение высоты вакуума

или

.

Полагая и, получим:

.

Подставляя числовые значения величин

,,,,~ 0 и принимаяа~, будем иметь:

,

или

.

Для условий задачи величина вакуума в вертикальном насадке будет

.

Ответ: ;;.

4.4. Из резервуара с площадью поперечного сечениячерез отверстие в стенке вода поступает в смежный резервуар, имеющий площадь. Отверстиерасположено на высотеот дна. Через какое времяtпосле открытия отверстия из первого резервуара во второй вытечет вода в количестве, если в момент открытия отверстия глубина в первом резервуаре была, а второй был пуст. Притока в резервуары извне нет.

Решение.Времяtбудет состоять из двух периодов:

а) истечение при переменном напоре в атмосферу за время наполнения второго резервуара до центра отверстия;

б) истечения при переменном напоре под переменный уровень.

Объем во втором резервуаре от дна до отметки центра отверстия

.

При вытекании во второй резервуар количества воды в объеме уровень воды в первом резервуаре понизиться на

.

Время уменьшения напора отдобудет найдено по формуле

.

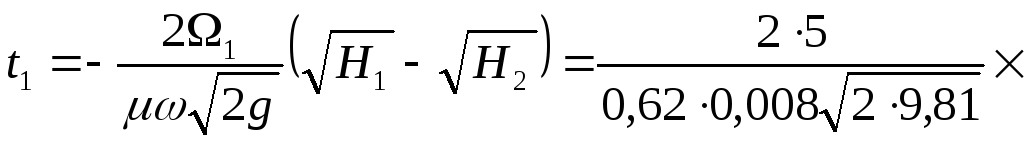
По условию во второй резервуар ещё должно поступить количество воды

.

При вытекании воды уровень в первом резервуаре понизиться на

.

Одновременно уровень воды во втором резервуаре повыситься на

.

Изменение напора будет от до.

Время на этот процесс определиться по формуле

.

Суммарное искомое время будет

.

Ответ: .

4.5. Цилиндрический бак с площадьюи высотой, заполненный до краев водой, нужно опорожнить за время.

Определить необходимую для этого площадь двух одинаковых отверстий, одно из которых расположено в центре дна, другое в стенке, на половине высоты бака.

Решение.Опорожнение верхней половины бака будет определяться дифференциальным уравнением

,

отсюда

.

Освобождаясь от иррациональностей в знаменателе и подставляя пределы при опорожнение верхней половины резервуара, получим

.

Вводя переменную , пределы которой будут отдо, перепишем уравнение:

.

В результате интегрирования получим

.

Опорожнение нижней половины бака определиться по формуле

.

По условию задачи

.

Подставляя числовые значения, получим:

,

отсюда

.

Ответ: .

4.6. Цилиндрический резервуар имеет площадь поперечного сечения. В его стенке на расстоянииот дна расположено круглое отверстиесм. Постоянный приток воды в резервуарОпределить глубину водыв резервуаре через 20минпосле открытия отверстия, если в момент его открытия глубина равнялась.

Решение.Расход через отверстие при напореибудет

. Так как начальный расходменьше притока, то напор над отверстием увеличивается. Сначала определим напор, при котором притоки расход из отверстия будут одинаковы. Из формулы найдем напор

.

Изменение напора от дов цилиндрическом резервуаре при наличии притоказа времяопределяется формулой.

или, упрощая уравнение (и полагая ), получим:

.

Из этого уравнения подбором определим . Следовательно, черезпосле открытия отверстия глубина в резервуаре будет.

Ответ: .

4.7.Щитовое отверстие имеет ширинуи высоту. Щит приподнимается равномерно со скоростью. Определить объем воды, вытекающий за времяполного открытия отверстия. Напор над центром отверстия. Истечение свободное. Коэффициент расхода отверстия.

Решение:

Объем воды, вытекающий из отверстия за время

.

Расход из отверстия

,

где и- переменные, определяемые скоростью и временем открытия,

и.

Тогда

.

Полный объем за время открытия щита

.

Для решения интеграла введем подстановку

При этом пределы переменной yбудут отHдо.

.

Решение интеграла дает

.

Подставляя числовые значения в решение, получим объем .

Ответ: .

4.8. В верхний сосуд поступает вода с расходомQ = 0,25л/с, которая затем перетекает через малое от верстие в дне диаметромd₁= 10ммв нижний сосуд, имеющий также малое отверстие в дне диаметромd₂= 15мм.

Определить:

а) напоры Н₁ иН₂в обоих сосудах;

б) при каком диаметре d₂ напорН₂будет вдвое меньше, чемН₁.

Решение:

а) Определим в обоих сосудах напоры Н ₁ и Н₂, при которых расходыQ₁ и Q₂ станут равными притоку водыQ= 0,25л/с.Расходоткуда

см =1,35 м;

см =0,27 м;

б) Находим диаметр d₂, при которомсм = 0,675 м.

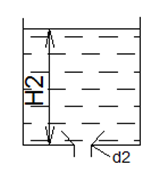
Из формулы определяем

см²

Тогда

Ответ:d=0,012 м.

4.9.Открытый понтон, имеющий форму прямо­угольного параллелепипеда с ширинойВ= 2м; длинойL= 5м; высотойН= 0,5ми весомG = 1000 кг получил в дне пробоину диа­метромd. Считая пробоину затопленным отверстием в тонкой стенке, определить время, в течение которого понтон затонет, еслиd= 15мм:

Решение.1) Определим осадку понтона до получения пробоины:

2) Найдем расход воды через пробоину при напоре h:

3) Найдем увеличение глубины воды в понтоне в результате притока за секунду

4) Определим осадку понтона от поступающей в него воды за секунду

Как видим, . Значит, напор над пробоиной остается постоянным в течение всего времени погружения понтона.

5) Понтон затонет, когда его вес станет равным или когда в него поступит объем воды, откуда время от момента получения пробоины до затопления понтона

с= 7ч30 мин.

Ответ:7ч30 мин.

4.10.Из закрытого сосуда диаметромD= 0,5м, в верхнюю крышку которого вставлена открытая трубка, вода выте­кает в атмосферу через малое отверстие в дне диаметромd= 15мм.

Определить время опорожнения сосуда при Н= 1,2миh= 0,5м.

Решение.1) При опорожнении сосуда в силу закона Бойля — Мариотта давление на его поверхности уменьшается, вследствие чего в открытой трубке уровень воды быстро понизится до положения1-1. С этого момента воздух через трубку будет прорываться в верхнюю часть сосуда. Так как во всех точках горизонтальной плоскости1-1давление одинаково, то давлениебудет оставаться постоянным и равным атмосферному давлению.

2) Исходя из этого, найдем сначала время, за которое вытечет объем воды, находящийся выше уровня 1-1

м³;

= 0,000344м³/с;

с.

3) Время, за которое вытечет оставшийся объем воды

м³,

найдем по формуле

4) Полное время опорожнения сосуда

с = 16 мин10 с.

Ответ:t =16 мин10 с.

4.11.Цилиндрическая бочка радиусомR= 0,3ми высотойh= 1мзалита водой , давление на свободной поверхности которой равно атмосферному. Определить время опорожнения бочки через отверстие диаметромd= 2смв боковой стенке при гори­зонтальном положении.

Решение.1) Составим дифференциальное уравнение опорожнения неприз­матического сосуда, для чего рассмотрим этот процесс в течение бесконечно малого отрезка времениdt, за который площадь зеркала воды в бочкеи напор z над отверстием меняются весьма незначительно. Пусть за времяdtуровень воды в боч­ке опустился на величинуdz. Тогда объем вытекшей воды за отрезок времениdt

где dz— отрицательная величина, так как изменение напораzпроисходит против положительного направления оси OZ. Кроме того, элементарный объем равен

где — площадь отверстия.

Приравнивая правые части выражений для dW, получаем дифференциальное уравнение

интегрируя которое, можем найти время опорожнения бочки.

2) Найдем площадь зеркала воды в бочке как функцию z:

3) Подставляя значение в дифференциальное уравнение и интегрируя от 2rдо 0, получаем

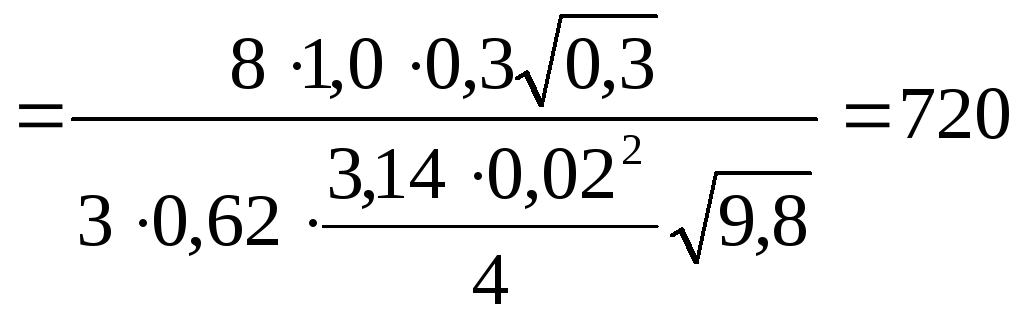с= 12мин.

Ответ:t= 720с.

4.12.Вода расходомQ= 15л/споступает в бак, разделен­ный на два отсека перегородкой толщиной 30мм, в которой про­сверлено четыре ряда отверстий диаметромd₁= 10мм, причем расстояние между центрами отверстий в ряду и между рядами отверстийа= 50мм. Из второго отсека вода вытекает через внеш­ний конический насадок диаметромd₂= 80мм. Определить глубинуH₁иH₂в обоих отсеках, если в одном ряду 48 отверстий.

Решение.1) ГлубинуН₂во втором отсеке найдем из условия, что заданный расходQ =15л/спроходит через отверстия в перегородке и через конический насадок:

откуда

2) Для определения H₁воспользуемся формулой для расхода через затопленное отверстие, в которойH= =Н₁ -H₂; считая, что приа= 50ммвсе отверстия в перегородке работают как внешние цилиндрические насадки независимо друг от друга, имеем

где n= 48 4 = 192 — количество отверстий в перегородке.

Отсюда получаем

Ответ:

1Размерность основных физических величин и их производных, применяемых в гидравлике, приведены в приложении.

2Для приобретения навыка перевода единиц измерения из СИ во внесистемные единицы, задачи решены с использованием систем единиц измерения СГС и МКГСС.

109