1.5. Функции k-значной логики

Для описания дискретных устройств наряду с булевыми функциями применяются функции, у которых аргументы и сами функции принимают значения из множества, содержащего k элементов (0,1.. k-1) [1].

Определение. Функция, принимающая значения из множества

{0,1.. k-1}, аргументы которой также принимают значения из этого множества, называется функцией k-значной логики.

Булева функция есть функция двухзначной логики. Функция

k - значной логики может быть задана таблицей истинности вида:

x1	x2	...	xn	f(x1... xn)
0	0		0	f(0,0,...,0)
0	0		1	f(0,0,...,1)
0	1		0	f(0,1,...,0)
0	1		1	f(0,1,...,1)
...	...	...	...	...
k-1	k-1		k-1	f(k-1,k-1,...k-1)

Число k - ичных наборов длины n равно kи на каждом из них значение функции может задаватьсяk способами, поэтому число функций k - значной логики определяется числом k. Аналогично двузначной логике вk - значной логике выделяются элементарные функции:

1. Квазиконъюнкция

2. Квазидизъюнкция

3. Сумма по модулю k

{x₁ x₂}_{mod k}

Значение функции равно остатку от деления суммы x₁ + x₂ на k..

4. Произведение по модулю k

{x₁x₂}_{mod k}

Значение функции равно остатку от деления произведения x₁ и x₂ на k.

5. Функция Вебба, (стрелка Пирса  ),

{max(x₁, x₂)+1}_{mod k}

6. Цикл (циклическое отрицание)

7. Функция инверсии

.

В алгебре k - значной логики действуют законы аналогичные законам булевой алгебры. Кроме того к элементарным функциям относятся следующие характеристические функции:

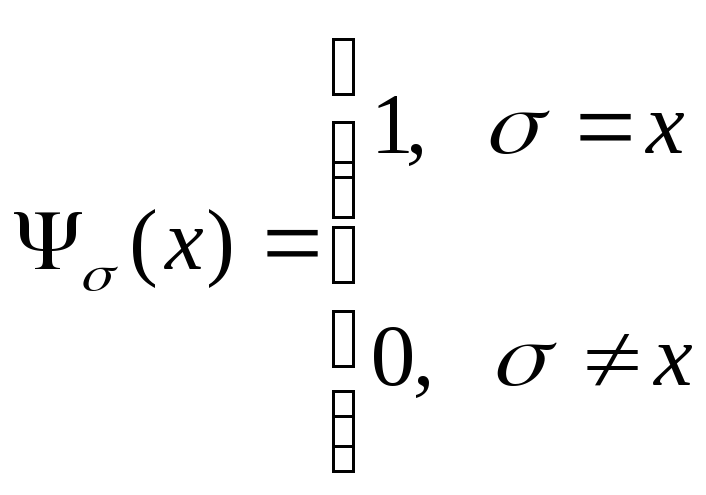= ( 0, 1, ..., k-1).

Построим таблицы, задающие введенные элементарные функции. В трехзначной логике f =0, f = 1, f = 2 будут представлять собой константы.

x1	x2			x1  x2	x1 x2	x1 x2
0	0	0	0	1	0	0
0	1	0	1	2	1	0
0	2	0	2	0	2	0
1	0	0	1	2	1	0
1	1	1	1	2	2	1
1	2	1	2	0	0	2
2	0	0	2	0	2	0
2	1	1	2	0	0	2
2	2	2	2	0	1	1

x	0	1	2
0	2	0	0	2	1
1	0	2	0	1	2
2	0	0	2	0	0

1.6. Основные понятия трехзначной логики

Трёхзначная логикабыла исторически первой многозначной логикой, и является простейшим расширением двузначной логики. Перечень истинностных значений трёхзначной логики помимо «истинно» и «ложно» включает также третье значение, которое трактуется как «неопределено», «неизвестно» или «ошибочно». В последнем случае логику обычно называютчастичной.

Важным свойством трёхзначных логик, отражающим их адекватность, является то, что все они представляют собой расширенияклассическойдвузначной логики.

В трехзначной логике имеют место следующие соотношения:

1.   x = x

2. x & x = x

3. x & 0 = 0

4. x & 2 = x

5. 

6. 

7. 

8. x  1 = x

9. x  0 = 0

10. x  0 = x

11. 

12. 

Функции квази-дизъюнкции, квази-конъюнкции и отрицания связаны между собой формулами де Моргана.

x						0	1	2
0	1	2	1	2	2	2	0	0
1	2	0	2	1	2	0	2	0
2	0	1	2	2	1	0	0	2