Тавровые и двутавровые сечения
Пример 7.
Дано: сечение размерами
=1500
мм,
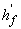=50
мм,
=200
мм,
=400
мм;
=80
мм; бетон класса В25 (
=14,5
МПа), арматура класса А400 (
=355
МПа); изгибающий момент
=260
кН·м.
Требуется определить площадь сечения продольной арматуры.
Расчет.
мм. Расчет производим согласно п.3.25 в
предположении, что сжатая арматура по
расчету не требуется.
Проверим условие (3.32),
принимая
=0:
Н·мм
=
кН·м
кН·м, т.е. граница сжатой зоны проходит
в полке, и расчет производим как для
прямоугольного сечения шириной
мм согласно п.3.21.
Вычисляем значение
(см. табл.3.2),
т.е. сжатая арматура действительно по расчету не требуется.
Площадь сечения растянутой арматуры вычисляем по формуле (3.22)
мм
.
Принимаем 4
28(
=2463
мм
).
Пример 8.
Дано: сечение размерами
=400
мм,
=120
мм,
=200
мм,
=600
мм;
=65
мм; бетон класса В15 (
=8,5
МПа); арматура класса А400 (
=355
МПа); изгибающий момент
=270
кН·м.
Требуется определить площадь сечения растянутой арматуры.
Расчет.
мм. Расчет производим согласно п.3.25 в
предположении, что сжатая арматура по
расчету не требуется.
Так как
Н·мм=
=
кН·м
=
кН·м,
граница сжатой зоны проходит
в ребре и площадь сечения растянутой
арматуры определим по формуле (3.33),
принимая площадь сечения свесов равной
мм
.
Вычисляем значение
,
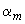при
(см. табл.3.2), следовательно, сжатая
арматура не требуется.
мм
.
Принимаем 4
25
(
=1964
мм
).
Пример 9.
Дано: сечение размерами
=400
мм,
=100
мм,
=200
мм,
=600
мм;
=70
мм, бетон класса В25 (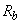
=14,5
МПа); растянутая арматура класса А400
(
=355
МПа); площадь ее сечения
=1964
мм
(4
25);
=0,0;
изгибающий момент
=300
кН·м.
Требуется проверить прочность сечения.
Расчет.
мм. Проверку прочности производим
согласно п.3.23, принимая
=0,0.
Так к.
Н
Н, граница сжатой зоны проходит в ребре,
и прочность сечения проверяем из условия
(3.28).
Для этого по формуле (3.29)
определим высоту сжатой зоны, приняв
площадь свесов равной
мм
:
мм
мм (где
найдено из табл.3.2).
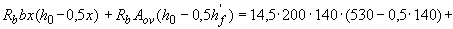
Н·мм =
кН·м
=
кН·м,
т.е. прочность сечения обеспечена.