61

5. Отображения множеств. Типы отображений. Обратное отображение. Суперпозиция отображений Содержание

§ 5. Отображения множеств. Типы отображений. Обратное отображение. Суперпозиция отображений 47

5.1. Определение отображения множеств 47

5.2. Основные типы отображений 50

5.3. Образы и прообразы множеств при отображениях 52

5.4. Понятие многозначного отображения 54

5.5. Обратное отображение 54

5.6. Суперпозиция отображений (сложная функция) 55

5.7. Упражнения для самостоятельной работы 58

Вопросы для самопроверки 60

Глоссарий 60

1. Определение отображения множеств

Наряду с понятиями множества и элемента множества в математике первичным понятием являетсяпонятие соответствия. Это понятие присутствует неявным образом при описании понятия множества: каждому из элементов поставлено в соответствие некоторое свойство, позволяющее судить о том, является ли этот элемент элементом данного множества или нет. Среди всевозможных соответствий важнейшими в математике являются функции, или отображения множеств.

Определение отображения множеств или функции

Пусть заданы непустые множества X иY. Соответствие, при котором каждому элементусоответствует единственный элемент, называетсяотображением множества X в  множество Yилифункцией, определенной на множестве X и принимающей значения в множестве Y.

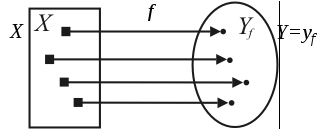
Иллюстрация к понятию отображения множества X в множествоY, то есть к понятию функции приведена на рис. 28.

Рис. 28

каждому элементу поставлен в соответствие единственный элемент.

Пример 1 (соответствия, не являющиеся функциями)

1)		не каждому элементу поставлен в соответствие элемент;
2)		одному элементу поставлены в соответствие два элемента.

Обозначения для отображения множеств, или функции

Отображение множеств, или функция обозначается одним из следующих способов:

,;		;		,,;
;		.

При этом элементназываетсянезависимой переменной, илиаргументом функции; соответствующий элементназываетсязависимой переменной. Говорят, что между элементамиx иy существуетфункциональная зависимостьf.

МножествоXназываетсямножеством задания функции f(илимножеством определения f). Множество тех элементов, каждый из которых поставлен в соответствие хотя бы одному элементу, называетсямножеством значений функцииfи обозначается:

.

Очевидно, что , то есть множество значений функции является подмножеством множестваY, в частности,может совпадать сY.

Пример 2 (отображение множеств)

1) X — множество треугольников на плоскости,

Y — множество положительных действительных чисел;

площадь треугольника S — это есть функция, определенная на множестве X и принимающая значения в множестве Y, или отображение множества X в множество Y, то есть ;

если Р – это периметр треугольника, то ; еслиM – это длина наибольшей медианы треугольника, то ;

2) функция :

;;

3) функция :

;;; ;

4) последовательность с общим членом есть функция, отображающая множество натуральных чиселв множество действительных чисел, например,:;

5) функция Дирихле: .

2. Основные типы отображений

Рассмотрим отображение .

1. Если множество значений функции совпадает с множествомY, то есть, то отображениеf называетсяотображением множества X на множество Y,илисюръекцией.

2. Если в отображенииразным элементамсоответствуют разные элементы, то есть прибудет, то отображение множестваXв множествоY называетсяинъекцией.

3. Если отображение является одновременно сюръекцией и инъекцией, то оно называетсябиекцией.

Иллюстрации к разным типам отображений приведены на рис. 29-31.

11.	Рис. 29	сюръекция
22.	Рис. 30	инъекция
33.	Рис. 31	биекция

Очевидно, что биективное отображение являетсявзаимно однозначным отображением, то есть выполняются следующие условия:

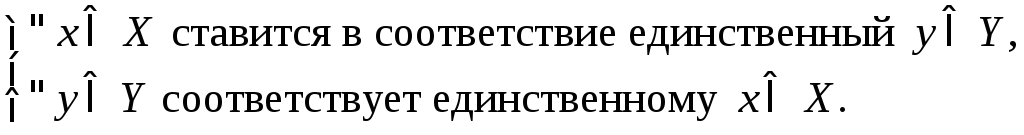
Пример 3 (отображения разных видов)

1) — биекция;

—биекция;

2)	— сюръекция, но не инъекция; — инъекция, но не сюръекция; — сюръекция и инъекция, то есть биекция;

3) функция Дирихле— сюръекция, но не инъекция, следовательно, не биекция.