Лекция 6
6.1.Численные методы решения дифференциальных уравнений
Висследовании многих процессов и явлений используются математические модели, созданные на базе дифференциальных уравнений.
Примерами таких моделей являются описания процессов динамики механических систем, процессов, описывающих движение жидкости, радиоактивный распад и т. п. явлений.
Дифференциальное уравнение — это уравнение, в котором неизвестной величиной является некоторая функция. При этом в самом уравнении участвует не только неизвестная функция, но и различные производные от неё. Таким образом, дифференциальным называется уравнение, в запись которого входят одна или несколько производных от искомой функции.
Если искомая функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, то уравнение называется обыкновенным. Так, например, уравнения
m dv |
= mg − kv, |
|
(1) |
|||
dt |
|
|
|
|
|
|
d 2 y |
= |
1 |
1 |
dy |
2 |
|
dx 2 |
a |
+ |
|
(2) |
||
|
|
dx |
|
|||
являются обыкновенными дифференциальными уравнениями. Уравнения, в которых используются функции от двух и более
независимых переменных и присутствуют частные производные по
этим переменным, называются дифференциальными |
уравнениями |
||
с частными |
производными. |
Классическим |
примером |
дифференциального уравнения с частными производными является волновое уравнение колебаний струны
∂2u |
= a2 ∂2u |
(3) |
∂t 2 |
∂x2 |
|
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение. Так уравнение (1) является уравнением первого порядка, а уравнения (2) и (3) - уравнениями второго порядка.
1
Решением дифференциального уравнения называется функция, при подстановке которой в уравнение оно преобразуется в тождество.
Так решением уравнения (1), определяющего изменение скорости падения тела в вязкой среде будет функция вида
|
|
k |
|
|
v = Ce |
− |
|
t + mg |
(4) |
m |
||||
|
|
|
k |
|
Эта функция удовлетворяет уравнению (1), при любом значении произвольной константы С. Решение (4) называется общим решением или общим интегралом уравнения (1).
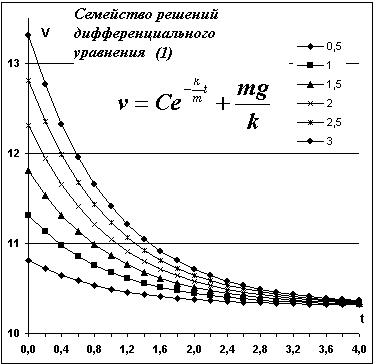
Геометрически общее решение представляет собой семейство кривых, зависящих от параметра С.
Каждое конкретное числовое значение произвольной константы С определяет частное решение уравнения.
Рис. 6.1. Семейство решений для значений константы С от 0,5 до 3
Общая форма представления обыкновенного дифференциального уравнения порядка n может быть записана в виде
F( x, y, y' , y" ,..., y( n ) ) = 0 |
(5) |
Если уравнение (5) удаётся разрешить относительно старшей производной y(n), то получаем уравнение
y( n ) = f ( x, y, y' ,..., y( n−1 ) ) |
(6) |
2
Эта форма записи дифференциальных уравнений называется нормальной. В различных исследованиях чаще всего рассматриваются уравнения и системы уравнений, записанные в нормальной форме.
В вычислительной практике, обычно, требуется найти некоторое частное решение дифференциального уравнения, соответствующее дополнительным условиям, наложенным на исследуемый процесс внешней средой.
Общее решение уравнения (6) записывается в виде
y =ϕ( x,c1 ,c2 ,...,cn ) |
(7) |
где с1, с2, ... ,сn - произвольные постоянные.
Частные решения уравнения (5) или (6) определяется при задании n дополнительных условий, позволяющих определить значения этих постоянных. В зависимости от вида этих условий различают две основные задачи:
-задача Коши и
-краевая задача.
Впостановке задачи Коши задаются начальные условия, записываемые в виде
y(x0) = y0, y'(x0) = y1, y"(x0)=y2, ... , y(n-1)(x0)=yn-1 |
(8) |
Эти условия определяют значения функции y(x) и её производных
водной начальной точке х0.
Впостановке краевой задачи определяются значения искомой функции в нескольких точках области интегрирования. Эти условия называются граничными. Более подробно особенности постановки краевой задачи рассмотрим позднее.
Впостановках задач Коши независимой переменной чаще всего является время, а в постановках краевых задач независимыми переменными обычно являются некоторые геометрические переменные, такие как координаты точек на некоторой оси, плоскости, поверхности и т.п.
3
Постановка и методы решения задачи Коши для уравнений первого порядка
Дифференциальное уравнение первого порядка записывается в виде
y' = f(x,y). |
(9) |
Общее решение этого уравнения, как уже было показано выше, имеет вид
y = ϕ(x,c1), |
(10) |
где функция ϕ(x,c1) является первообразной функцией для функции f(x,y).
В постановке задачи Коши для уравнения (9) начальное условие1, позволяющее определить значение константы c1, определяется заданием значения функции y в некоторой точке x0:
y(x0) = y0. |
(11) |
Относительно функции f(x,y) обычно делается предположение, что она определена, непрерывна и имеет непрерывную частную
производную |
∂ f в области интегрирования. Выполнение этих |
|
∂ y |
условий обеспечивает существование единственного решения, удовлетворяющего условию (11).
Аналитические решения в форме (10) могут быть получены лишь для сравнительно небольшого множества уравнений (9). Поэтому для произвольной функции f(x,y) в общем случае приходится искать решение, пользуясь каким-либо приближённым численным методом.
Численное решение задачи интегрирования дифференциаль-ного уравнения (9) определяется в виде таблицы значений y для дискретных значений аргумента х. Такая таблица вычисляется для значений аргумента хi, изменяющихся с постоянным шагом h
xi+1= xi + h для i=0, 1, 2, ...
Значение шага h определяется специалистом в зависимости от постановки решаемой задачи.
В точке х0 определено начальное значение y0. Наиболее простым методом определения значения y1(x1) в точке x1 = x0 + h при решении
1 В случае дифференциального уравнения первого порядка постановка задачи Коши совпадает с постановкой краевой задачи, т.к. для нахождения частного решения определяется только одно условие, которое можно считать как начальным, так и краевым.
4
задачи Коши является метод Эйлера, основанный на разложении функции y(x) в ряд Тейлора
yi+1 |
= y( xi +h) = y( xi )+ |
y' ( xi ) |
h + |
y"( xi ) |
h2 |
+...+ |
y( k )( xi ) |
hk +0( hk +1 ), |
(12) |
|
2! |
|
|||||||
|
1! |
|
|
|
k! |
|
|||
где 0(hk+1) - остаточный член формулы Тейлора, пропорциональный величине hk+1.
Ограничившись в формуле (12) первыми тремя членами, получим
y |
= y + |
y'i |
|
h + |
y"i |
h2 |
+0( h3 ). |
(13) |
||||||||||
|
|
|
||||||||||||||||
i+1 |
i |
1! |
|
|
2! |
|
|
|
|
|
|
|||||||
Используя (13) вычислим приращение функции y(x) на (i+1)-ом |
||||||||||||||||||
шаге |
|
|
|
|
|
|
|
|
|
|
|
y" |
h2 +0( h3 ) |
|
||||
yi = yi +1 − yi = fi h + |
(14) |
|||||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
Продифференцировав уравнение (9) получим |
|
|||||||||||||||||
y" |
= ∂f |
+ |
∂f |
y' = |
∂f |
+ f |
∂f |
(15) |
||||||||||
|
∂x |
|
|
∂y |
|
|
∂x |
|
|
∂y |
|
|||||||
Подставив (15) в (14), пренебрегая величиной 0(h3), получим |
|
|||||||||||||||||
|
|
|
|
1 |
|
∂f |
|
|
|
∂f |
|
2 |
|
|||||
yi = fi h + |
|
|
|
|
|
|
+ fi |
|
|
|
|
(16) |
||||||
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
∂x i |
∂y i |
h |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пренебрегая величиной 0(h2), получим |
|
|
yi +1 = yi + hf ( xi , yi ) |
( i = 0, 1, 2,...) |
(17) |
Эта формула позволяет последовательно вычислить |
значения |
|
y1, y2 , ..., yn, определяя тем самым искомое частное решение задачи Коши. Метод, использующий формулу (17) называется методом Эйлера.
Метод Эйлера имеет простой геометрический смысл. Так как f(xi,yi)= yi', то формула (17) определяет уравнение касательной к интегральной кривой в точке (xi, yi). Таким образом, в методе Эйлера на каждом шаге участок интегральной кривой заменяется отрезком касательной.
Рассмотрим пример решения методом Эйлера задачи Коши для
дифференциального уравнения |
|
|
|
|
y' = |
2 y |
, |
y( 1 ) =1 |
(18) |
|
x |
|
|
|
при изменении аргумента х на интервале [1; 1,5] с шагом h=0,1.
5
Вычисляя значения yi по формуле (17), получим следующие
значения: |
|
|
y0=1; |
|
|
y1= y0+h (2 y0/x0)=1+0,1*(2*1/1)=1,2; |
x1=x0+h=1+0,1= 1,1 |
|
y2=y1+h (2 y1/x1)=1,2+0,1*(2*1,2/1,1)=1,4(18); x2=x1+h=1,2 |
||
y3=y2+h (2 y2/x2)=1,418+0,1*(2*1,418/1,2)=1,6(54); |
x3=1,3 |
|
y4=y3+h(2y3/x3)=1,6(54)+ 0,2*1,6(54)/1,3=1,(90); |
x4=1,4 |
|
y5=y4+h(2y4/x4)=1,(90)+ 0,2*1,(90)/1,4=2,(18); |
x5=1,5. |
|
Точным решением дифференциального уравнения (18) является функция
y = x2. |
(19) |
(Продифференцировав уравнение (19) по x, получим y'=2x. Подставив (19) в уравнение (18), получим y'=2 y/x= 2* x2/ x=2x.)
Вычисляя значения yi, получим следующие значения yi: y0=1; y1=1,21; y2=1,44; y3=1,69; y4=1,96; y5=2,25.
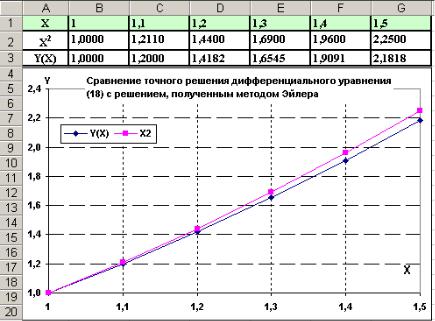
Ниже приведена итоговая таблица, позволяющая сравнить точное решение дифференциального уравнения (18) с численным решением этого же уравнения методом Эйлера.
Рис. 6.2. Таблица и диаграммы для сравнения результатов точного и численного решений дифференциального уравнения (18)
Очевидное расхождение результатов численного интегрирования и вычислений, выполненных по точной формуле, иллюстрирует факт существования погрешности при вычислениях,
6