
- •Г. В. Красоленко, н. В. Сванидзе, г. В. Якунина Обыкновенные дифференциальные уравнения. Ряды
- •Введение
- •Фамилия, имя, отчество
- •Примерный вариант контрольной работы № 5
- •Решение задачи № 1
- •Решение задачи № 2
- •Решение задачи № 3
- •Решение задачи № 4
- •Решение задачи № 5
- •Примерный вариант контрольной работы № 6 по теме « Ряды»
- •Решение задачи № 1
- •Решение задачи № 2
- •Решение задачи № 3
- •Решение задачи № 4
- •Решение задачи № 5
- •Контрольная работа № 5 по теме « Обыкновенные дифференциальные уравнения»
- •Контрольная работа № 6 по теме « Ряды»
- •Рекомендуемая литература
- •Оглавление
- •Обыкновенные дифференциальные уравнения. Ряды
- •190005, Санкт-Петербург, 2-я Красноармейская ул., д. 4.
Решение задачи № 2
Найдем решение уравнения

Это линейное уравнение, т.е. уравнение вида
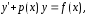
в котором предполагается, что функции
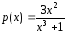 и
и
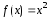
непрерывны в некотором интервале. Найдем его.
Функция
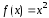 непрерывны при всех
непрерывны при всех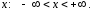
Так
как функция
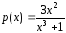 имеет точку бесконечного разрыва
имеет точку бесконечного разрыва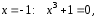 то она непрерывна на двух интервалах
то она непрерывна на двух интервалах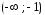 и
и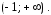
Мы
выбираем интервал
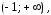 потому что наше решение должно
удовлетворять начальному условию
потому что наше решение должно
удовлетворять начальному условию

Точка
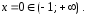
Следовательно,
дифференциальное уравнение (1) будем
рассматривать в полосе
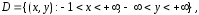 расположенной на плоскости
расположенной на плоскости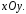 Тогда уравнение (1) удовлетворяет условиям
теоремы существования и единственности
решений (см. решение задачи №1 и [2], [4],
[5]). Поэтому через каждую точку
Тогда уравнение (1) удовлетворяет условиям
теоремы существования и единственности
решений (см. решение задачи №1 и [2], [4],
[5]). Поэтому через каждую точку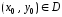 проходит единственная интегральная
кривая уравнения, определенная на
интервале
проходит единственная интегральная
кривая уравнения, определенная на
интервале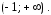
Существуют
различные способы нахождения общего
решения линейного уравнения. Мы рассмотрим
только один из них –
метод
Бернулли. Согласно этому методу будем
искать решение
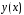 в виде произведения двух функций:
в виде произведения двух функций: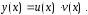
Подставим
функцию
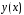 в уравнение (1). Опуская аргумент
в уравнение (1). Опуская аргумент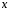 в функциях
в функциях и
и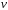 и учитывая, что
и учитывая, что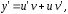 получаем
получаем
 или
или
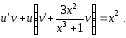
Выбирая
ненулевую функцию
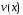 так, чтобы выражение, стоящее в скобках,
обращалось в нуль, приходим к решению
системы:
так, чтобы выражение, стоящее в скобках,
обращалось в нуль, приходим к решению
системы:
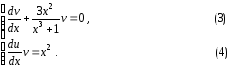
Уравнения
(3) и (4) являются уравнениями с разделяющимися
переменными в полосе
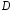 .
.
Разделим переменные в уравнении (3)
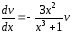 или
или
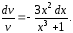
Интегрируя его, получаем
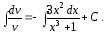
Положим
постоянную
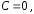 так как в качестве функции
так как в качестве функции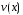 можно взять какое-либо ненулевое частное
решение уравнения (3).
можно взять какое-либо ненулевое частное
решение уравнения (3).
Вычисляя интегралы
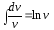 и
и
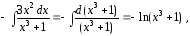
имеем
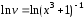 и
и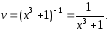
Найдем
общее решение уравнения (4). Подставляя
найденную функцию
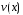 в уравнение (4), получим уравнение с
разделяющимися переменными
в уравнение (4), получим уравнение с
разделяющимися переменными
 или
или
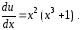
Разделяя переменные, найдем
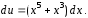
Отсюда
 или
или
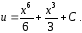
Общим
решением уравнения (1) в полосе
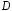 будет функция
будет функция
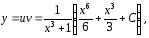
определенная
на интервале
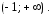
Используя
начальное условие (2), найдем частное
решение, интегральная кривая которого
проходит через точку с координатами
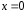 и
и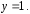
Для
этого подставим
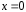 и
и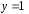 в
выражение (5) и найдем значение постоянной
в
выражение (5) и найдем значение постоянной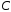 :
:
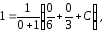
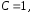
при котором из общего решения выделяется искомое частное.
Ответ.
Решением
задачи Коши (1),(2) является функция
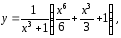 определенная на интервале
определенная на интервале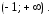
Решение задачи № 3
Найдем частное решение уравнения

удовлетворяющее начальным условиям
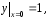

Данное
уравнение является «простейшим»
уравнением второго порядка, правая
часть которого зависит только от
независимой переменной
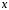 ,
т. е. уравнение вида
,
т. е. уравнение вида
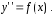
Предполагается,
что функция
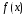 непрерывна в некотором интервале
непрерывна в некотором интервале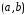 .
Тогда для простейшего уравнения
справедлива теорема существования и
единственности решения (см. [2] и [4]).
.
Тогда для простейшего уравнения
справедлива теорема существования и
единственности решения (см. [2] и [4]).
Для
уравнения (1)
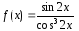 и с учетом начальных условий (2) мы
выбираем интервал
и с учетом начальных условий (2) мы
выбираем интервал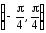 .
.
Тогда
на плоскости
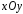 в интервале
в интервале
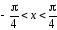 существует единственная интегральная
кривая уравнения (1), проходящая через
точку с координатами
существует единственная интегральная
кривая уравнения (1), проходящая через
точку с координатами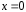 и
и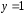 ,
при этом тангенс угла наклона касательной
в этой точке равен нулю (геометрический
смысл начальных условий (2)).
,
при этом тангенс угла наклона касательной
в этой точке равен нулю (геометрический
смысл начальных условий (2)).
Найдем решение задачи Коши (1), (2).
Учитывая, что
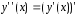 и
и
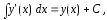
проинтегрируем
обе части уравнения (1) по переменной
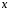 .
В результате получим
.
В результате получим
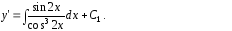
Для
вычисления интеграла сделаем замену
переменной
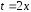 .
.
Отсюда
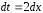 ,
,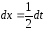 и
и
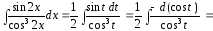
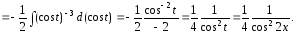
Таким образом,

Найдем
значение постоянной интегрирования
 ,
используя начальное условие
,
используя начальное условие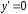 при
при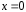 .
Учитывая, что
.
Учитывая, что ,
получаем
,
получаем
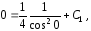
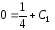 и
и
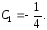
Подставим
значение
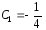 в уравнение (3)
в уравнение (3)

Интегрируя
обе части уравнения (4) по переменной
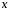 ,
получим
,
получим
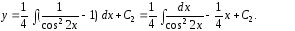
Для
вычисления интеграла вновь сделаем
замену переменной
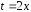 и
и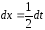 .
.
Тогда
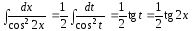
и, следовательно,
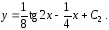
Найдем
значение постоянной интегрирования
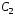 ,
используя второе начальное условие
,
используя второе начальное условие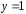 при
при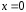 .
Учитывая, что
.
Учитывая, что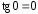 ,
получаем
,
получаем
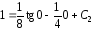 и
и
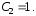
Отсюда искомое частное решение уравнения (1), удовлетворяющее начальным условиям (2), запишется в виде
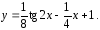
Ответ.
Решением
задачи Коши (1),(2) является функция
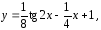 определенная на интервале
определенная на интервале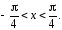
В задачах 4 и 5 даны линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и со специальной правой частью.
Уравнение вида

где
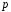 и
и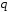 –
вещественные числа, а
–
вещественные числа, а
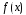 –
функция непрерывная на некотором
промежутке, называется линейным
уравнением второго порядка с постоянными
коэффициентами.
–
функция непрерывная на некотором
промежутке, называется линейным
уравнением второго порядка с постоянными
коэффициентами.
Функция
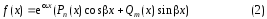
называется функцией специального вида.
Комплексные
числа
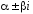 будем называть контрольными числами.
будем называть контрольными числами.
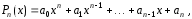
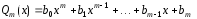
–многочлены
степени
 и
и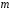 .
.
Функция
специального вида (2) определена при
всех
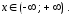
Уравнение
(1) называется неоднородным, если функция
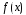 не равна тождественно нулю. Если же
не равна тождественно нулю. Если же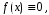 то уравнение (1) принимает вид
то уравнение (1) принимает вид

и называется однородным.
Если левые части однородного и неоднородного уравнений совпадают, то в этом случае однородное уравнение называется соответствующим данному неоднородному.
Имеет место следующее утверждение (см. [2], [4] и [5]).
Утверждение 1. ( О структуре общего решение неоднородного уравнения).
Если
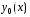 –
общее решение однородного уравнения
(3), а
–
общее решение однородного уравнения
(3), а
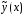 –
какое-либо частное решение неоднородного
уравнения (1), то
–
какое-либо частное решение неоднородного
уравнения (1), то

есть общее решение неоднородного уравнения (1).
Отсюда
следует, что построение общего решения
неоднородного уравнения состоит из
двух этапов. Сначала нужно найти общее
решение
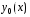 соответствующего однородного уравнения,
а затем найти какое-либо частное решение
соответствующего однородного уравнения,
а затем найти какое-либо частное решение неоднородного уравнения.
неоднородного уравнения.
Нахождение общего решения линейного однородного уравнения с постоянными коэффициентами (метод Эйлера)
Определение.
Будем говорить, что два решения
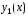 и
и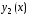 линейного однородного уравнения (3)линейно
независимы
на промежутке
линейного однородного уравнения (3)линейно
независимы
на промежутке
 ,
если их отношение
,
если их отношение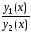 не равно тождественно константе.
не равно тождественно константе.
Тогда имеет место следующее утверждение.
Утверждение 2. ( О структуре общего решение однородного уравнения).
Если
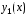 и
и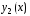 –
два линейно независимых решения уравнения
(3), то их линейная комбинация
–
два линейно независимых решения уравнения
(3), то их линейная комбинация
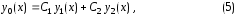
где
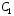 и
и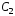 –
произвольные постоянные, есть общее
решение
линейного однородного уравнения (3).
–
произвольные постоянные, есть общее
решение
линейного однородного уравнения (3).
Решение уравнения (3)

где
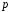 и
и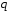 –
вещественные числа, будем искать в виде
–
вещественные числа, будем искать в виде

Постоянная
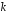 подлежит
определению.
подлежит
определению.
Так
как
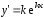 и
и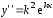 ,
то подстановка полученных выражений
производных в уравнение (3) приводит к
равенству
,
то подстановка полученных выражений
производных в уравнение (3) приводит к
равенству
 Так
как
Так
как
 ,
то последнее равенство выполняется,
если
,
то последнее равенство выполняется,
если

Таким
образом, функция
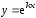 является решением дифференциального
уравнения (3), если постоянная
является решением дифференциального
уравнения (3), если постоянная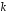 является корнем квадратного уравнения
(7).
является корнем квадратного уравнения
(7).
Уравнение (7) называется характеристическим уравнением дифференциального уравнения (3).
Напомним
формулу для определения двух корней
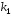 и
и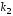 квадратного уравнения (7). Пусть
дискриминант
квадратного уравнения (7). Пусть
дискриминант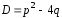 ,
тогда
,
тогда

При
решении квадратного уравнения (7) возможны
три случая в зависимости от знака
дискриминанта
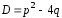 :
:
корни уравнения
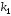 и
и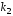 вещественные и различные
вещественные и различные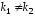
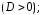
корни уравнения
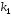 и
и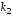 вещественные и равные
вещественные и равные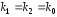
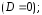
корни уравнения
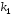 и
и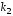 комплексно сопряженные числа
комплексно сопряженные числа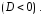
Рассмотрим каждый из этих случаев.
Корни уравнения
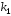 и
и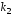 вещественные и различные
вещественные и различные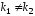 .
Тогда уравнение(3) имеет два решения
.
Тогда уравнение(3) имеет два решения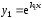 и
и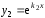 .
Они линейно независимы, так как
.
Они линейно независимы, так как
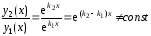
и, следовательно, общее решение уравнения (3) имеет вид

где
 и
и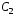 –
произвольные постоянные.
–
произвольные постоянные.
Пусть корни характеристического уравнения
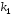 и
и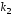 вещественные и равные
вещественные и равные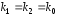 .
Тогда линейное однородное уравнение
(3) имеет два линейно независимых решения
.
Тогда линейное однородное уравнение
(3) имеет два линейно независимых решения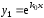 и
и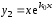 (см. [2] и [4]) и, следовательно, общее
решение уравнения (3) имеет вид
(см. [2] и [4]) и, следовательно, общее
решение уравнения (3) имеет вид

где
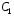 и
и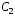 –
произвольные постоянные.
–
произвольные постоянные.
Пусть корни характеристического уравнения
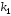 и
и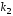 комплексно сопряженные числа
комплексно сопряженные числа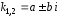 ,
где
,
где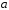 и
и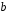 –
вещественные числа, причем
–
вещественные числа, причем
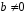 ,
, –
мнимая единица (см. [2] и [4]). Тогда линейное
однородное уравнение (3) имеет два
линейно независимых решения
–
мнимая единица (см. [2] и [4]). Тогда линейное
однородное уравнение (3) имеет два
линейно независимых решения
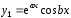 и
и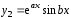 и, следовательно, общее решение уравнения
(3) имеет вид
и, следовательно, общее решение уравнения
(3) имеет вид
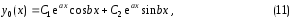
где
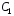 и
и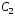 –
произвольные постоянные.
–
произвольные постоянные.
Построение частного решения линейного неоднородного уравнения со специальной правой частью. Метод неопределенных коэффициентов
Этот
метод применим тогда, когда в правой
части уравнения (1) стоит функция
специального вида (2). В этом случае
частное решение
 уравнения может быть найдено в соответствии
с видом его правой части.
уравнения может быть найдено в соответствии
с видом его правой части.
Рассмотрим здесь два частных варианта специальных правых частей.
Пусть в формуле (2) число
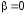 ,
тогда уравнение (1) имеет вид
,
тогда уравнение (1) имеет вид
 (12)
(12)
где
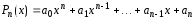 – многочлен степени
– многочлен степени
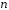 ,
а вещественное число
,
а вещественное число является контрольным числом.
является контрольным числом.
Уравнению (12) соответствует однородное уравнение
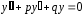
с характеристическим уравнением
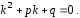 (13)
(13)
Пусть
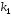 и
и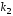 его корни.
его корни.
Имеет место следующее утверждение (см. [2]).
Утверждение 3.
Частное решение уравнения (12) следует искать в виде:
если контрольное число
 не является корнем характеристического
уравнения (13), т.е.
не является корнем характеристического
уравнения (13), т.е.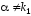 и
и
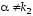 ,
то
,
то
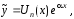
где
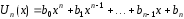 – многочлен той же степени
– многочлен той же степени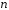 ,
что и многочлен
,
что и многочлен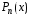 ,
с коэффициентами
,
с коэффициентами ,
подлежащими дальнейшему определению;
,
подлежащими дальнейшему определению;
если контрольное число
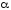 является простым корнем характеристического
уравнения (13), т.е.
является простым корнем характеристического
уравнения (13), т.е.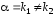 или
или
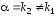 ,
то
,
то
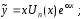
если контрольное число
 является кратным корнем характеристического
уравнения (13), т.е.
является кратным корнем характеристического
уравнения (13), т.е.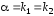 ,
то
,
то
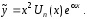
Приведем сводную таблицу.

где
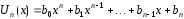 – многочлен той же степени
– многочлен той же степени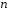 ,
что и многочлен
,
что и многочлен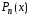 ,
с коэффициентами
,
с коэффициентами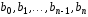 ,
подлежащими дальнейшему определению.
,
подлежащими дальнейшему определению.
Коэффициенты
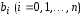 многочлена
многочлена должны быть такими, чтобы функция
должны быть такими, чтобы функция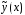 удовлетворяла уравнению (12). Поэтому
для их отыскания используют следующий
алгоритм.
удовлетворяла уравнению (12). Поэтому
для их отыскания используют следующий
алгоритм.
С
помощью утверждения
3
устанавливается вид частного решения
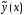 .
.
Затем
определяются производные
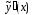 и
и .
Решение
.
Решение и его производные с неопределенными
пока коэффициентами подставляются в
уравнение (12) и обе его части сокращаются
на
и его производные с неопределенными
пока коэффициентами подставляются в
уравнение (12) и обе его части сокращаются
на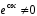 .
.
Далее,
мы определяем коэффициенты
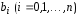 ,
исходя из тождественного равенства
двух многочленов, стоящих в левой и
правой частях уравнения (12)
,
исходя из тождественного равенства
двух многочленов, стоящих в левой и
правой частях уравнения (12)
(два
многочлена равны тогда и только тогда,
когда равны их коэффициенты при одинаковых
степенях переменной
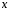 ).
).
