
- •Индивидуальное домашнее задание №1 по аналитической геометрии и векторной алгебре
- •Вариант I
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант i2
- •Вариант i3
- •Вариант i4
- •Вариант i5
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Индивидуальное домашнее задание №1 по аналитической геометрии и векторной алгебре
Количество баллов за задачи (суммарно 50 баллов):
1. 5 баллов
2. 5 баллов
3. 5 баллов
4. а),б),в) 3 балла за каждый пункт
5. 5 баллов
6. 5 баллов
7. 4 балла
8. 4 балла
9. 4 балла
10. 4 балла
Индивидуальное домашнее задание №1
по аналитической геометрии и векторной алгебре
Вариант I
1. Точка А (I; 4) является вершиной квадрата, а D (5; 1) – точкой пересечения диагоналей. Составить уравнения сторон квадрата.
2. Составить уравнения сторон треугольника АВС, зная две его вершины А (3;4 ), В ( I ; -I ) и точку пересечения медиан М ( I; 2 ).
3.
Провести прямую так, чтобы ее отрезок,
заключенный между двумя данными прямыми
![]() и
и![]() ,
делился в точке М (-I;
0) пополам.
,
делился в точке М (-I;
0) пополам.
4. Привести к каноническому виду и построить:
а)![]()
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
5.
Дана парабола
![]() .
Составить уравнение прямой, проходящей
через ее вершину параллельно прямой
.
Составить уравнение прямой, проходящей
через ее вершину параллельно прямой![]() .
.
6.
Найти угол между асимптотой гиперболы
![]() -
-![]()
![]() ,
проходящей черезI
и III
квадранты, и прямой, соединяющий фокус
параболы
,
проходящей черезI
и III
квадранты, и прямой, соединяющий фокус
параболы
![]() +
+![]() и центр окружности
и центр окружности![]() .
.
7. Найти
скалярное (![]() ,
,![]() ) и векторное
) и векторное![]() ,
,![]() произведения векторов. Координаты
точек А (0;2;1), В (3;1;2), С (-1; -1; 2) заданы в
декартовой системе координат.
произведения векторов. Координаты
точек А (0;2;1), В (3;1;2), С (-1; -1; 2) заданы в
декартовой системе координат.
8. Найти угол между прямыми
![]() и
и
![]() .
.
9. Составить уравнение плоскости, проходящей через прямую
![]() и перпендикулярной
плоскости
и перпендикулярной
плоскости
![]() .
.
10. Найти уравнение плоскости, проходящей через точки
А (3; 0; -1), B (1; 2; -4) и С (0; 7; -2).
Индивидуальное домашнее задание №1
по аналитической геометрии и векторной алгебре
Вариант 2
Найти вершины равнобедренного треугольника, если даны вершина прямого угла (3; 1) и уравнение гипотенузы
 .
.
Найти биссектрису того угла между прямыми
 и
и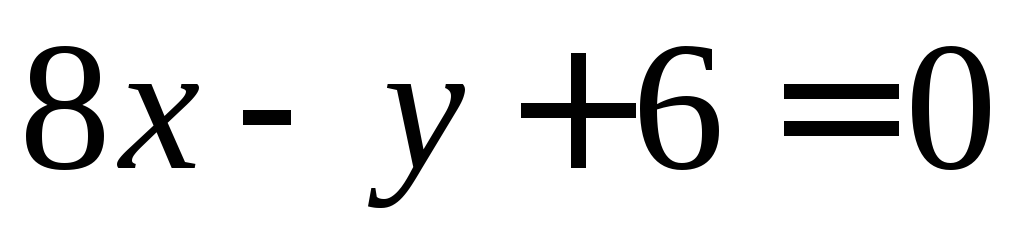 ,
в котором лежит начало координат.
,
в котором лежит начало координат.
Найти углы и площадь треугольника со сторонами
 ;
;
 .
.
Привести к каноническому виду и построить:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
5. Эллипс касается оси абсцисс в точке А (3;0) и оси ординат в точке
В (0;-4). Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.
6. Написать уравнение окружности с центром в фокусе параболы
![]() и радиусом, равным
фокусному расстоянию гиперболы
и радиусом, равным
фокусному расстоянию гиперболы
![]()
7. Найти скалярное
![]() и векторное
и векторное![]() произведения векторов.
произведения векторов.
Координаты точек А (2;5;-1), В (2;4;2), С (5;3;0) заданы в декартовой
системе координат.
8. Написать уравнение плоскости, проходящей через три точки А (1; 1; 0),
В (2; 0; 3) и С (0; -1; 2).
9. Написать уравнение перпендикуляра, опущенного из точки Р (3;1;1)
на прямую
![]() .
.
10. Найти угол
между прямой
![]() и плоскостью
и плоскостью
![]() .
.
Индивидуальное домашнее задание №1
по аналитической геометрии и векторной алгебре
