Вариант 9

1. На прямой найти точку, равноудаленную от начала координат и от прямой .

2. Привести к каноническому виду и построить:

а)

б)

в)

3. Найти уравнение прямой, проходящей через фокус параболы и центр окружности. Сделать чертеж.

4. Найти уравнение прямой, проходящей через правый фокус эллипса параллельно той асимптоте гиперболы, которая проходит через II и IV квадранты.

5. Найти скалярное и векторноепроизведения векторов. Координаты точекзаданы в декартовой системе координат.

6. Найти угол между плоскостями и.

7. Найти уравнение прямой, проходящей через точку и параллельной прямой.

Вариант 10

1. Найти уравнения сторон треугольника, зная одну из его вершин и уравнения двух высоти.

2. Привести к каноническому виду и построить:

а)

б)

в)

3. Найти острый угол между прямой, соединяющей правый фокус эллипса с точкойи асимптотой гиперболы, проходящей в I и III координатных углах.

4. Составить каноническое уравнение параболы с вершиной в точке и директрисой.

5. Найти скалярное и векторноепроизведения векторов. Координаты точекзаданы в декартовой системе координат.

6. Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости .

7. Показать, что прямая параллельна плоскости.

Вариант 11

1. Даны координаты вершин ромба ии уравнение одной диагонали. Найти уравнения сторон.

2. Привести к каноническому виду и построить:

а)

б)

в)

3. Найти острый угол между директрисой параболы и прямой, соединяющей левый фокус гиперболыс центром окружности.

4. Найти каноническое уравнение эллипса, если его малая полуось равна радиусу окружности , а правый фокус совпадает с центром другой окружности.

5. Найти скалярное и векторноепроизведения векторов. Координаты точекзаданы в декартовой системе координат.

6. Составить уравнение плоскости, проходящей через три точки ,и.

7. Найти угол между прямыми

и .

Вариант i2

1. В треугольникеданы: уравнение стороны, уравнение высоты, уравнение высоты . Написать уравнения сторон ,и третьей высоты.

2. Привести к каноническому виду и построить:

а)

б)

в)

3. Найти каноническое уравнение эллипса, проходящего через точку , если один из его фокусов находится в точке.

4. Через центр окружности провести прямую, параллельную прямой, соединяющей фокус параболыи левый фокус гиперболы.

5. Найти скалярное и векторноепроизведения векторов. Координаты точекзаданы в декартовой системе координат.

6. Доказать перпендикулярность прямых

и .

7. Составить уравнение плоскости, которая проходит через точку перпендикулярно двум плоскостями.

Вариант i3

1. Найти уравнение прямой, лежащей посередине между прямыми и.

2. Привести к каноническому виду и построить:

а)

б)

в)

3. Найти каноническое уравнение эллипса, если его эксцентриситет равен и эллипс проходит через точку.

4. Найти проекцию левого фокуса гиперболы на прямую, соединяющую фокус параболыс центром окружности.

5. Найти скалярное и векторноепроизведения векторов. Координаты точекзаданы в декартовой системе координат.

6. Найти тупой угол между прямыми: и.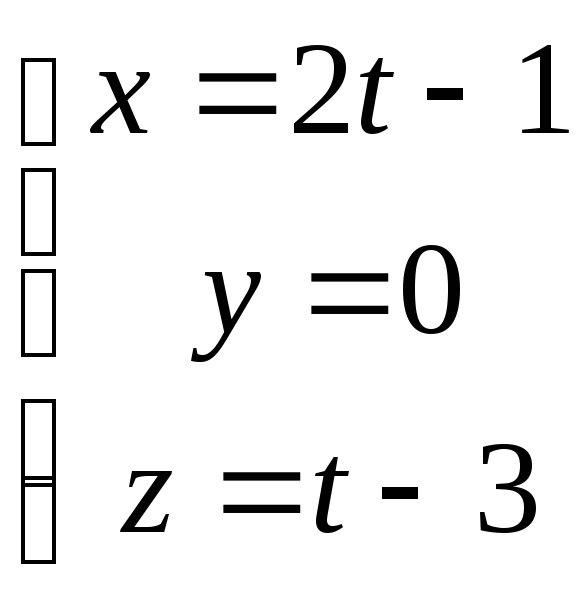

7. Написать уравнение плоскости, которая проходит через точку

и через прямую .