
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №5
- •Вариант №4
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №11
- •Вариант №12
- •Вариант №13
- •Вариант №14
- •Вариант №15
- •Вариант №16
- •Вариант №18
- •Вариант №17
- •Вариант №19
- •Вариант №20
- •Вариант №21
- •Вариант №22
- •Вариант №23
- •Вариант №24
- •Вариант №25
- •Вариант №26
- •Вариант №27
- •Вариант №29
- •Вариант №30
Вариант №11
Вычислить производную функции
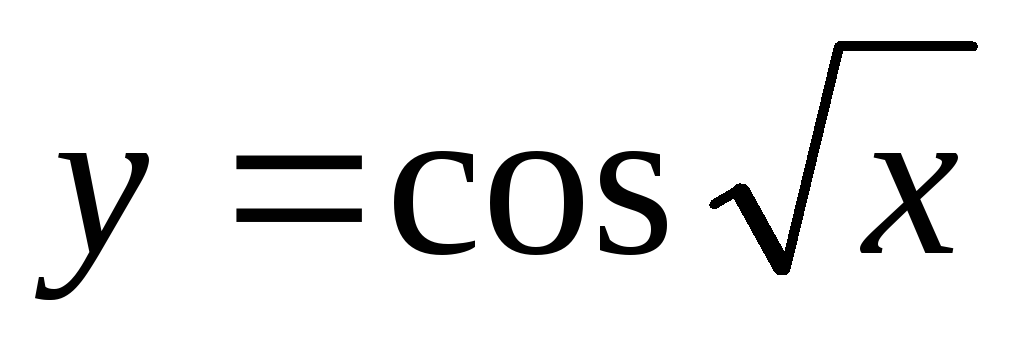 ,
используя определение.
,
используя определение.Вычислить производную по правилам дифференцирования:
а)
![]() ;
;
б)
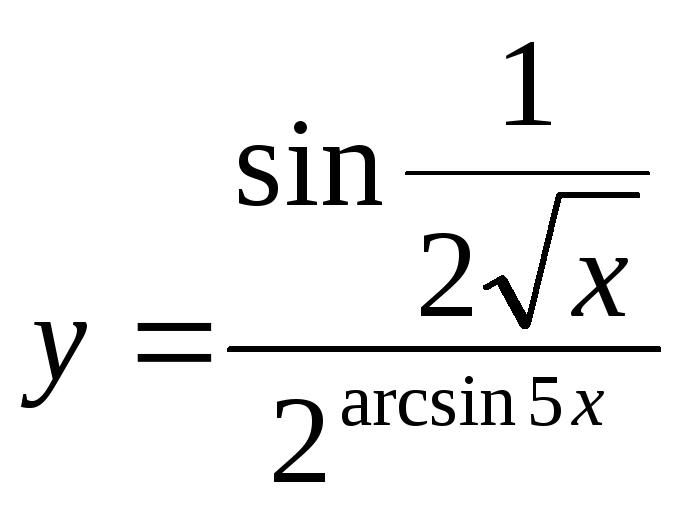 ;
;
в)
![]() ;
;
г)
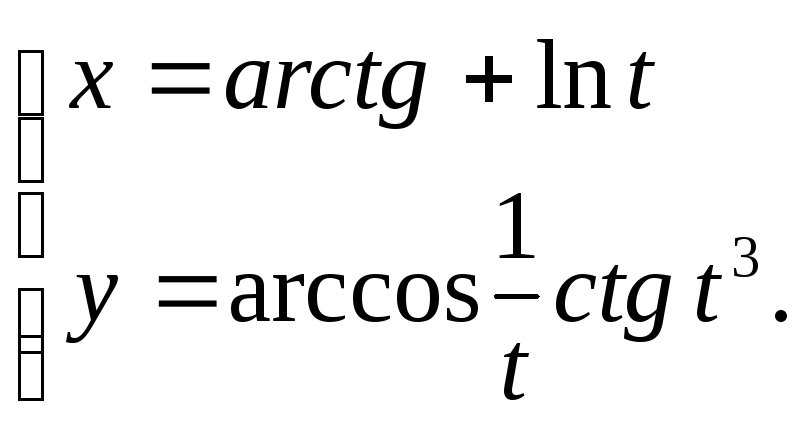
Написать уравнение нормали к кривой
 в точке пересечения её с осью 0Х.
в точке пересечения её с осью 0Х.Точка движется по логарифмической спирали
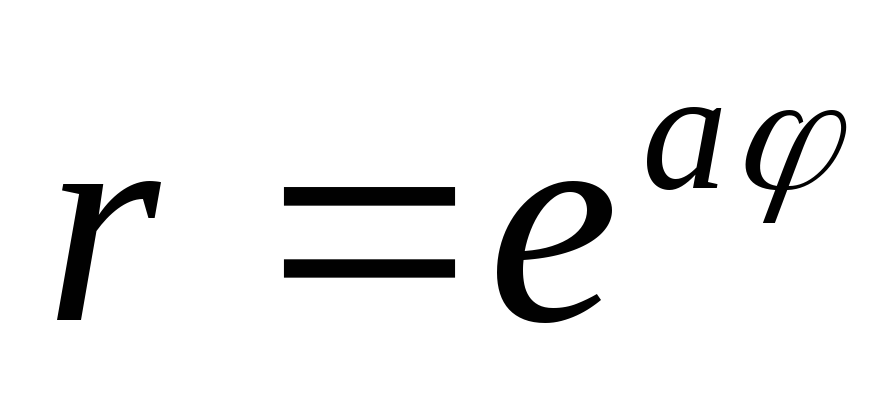 .
Найти скорость изменения полярного
радиуса, если известно, что он вращается
с постоянной скоростью
.
Найти скорость изменения полярного
радиуса, если известно, что он вращается
с постоянной скоростью .
.Показать, что функция
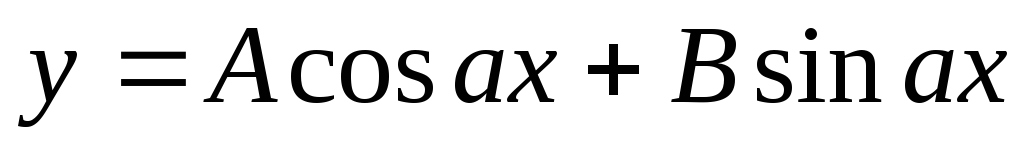 удовлетворяет
уравнению
удовлетворяет
уравнению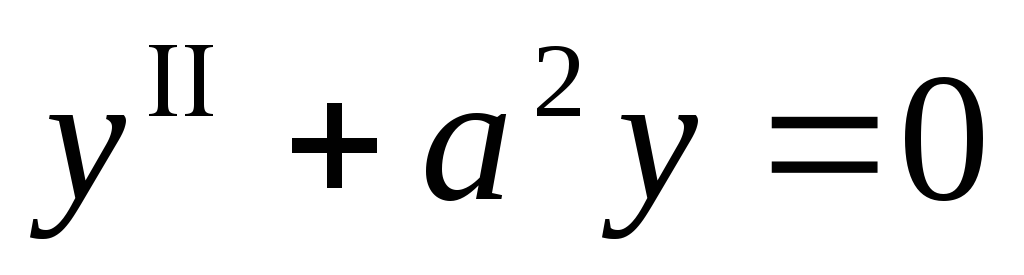 .
.Вычислить предел
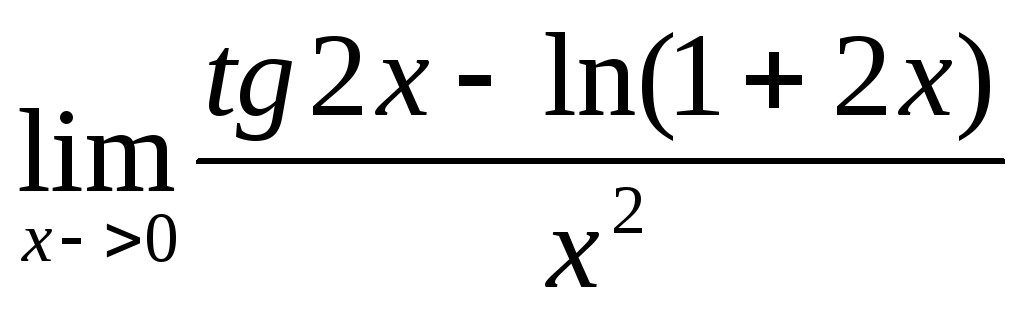 .
.Не находя производной функции
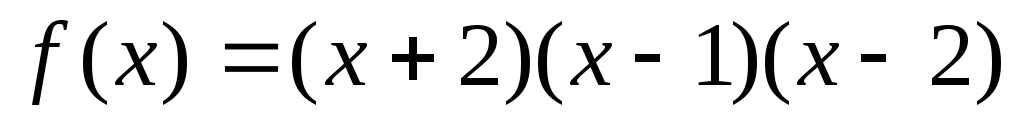 ,
выяснить, сколько действительных корней
имеет уравнение
,
выяснить, сколько действительных корней
имеет уравнение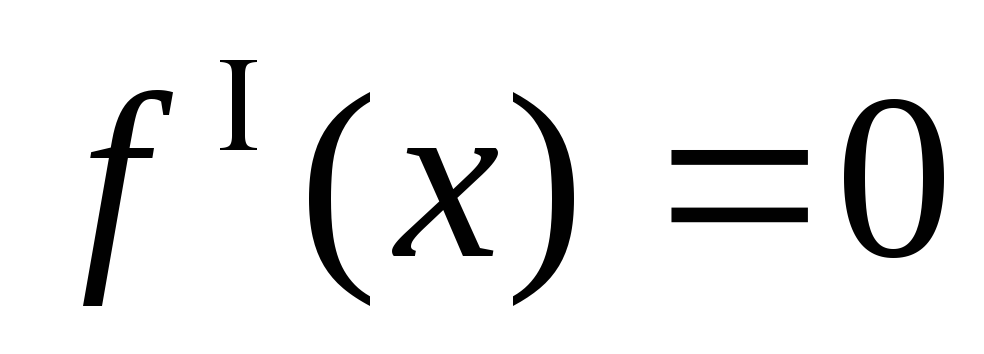 .
.Найти наибольшее и наименьшее значения функции
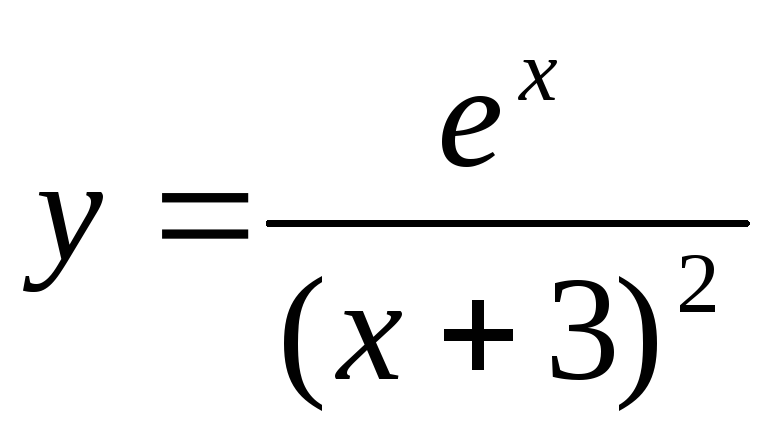 на промежутке [-2;0].
на промежутке [-2;0].
Вариант №12
Вычислить производную функции
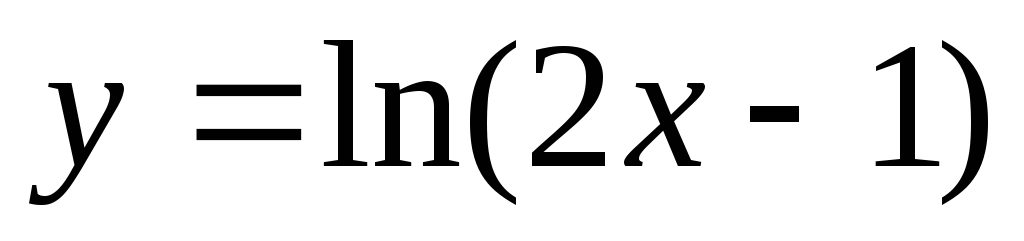 ,
используя определение.
,
используя определение.Вычислить производную по правилам дифференцирования:
а)
![]() ;
;
б)
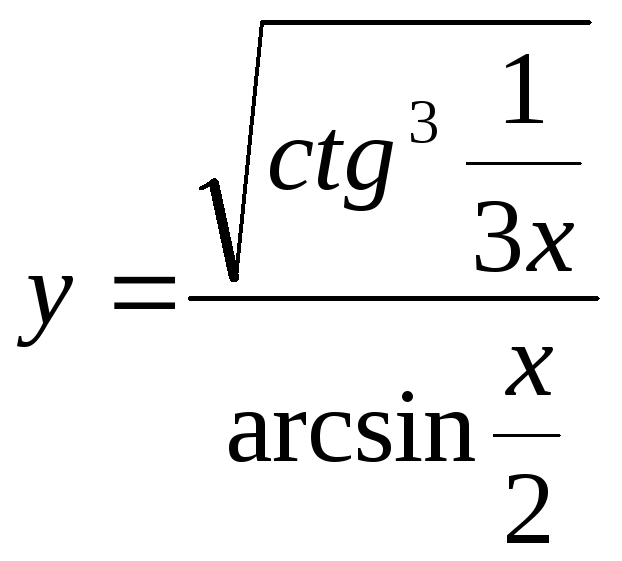 ;
;
в)
![]() ;
;
г)
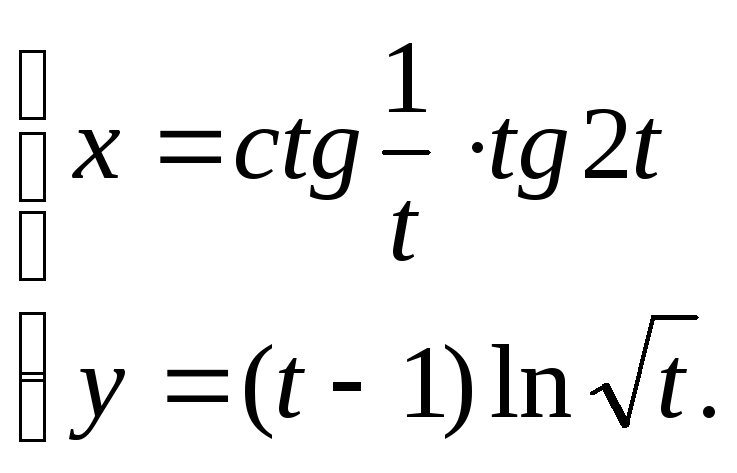
Написать уравнение касательной к кривой
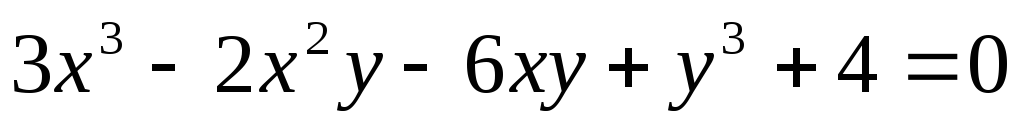 в точке М(1;1).
в точке М(1;1).По кубической параболе
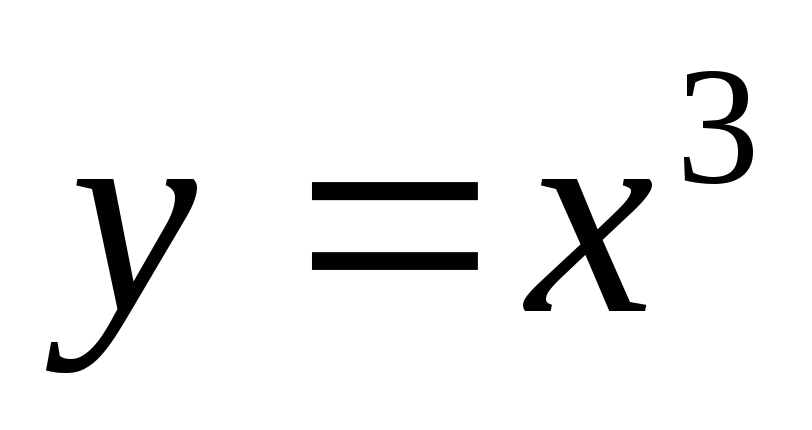 движется точка так, что её ординаты
изменяются в зависимости от времениt
по закону
движется точка так, что её ординаты
изменяются в зависимости от времениt
по закону
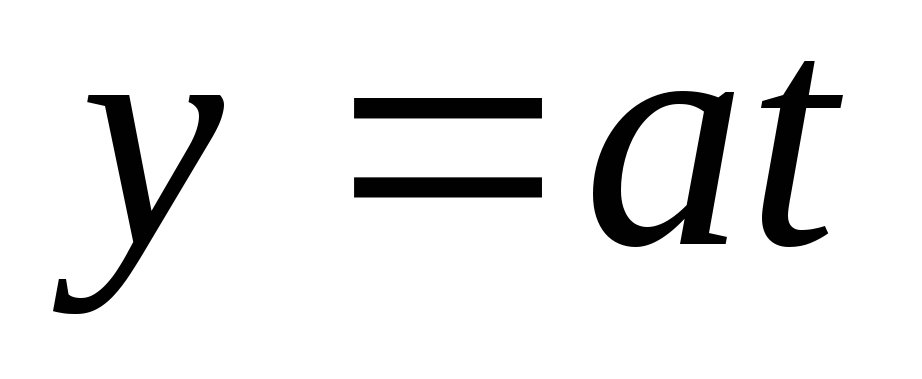 .
Найти скорость изменения абсциссы в
зависимости от времени.
.
Найти скорость изменения абсциссы в
зависимости от времени.Показать, что функция
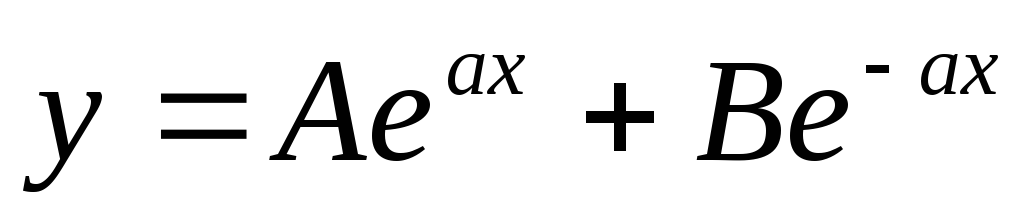 удовлетворяет уравнению
удовлетворяет уравнению
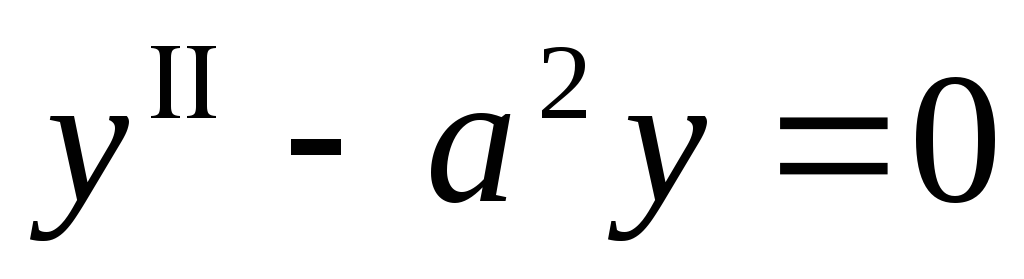 .
.Вычислить предел
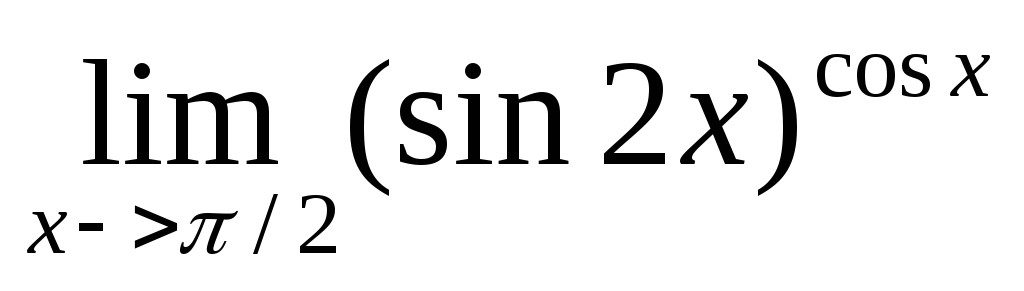 .
.Удовлетворяет ли функция
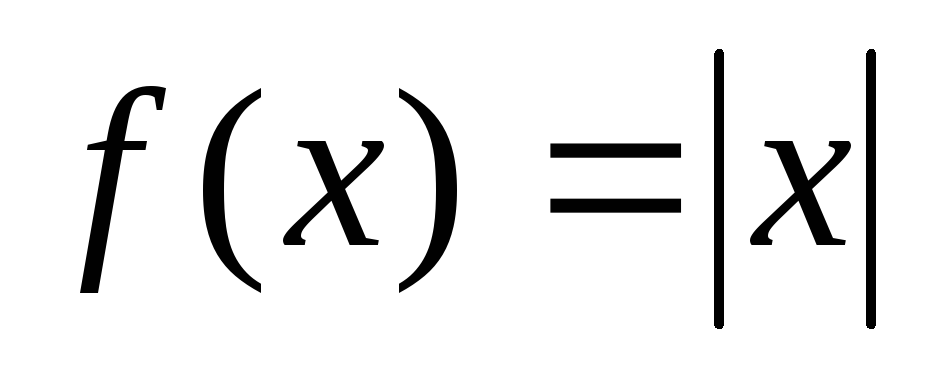 на промежутке [-2;2] условиям теоремы
Ролля. Пояснить графически.
на промежутке [-2;2] условиям теоремы
Ролля. Пояснить графически.Найти наибольшее и наименьшее значения функции
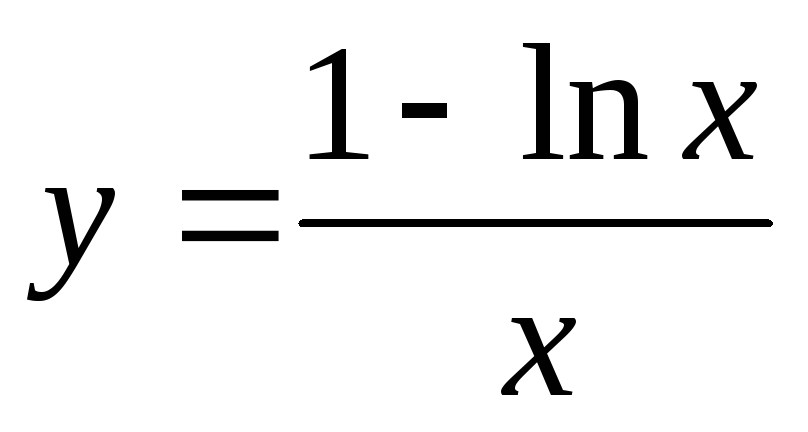 на
промежутке [1;10].
на
промежутке [1;10].
Вариант №13
Вычислить производную функции
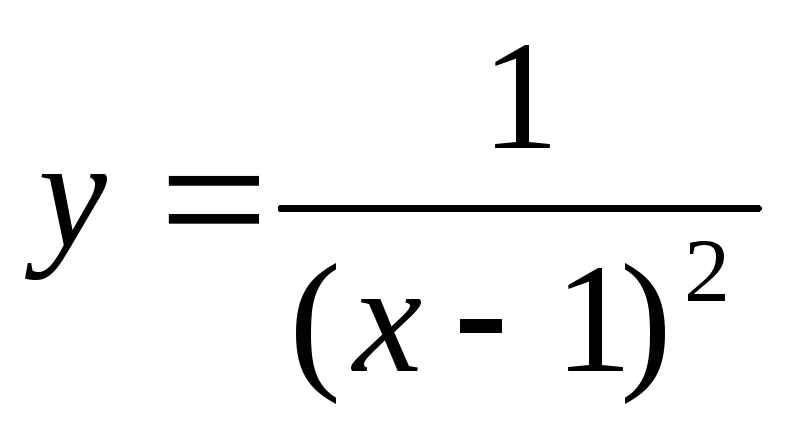 ,
используя определение.
,
используя определение.Вычислить производную по правилам дифференцирования:
а)
![]() ;
;
б)
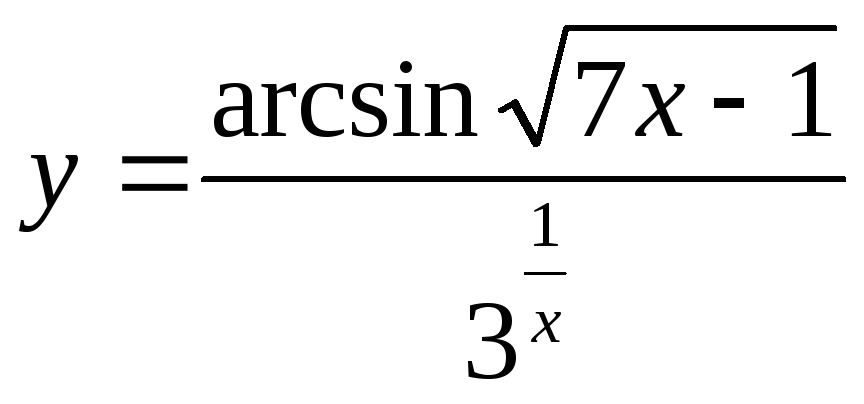 ;
;
в)
![]() ;
;
г)
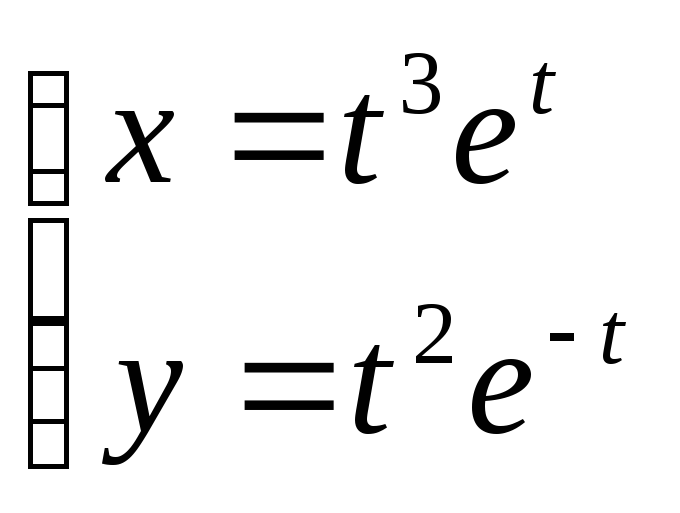
Написать уравнение нормали к кривой
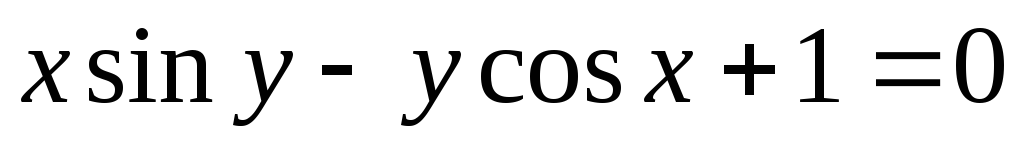 в точке пересечения её с осью 0У.
в точке пересечения её с осью 0У.В какой точке эллипса
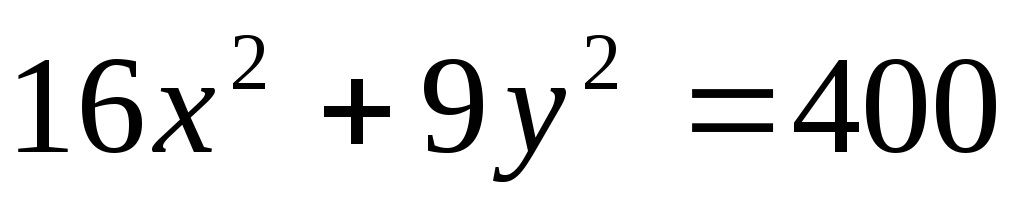 ,
ордината убывает с той же скоростью, с
которой абсцисса возрастает?
,
ордината убывает с той же скоростью, с
которой абсцисса возрастает?Показать, что функция
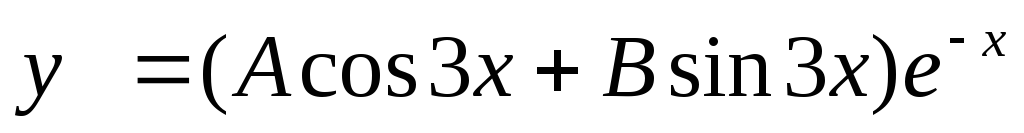 удовлетворяет
уравнению
удовлетворяет
уравнению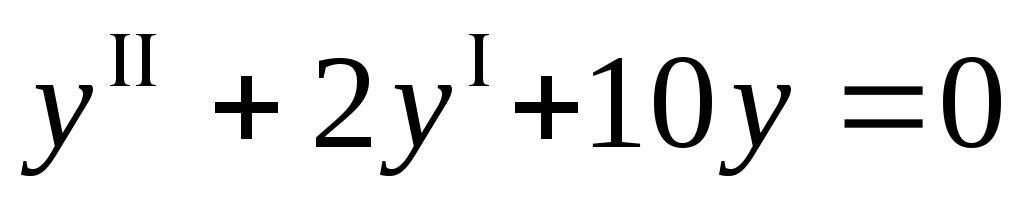 .
.Вычислить предел
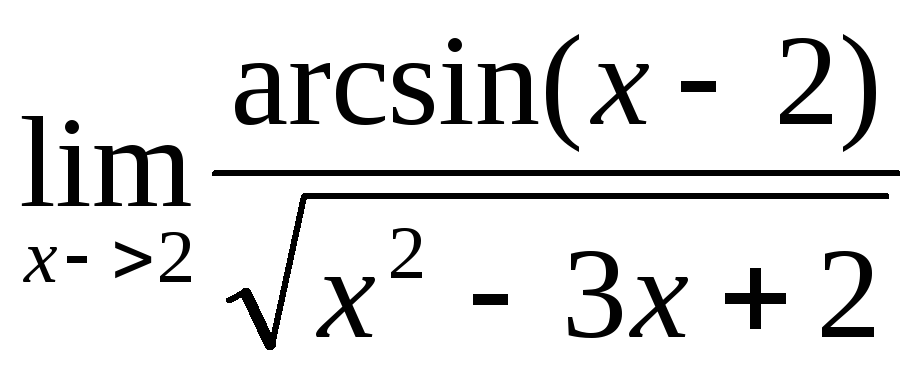 .
.Пользуясь формулой Лагранжа, доказать неравенство
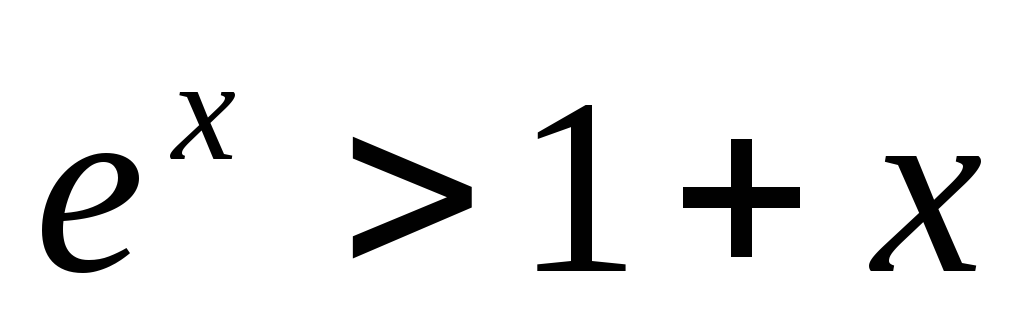 .
.Найти наибольшее и наименьшее значения функции
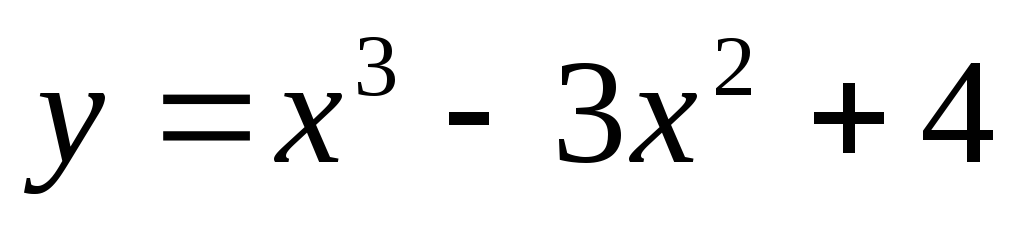 на
промежутке [-1;3].
на
промежутке [-1;3].
Вариант №14
Вычислить производную функции
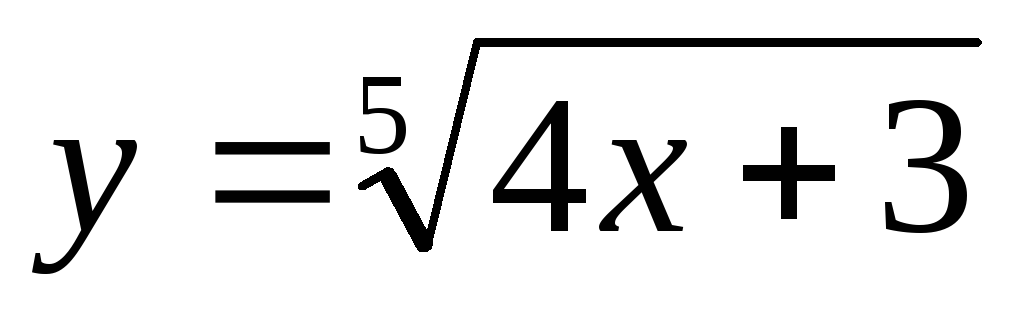 ,
используя определение.
,
используя определение.Вычислить производную по правилам дифференцирования:
а)
![]() ;
;
б)
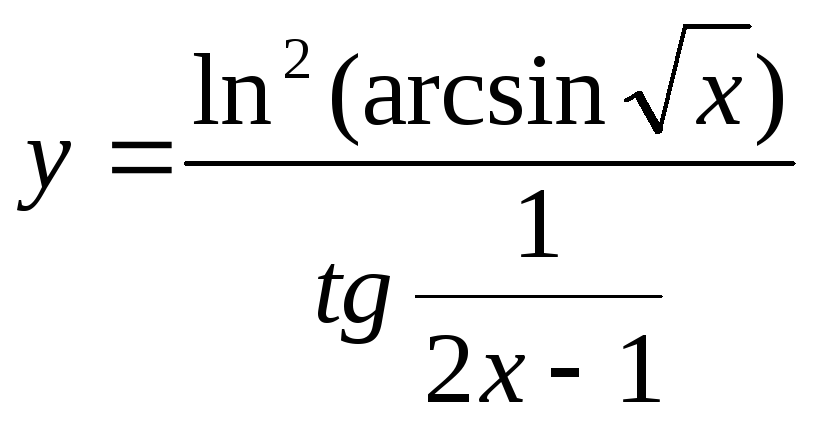 ;
;
в)
![]() ;
;
г)
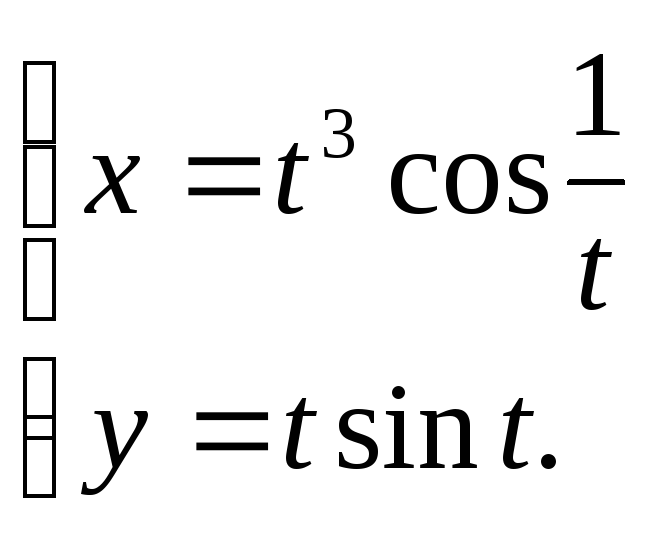
Написать уравнение нормали к кривой
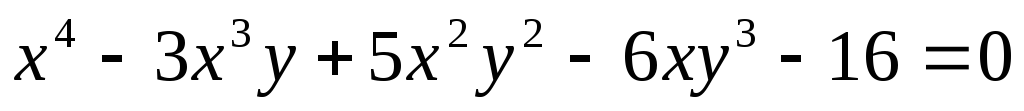 в точке её пересечения с осью 0Х.
в точке её пересечения с осью 0Х.Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за время T=8 секунд. Найти угловую скорость
 в момент времениt=32
секунд после начала движения.
в момент времениt=32
секунд после начала движения.Показать, что функция
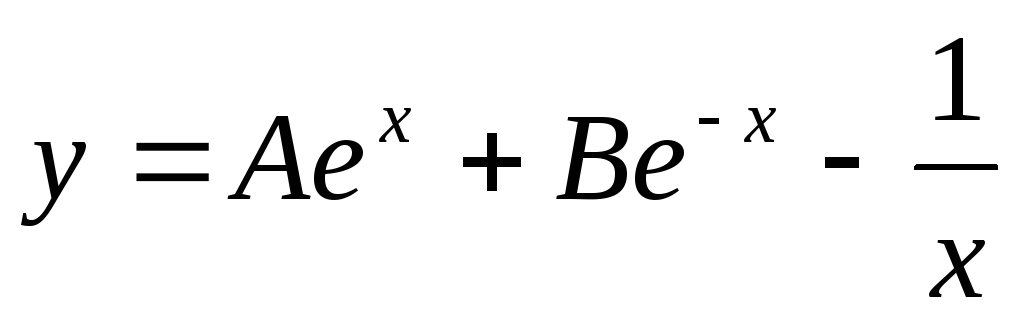 удовлетворяет уравнению
удовлетворяет уравнению
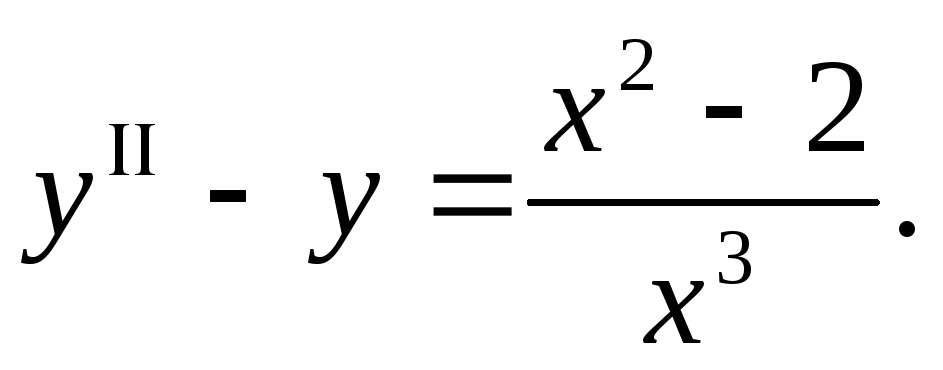
Вычислить предел
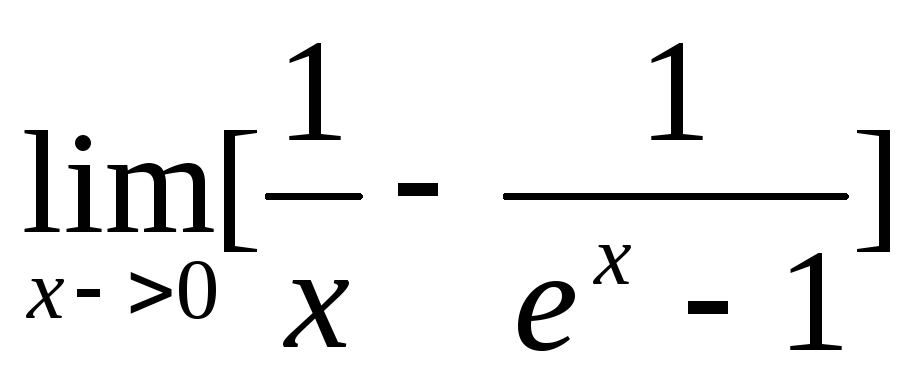 .
.Дана функция
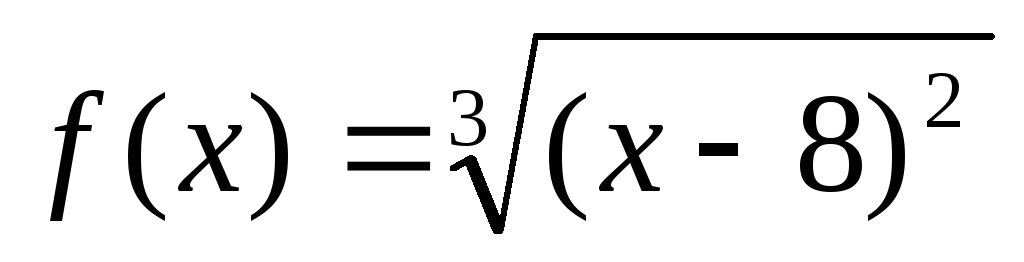 на отрезке [0;16]. Тогда
на отрезке [0;16]. Тогда
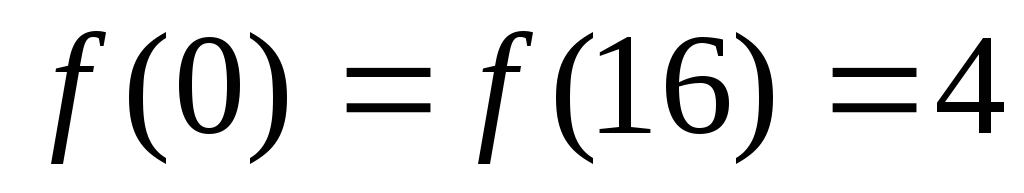 .
Однако производная
.
Однако производная
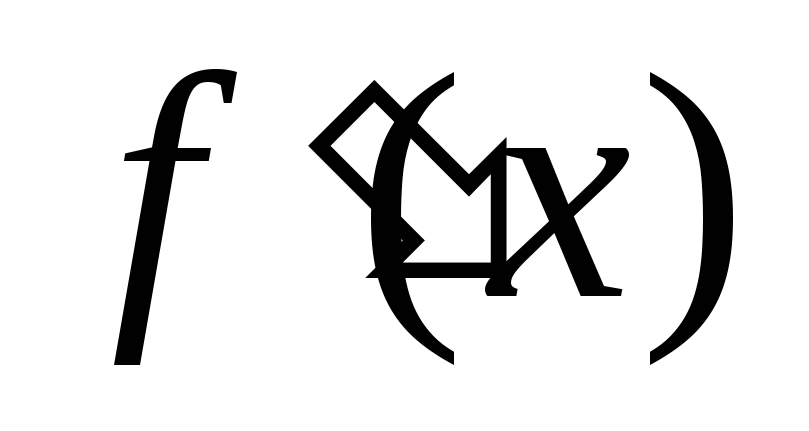 не обращается в нуль ни на одной точке
интервала (0;16). Противоречит ли это
теореме Ролля?
не обращается в нуль ни на одной точке
интервала (0;16). Противоречит ли это
теореме Ролля?Найти наибольшее и наименьшее значения функции
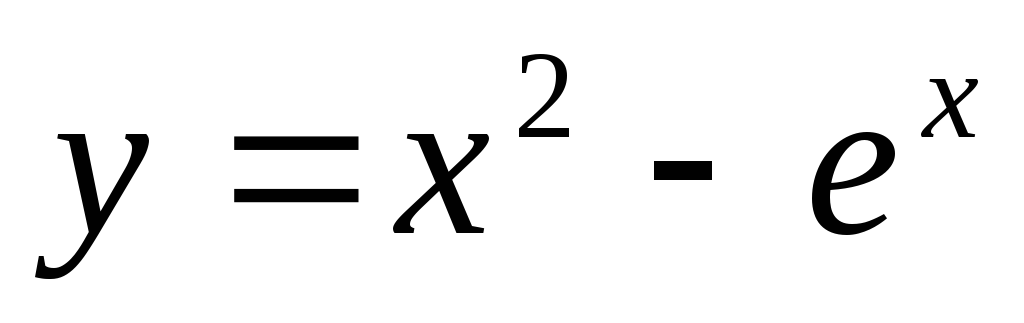 на
промежутке [-3;1].
на
промежутке [-3;1].
Вариант №15
Вычислить производную функции
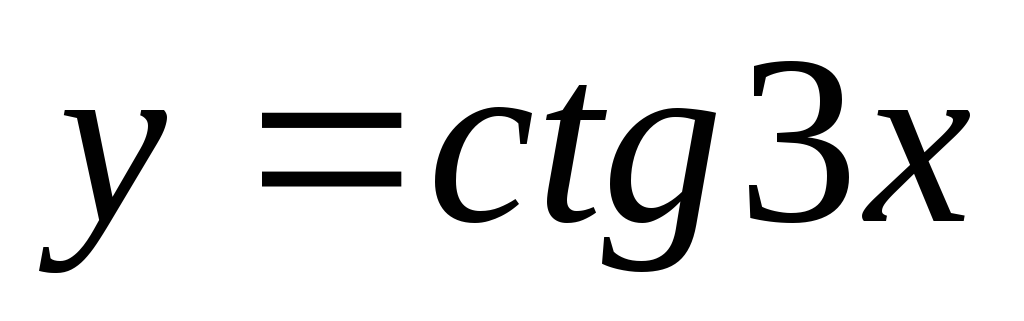 ,
используя определение.
,
используя определение.Вычислить производную по правилам дифференцирования:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
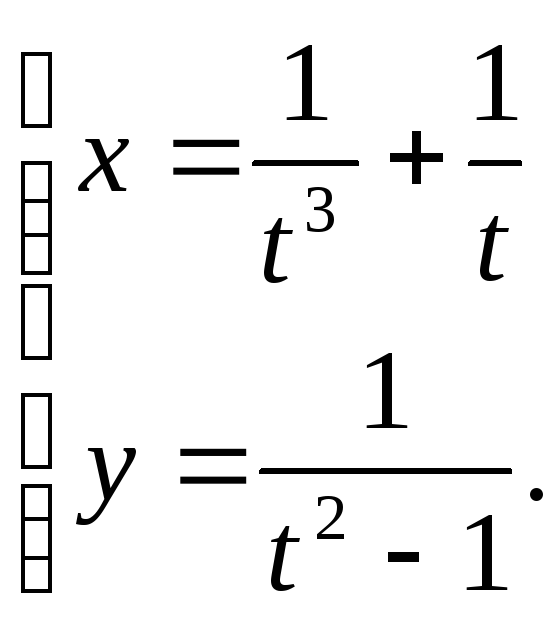
Какой угол с осью абсцисс образует касательная к кривой
 ,
проведенная в точке с абсциссой Х=1?
,
проведенная в точке с абсциссой Х=1?По параболе
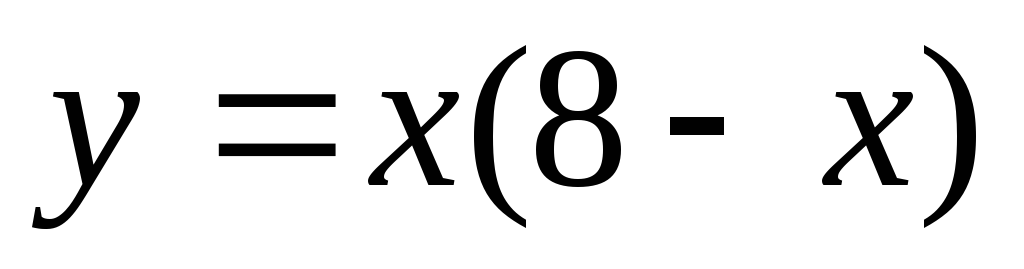 точка движется так, сто её абсцисса
изменяется в зависимости от времениt
по закону
точка движется так, сто её абсцисса
изменяется в зависимости от времениt
по закону
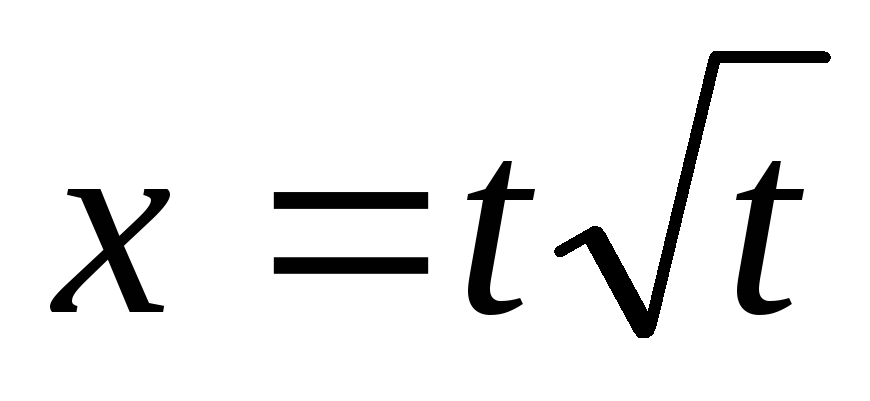 (t
- в сек.,x
- в м.). Какова скорость изменения ординаты
в точке М91;7)?
(t
- в сек.,x
- в м.). Какова скорость изменения ординаты
в точке М91;7)?Показать, что функция
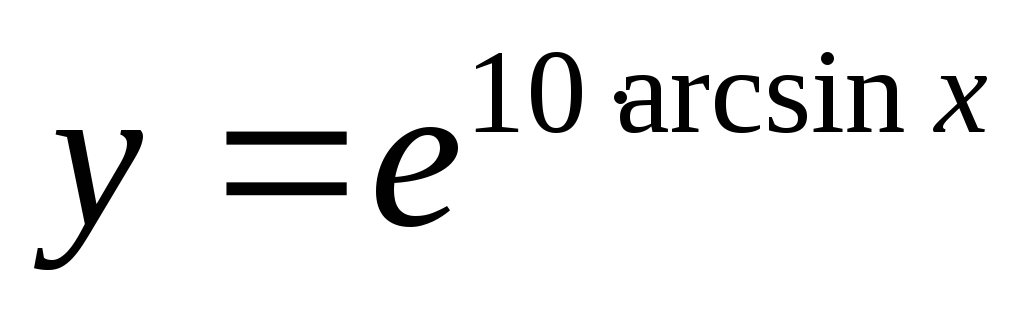 удовлетворяет
уравнению
удовлетворяет
уравнению
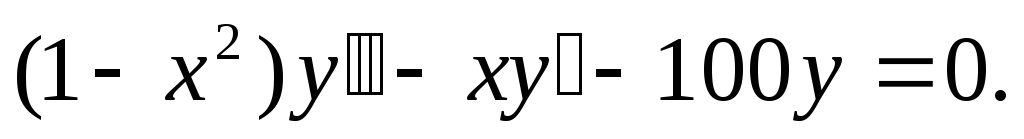
Вычислить предел
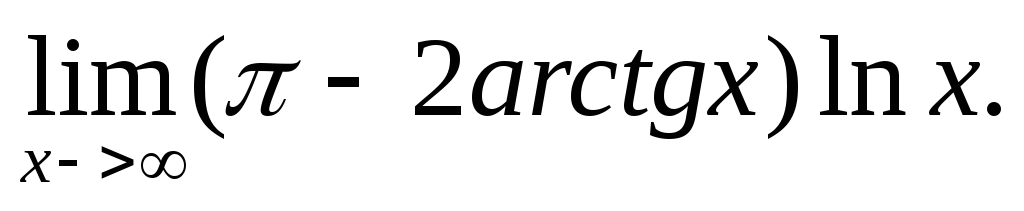
Написать формулу Лагранжа и найти точку С для функции
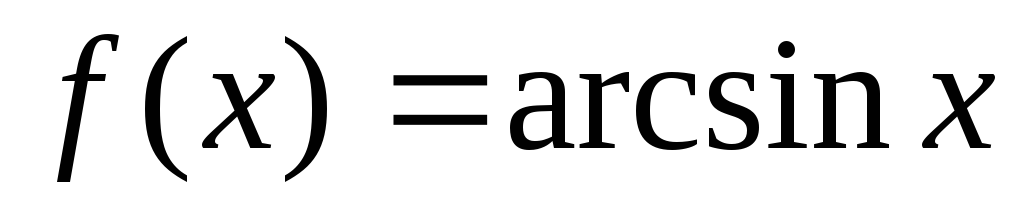 на
отрезке [0;1].
на
отрезке [0;1].Найти наибольшее и наименьшее значения функции
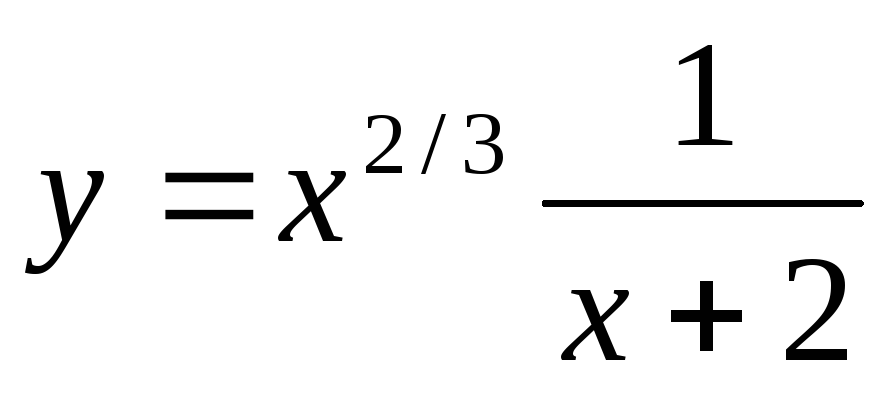 на
промежутке [0;5].
на
промежутке [0;5].
