38.Гомогенный химический процесс: простая необратимая реакция

Необратимая реакция A=R представлена химическим уравнением ⁿ (1),

Где n – порядок реакции по A; – концентрация А;r – скорость реакции. Зависимость r(C_A)

Видно, что от n зависит темп возрастания скорости – он выше для реакций более высокого порядка. Если C_A выразить через степень превращения X_A =>ⁿ (2)

Зависимость r(X_A)

Т.к. (3) то можно построить концентрационную и конверсионную зависимостьr(C_A) и r(X) скорости реакции при разных температурах T₁ и T₂ (T₂> T₁).

Видно, что при более высокой температуре превращение происходит быстрее. Так как из (3) следует, что увеличением температуры константа скорости реакции возрастает. Таким образом, повышение температуры обуславливает интенсификацию процесса для необратимой реакции. Ограничение температуры вызвано термостойкостью компонентов, появлением нежелательных реакций, возможностью самовоспламенения, устойчивостью материала аппаратуры и т.д.

39. Гомогенный химический процесс: простая обратимая реакция.

Обратимая реакция представлена кинетическим уравнением первого порядка в обоих направлениях: (1) Т.к. скорость реакции зависит от концентрации двух компонентов, зависимостьr(C_A) представлена рядом кривых, полученных при различных значениях . Точки С_АР – отвечают состоянию равновесия в реакционной системе, при этом концентрация компонентов равна С_АР и С_RP соответственно. Если С_А< С_АР, скорость реакции отрицательна (штриховая линия). Т.е. реакция протекает в обратном направлении.

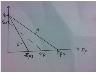
Выразим С_А и через степень превращения х:

Тогда: (2)

Зависимость r(x) имеет линейно убывающий вид (штриховая линия – зависимость r(x) для необратимой реакции). Из (2) следует, что r=0 при ; К_Р – константа равновесия; х_Р – равновесная степень превращения. увеличиваются с ростом температуры, но. Их совместное влияние зависит от соотношения энергий активации прямой и обратной реакции. Последнее различно для экзо- и эндотермических реакций.

Зависимость r(x) при температуре Т1 (штриховая линия) и при Т2>Т1 (сплошные линии). Если реакцию проводить при более высокой температуре, то начальная (при х=0) скорость увеличивается.

Далее равновесие изменяется в зависимости от типа реакции: для эндотермической реакции скорость повышается во всем интервале изменения х; в экзотермической реакции скорость повышается лишь до некоторого момента.

Т.о. для экзотермической реакции существуют оптимальные температуры для каждой степени превращения, при которой скорость реакции максимальна. Следовательно, уменьшение температуры по мере протекания реакции, приводящее к максимальной интенсивности данного процесса для обратимой экзотермической реакции.

Для обратимой эндотермической реакции оптимальная температура равна максимально допустимой.

Проведение процесса при максимально допустимой температуре определяет способ интенсификации процесса для обратимой эндотермической реакции.

40. Базисная система стехиометрических уравнений: стехиометрически независимые уравнения; выбор системы стехиометрических уравнений.

Стехиометрические уравнения показывают, в каких соотношениях реагенты вступают во взаимодействие. Они имеют вид:

где: А,B – исходные вещества; R,S– продукты реакции;

- стехиометрические коэффициенты.

Химические превращения могут быть описаны одним или несколькими стехиометрическими уравнениями. В случае, когда имеет место несколько стехиометрических уравнений, стехиометрический коэффициент i-го вещества, j-го уравнения, можно обозначить, как и систему уравнений можно представить в виде:

, где n – число реагентов, m – число уравнений , – для исходных реагентов,– для продуктов,– для i-го вещества, не входящего в j-ое уравнение.

Совокупность стехиометрических уравнений, однозначно и полно описывающих процесс, называют базисной системой стехиометрических уравнений. Так как со стехиометрическими уравнениями можно делать линейные преобразования (складывать уравнения, переносить члены справа налево и наоборот и т.д.), то возникают трудности при определении базисной системы уравнений, например: процесс получения водорода из природного газа можно записать двумя уравнениями:

но можно эти уравнения сложить и тогда:

Для расчета данного процесса не достаточно последнего уравнения, хотя оно и является суммой предыдущих. Таким образом, базисная система линейно-независимых стехиометрических уравнений, однозначно описывающих процесс, должна включать все участвующие в химическом превращение вещества и не должна включать ни одного уравнения, которое может быть получено линейными преобразованиями других.

В большинстве случаев необходимое число стехиометрических уравнений можно определить по формуле: У=В-Э, где У - число независимых уравнений, В - число веществ (реагентов), Э- число химических элементов из которых состоят реагенты. Так для конверсии метана В=5 ; Э=2 , откуда У=2. Базисная система включает два уравнения. Для отдельных обменных процессов формула имеет вид: У=В-Э+1.