70. Неизотермический процесс в химическом реакторе. Режимы идеального смешения периодический и идеального вытеснения с теплообменом. Сопоставление адиабатического процесса и изотермическим.
Допустим,
изотермический процесс осуществляется
при температуре адиабатического
экзотермического процесса и превышающую
ее в эндотермическом процессе.
= .
(.
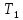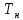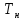- температура на входе в реактор). В
первом случае изотермический процесс
будет менее интенсивным, чем адиабатический,
а во втором большая степень превращения
будет достигаться при меньшем времени
реакции.
Если
же температура изотермического процесса
.
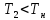то интенсивность изотермического
процесса будет выше, чем адиабатического,
и это будет наблюдаться до тех пор, пока
возрастающая в течение реакции температура
не достигнет .
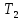(для экзотермической реакции)
В
эндотермическом процессе при
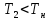картина будет обратной. Если реакция
обратимая, то общий характер зависимости
степени превращения Х и температуры Т
от
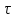(условного времени реакции сохраняется,
с отличием лишь в том, что процесс будет
протекать только до равновесной степени
превращения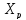
.
Тогда максимальный разогрев будет:
Т-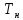
=
]
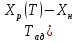(4)
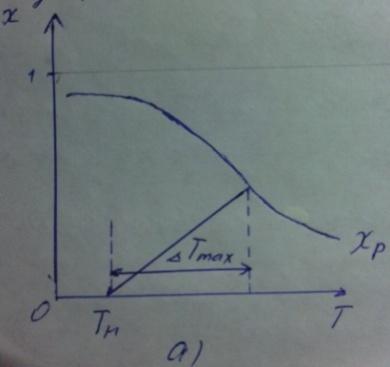
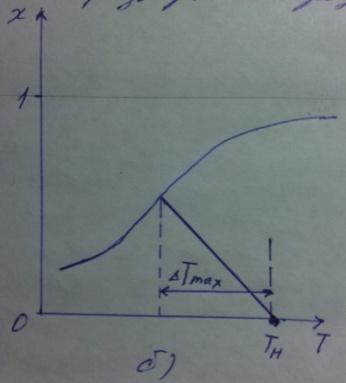
Значения максимального разогрева определяют из графика «Т-Х»
Зависимость
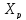и
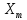для адиабатического процесса.
Определение
максимального адиабатического разогрева
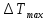при протекании обратимых а)экзотермической
и б) эндотермической реакции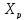
- равновесные степени превращения;
прямые – адиабаты в режиме ИВ.
Пересечение
кривых зависимостей
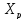(Т)
и Х(Т) адиабатического процесса
соответствует максимальному нагреву
в слое -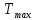
как показано на рисунке а) и б).
Интерпритация результатов исследования
модели на реальный объект.
Исследованная модель описывает процесс в реакторах ИВ и идеального смешения периодическом ИС-п.
В
первом случае зависимости Х (
)
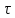и Т(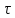
) (степени превращения и температуры от
условного времени реакции) описывают
изменение Х и Т по длине реактора, не
меняющегося во времени протекания
реакции.
Во – втором изменение во времени Х и Т распределение которых по объему реактора в каждый момент времени одинаковы.
71. Неизотермический процесс в химическом реакторе. Температурный режим в проточном реакторе идеального смешения. Анализ процесса.
Математическая модель процесса.
Сi-Ci0/Ԏ=Wi(C,
Т) (1)
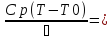Qpr(c,Т)-Кt
Fуд(Т-Тx)
Тx – температура теплоносителя; Кt – коэффициент теплопередачи;
Fуд=
- удельная поверхность теплообмена (FT
– площадь поверхности теплообмена; VP
– объем реактора);
Ԏ=
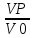– условное время реакции (V0
– объем потока реагентов, входящих в
реактор в единицу времени); Сp
– теплоемкость;
x=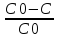
- степень превращения.
Используя
выражения для адиабатического разогрева
∆Tад=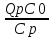
;
параметра
теплоотвода B=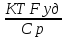
;
и отношения скорости реакции к исходной
концентрации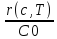
=
r(x,Т)
получим из (1):
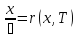(2)
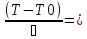∆Tад
r(x,Т)-B(Т-Тx)
В адиабатическом режиме (B=0) получим:
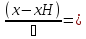r(x,Т)
(3)
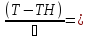∆Tад
r(x,Т)
(xH – степень превращения на входе в реактор)
С0 – начальная концентрация исходного компонента в непрореагировавшей смеси и CH – концентрация исходного компонента на входе в реактор не всегда одинаковы. Если в реактор подается частично прореагировавшая смесь xH≠0. Разделив второе уравнение на первое в (3) получим:
(T
– TH)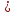
∆Tад(x
– xH)
(4), отсюда, Температура
и степень превращения в реакторе будут
иметь ступенчатое распределение
профили
степени превращения x(Ԏ)
и температуры T(Ԏ)представлены
на рис 1а и 1б соответственно.
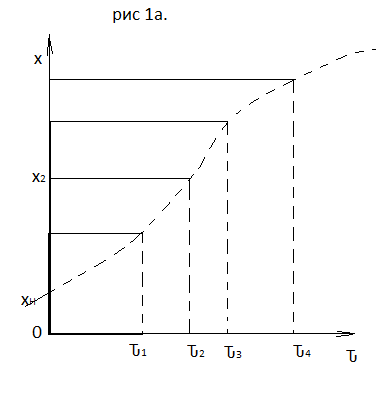
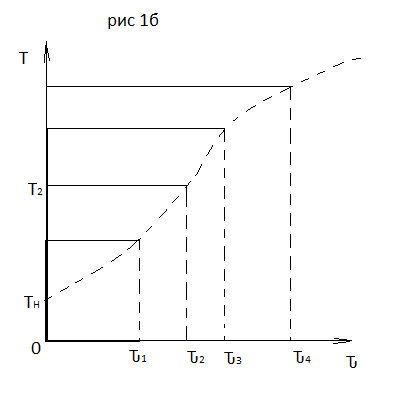
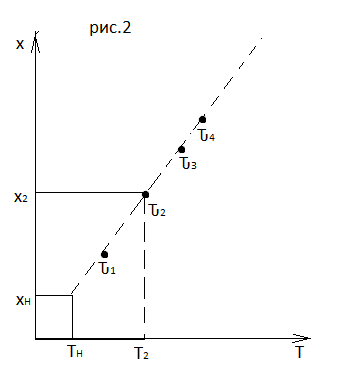
Кривые х(Ԏ) и Т(Ԏ) есть графическое отображение функции (4), и эти зависимости надо представлять, как набор значений x и Т устанавливаются в различных реакторах. В координатах «T – x» режим процесса в реакторе будет описываться линией, соединяющей две точки между исходным состоянием смеси при Ԏ, то есть последовательность точек при разных Ԏ будет лежать на прямой адиабаты T=TH+∆Tад(x – xH) (см.(4)), показанной на рис.2 штриховой линией.
График «Т – х» для проточных реакторов ИС-н с различными значениями условного времени Ԏ (реакция экзотермическая) представлен на рис.2.