59. Классификация процессов в химическом реакторе и их математических

Моделей.Следует следующая классификация химических реакторов:

1. Организация материальных потоков.

   1. Поток в реакционной зоне.

      1. Реактор идеального вытеснения.

      2. Реактор идеального смешения.

      3. Реактор неидеальный.

1.2.1. Проточный реактор (непрерывный).

1.2.2. Непроточный реактор (периодический).

2. Организация тепловых потоков.

2.1. Температурный режим процесса.

2.1.1. Изотермический.

2.1.2. Неизотермический.

2.2. Тепловой режим реактора.

2.2.1. Адиабатический.

2.2.2. С внешним теплообменом.

62.Изотермический процесс в химическом реакторе. Режим идеального смешения периодического и идеального вытеснения. Простая обратимая реакция а↔ r

Математическая модель процессов:

dc/d ῖ =W (с);с=с₀ ,при ῖ =0 (1)

Где ῖ= ῖ ; t в зависимости от процесса.

Скорость реакции r(c)=k₁c_A-k₂c_B зависит от концентраций с_А и с_В, следовательно для описания процесса используют два уравнения вида (1) .

Перейдем к одной переменной – степени превращения х реагента А: с_А=с₀(1-х) и c_R=c₀x ,где с₀-исходная концентрация реагента А.

Модель процесс примет вид :

dx/dῖ=k₁(1-x)-k₂x ; х=0 ,при ῖ =0 (2)

Преобразуем (2) к виду dx/dῖ=k₁ -(k₁+k₂)x и проинтегрируем его :

ln k₁-(k₁+k₂)x-ln k₁/k₁+k₂=ῖ , или х =k₁/k₁+k₂ [1-e^{-(k1+k2) ῖ} ] (3)

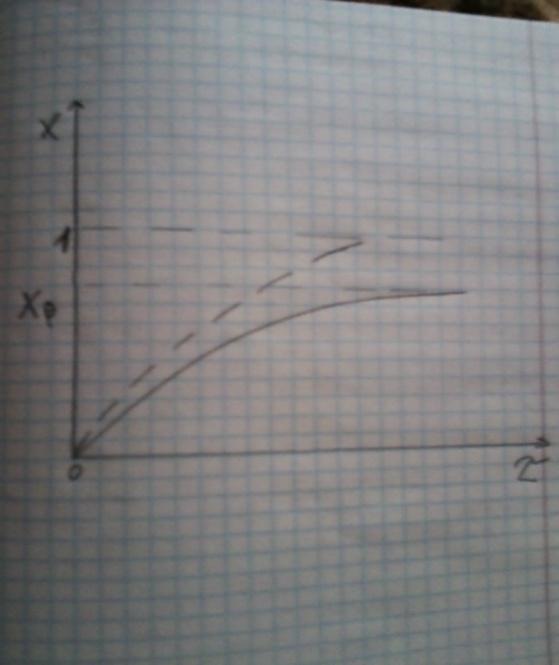
Из (3) видно ,что с увеличением ῖ х(ῖ) увеличивается вплоть до х=k₁/k₁+k₂ при ῖ→∞.

Т.к.константа равновесия обратимой реакции K_р=k₁/k₂ и равновесная степень превращения x_р =K_р/1+K_р, то предельное превращение достигаемое в реакторе равно :

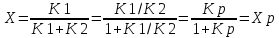(4)

Это естественно ,т.к реакция протекает до равновесия .Зависимость х(ῖ) для простой обратимой реакции (сплошная линия ) и обратимой реакции (штриховая линия ) представлена на рисунке.

Рассматриваемая реакция имеет первый порядок в прямом и обратном направлении ,поэтому начальная концентрация с₀ не влияет на степень превращения .

60. Анализ процесса в химическом реакторе.

Анализ процесса в химическом реакторе исследования влияния условий процесса и характеристик( свойств) его составляющих на показатели работы реактора, а также выявление особенностей процесса и режима.

Условия процесса – состав исходной реакционной смеси ( исходные концентрации реагентов 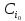), объем поступающего потока ( нагрузка на реактор 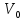), температуры входного потока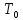, хладагента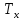( для процессов с теплоотводом) или в реакторе ( для процессов с теплоотводом) или в реакторе ( для изотермического процесса –).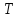

Режимы процесса – характеристики химического процесса, схема превращения и тип реакций( вид кинетических уравнений), энергия активации, тепловой эффект; для неизотермических процессов – параметры теплоотвода ( коэффициенты теплопередачи 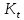, величина поверхности теплообмена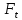, теплофизические свойства потока).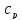

Показатели процесса – степень превращения x, селективность – S, выход продукта E, а также профили концентраций, степени превращения и температуры в реакторе, их изменение во времени. Зная эти показатели, можно далее определять и другие: конструктивные параметры реактора, энергетические затраты, экономические показатели и др.

Особенности процесса и режима – влияние условий и свойств процесса на его показатели, управление процессом ( изменение условий и свойств для достижения желательных показателей); критические режимы ( например, их существование , неустойчивость).

Анализ процесса в химическом реакторе осуществляют с использованием методов математического моделирования.

Один из вариантов последовательности проводимого анализа рассмотрим ниже.

1. Обоснование и построение математической модели процесса.

2. Преобразование уравнений математической модели к виду, удобному для дальнейшего исследования.

3. Решение уравнений математической модели для получения зависимостей, подлежащих анализу.

4. Представление результатов решения уравнений в графическом виде, как наиболее удобном для анализа.

5. Интерпретация результатов решения уравнений на процесс в исследуемом реакторе, то есть перенос полученных зависимостей между переменными уравнений на состояние процесса в реакторе.

6. Собственно анализ модели и процесса: выявление свойств математической модели на основе поведение ( изменения) решения при изменении параметров уравнений и перенос свойств модели на процесс в реакторе.

7. Сопоставление процессов в реакторах различного типа.

8. Выявление особенностей математической модели и, следовательно, особенностей режима.

61. ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС В ХИМИЧЕСКОМ РЕАКТОРЕ. РЕЖИМ ИДЕАЛЬНОГО СМЕШЕНИЯ И ИДЕАЛЬНОГО ВЫТЕСНЕНИЯ. ПРОСТАЯ НЕОБРАТИМАЯ РЕАКЦИЯ А=R.

Математическая модель процессов

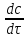=w (c); c = c_{0 при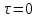} (1)

Где 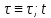в зависимости от процесса

Математическая модель для реакции первого порядка: (т.к. w(c) = -RC): (2)

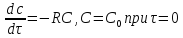(3)

Интегрируя (3) получил:

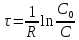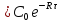и С(4)

Выражая концентрацию через степень превращения [ 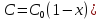, получим из (3):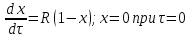(5)

И его решением будет

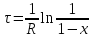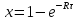и (6)

Графики С (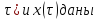на рисунке

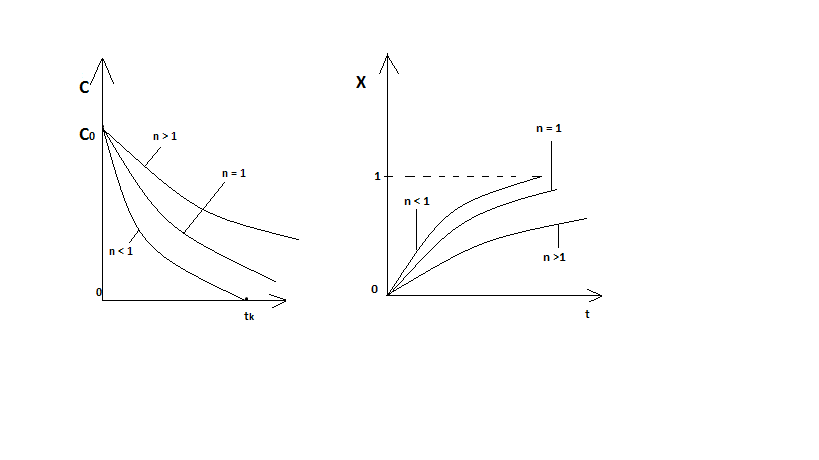
Из графиков видно, что при 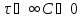или x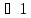 соответственно, следовательно, в необратимой реакции исходное вещество постепенно расходуется до его полного превращения.

Интерпретация решения (4) уравнений математической модели (1) на процессы в режимах ИС - п и ИВ следующая.

В режиме ИС – п процесс не стационарен 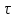≡ t и со временем t концентрация исходного вещества C уменьшается в соответствии с (4).

Но в каждый момент времени – концентрация C во всех точках реактора одинакова.

В режиме ИВ процесс протекает стационарно. Концентрация C меняется по длине 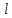реактора.

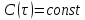То анализ зависимостей С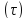(4) или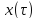(6) показывает влияние условий процесса на изменение концентрацииС, или степени превращения x во времени в режиме ИС – п и распределение C и x по длине реактора в режиме ИВ.