8. 2. Метод вариации произвольных постоянных (метод Лагранжа)

1. Для уравнения (11) составляют соответствующее однородное уравнение (12) и находят его общее решение y_о.о.:

. (14)

2. В уравнении (14) полагают константы функциями от x, т.е. . Эти функции находят из системы:

Решают эту систему методом Крамера. Определитель этой системы – определитель Вронского (он будет отличен от нуля для линейно независимых функций).

.

,...,

Тогда: . Отсюда

.

Подставляя эти значения в (14), получим общее решение уравнения (11):

.

Задача 16. Найти решение задачи Коши

.

Решение. Воспользуемся методом вариации произвольных постоянных. (Следует иметь в виду, что метод имеет место, когда коэффициент при старшей производной равен единице!)

Найдем общее решение уравнения ; т.к. корнями характеристического уравнения являются числа, то.

Предполагая, что с₁ и с₂ – есть функции от x, будем искать решение исходного уравнения в виде , гдеc₁(x) и c₂(x) найдем из системы:

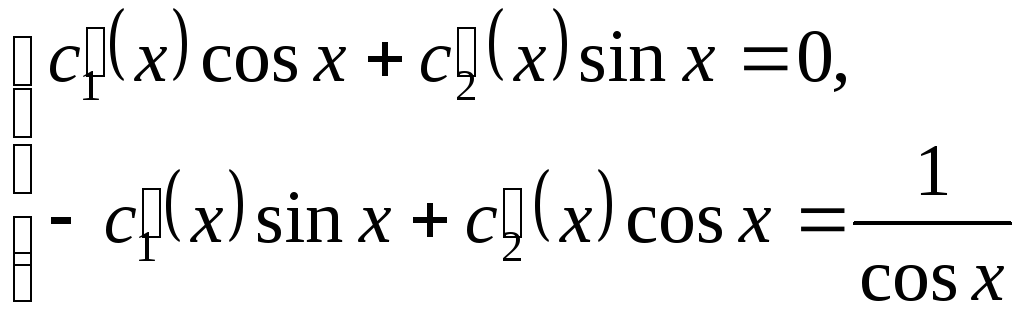
Составим определитель этой системы – определитель Вронского:

.

(Т.к. определитель отличен от нуля, система имеет решение и при том единственное.)

.

Тогда . Отсюда, интегрированием находим

.

Таким образом, общее решение исходного уравнения будет выглядеть так:

.

Для решения задачи Коши найдем :

.

Подставляя начальные условия в инайдем, чтос₁=1, с₂=0. Тогда - частное решение.

9. Литература

Учебники:

1. Шипачев В.С. Высшая математика. – М.: Высшая школа, 1990.

2. Берман А.Ф., Араманович И.Г. Краткий курс математического анализа для ВТУЗов. – М.: Изд. «Наука». Гл.ред. физ.-мат. лит.,1967.

Пособия по решению задач:

1. Данко П.Е., Попов А.Г., Кожевников Т.Е. Высшая математика в упражнениях и задачах: Учеб. пособие для студентов втузов. В 2-х ч. Ч. II. – 4-е изд., испр. и доп./ П.Е. Данко, А.Г. Попов, Т.Е. Кожнвников. – М.: Высшая школа, 1986. – 415 с., ил.

2. Запорожец Г.И. Руководство к решению задач по математическому анализу: Учеб. пособие для студентов втузов. Издание третье, дополненное/ Г.И. Запорожей. – М.: Высшая школа, 1964. – 479 с.

3. Каплан И.А. Практические занятия по высшей математике. В . Ч. 3. Интегральное исчисление функций одной независимой переменной. Интегрирование дифференциальных уравнений./ И.А. Каплан – Харьков: Изд. ХГУ им. М.Горького, 1965. - 374 с.

Методическая литература:

1. Скорик А.И., Шевердинская В.П. Методические указания по выполнению ТР – 2 и контрольной работы «Дифференциальные уравнения». Часть I./ А.И. Скорик. В.П. Шевердинская. – Орел, 1990.– 30 с.

2. Скорик А.И., Шевердинская В.П. Методические указания к выполнению ТР и для индивидуальной работы студентов. Дифференциальные уравнения высших порядков./ А.И. Скорик. В.П. Шевердинская. – Орел, 1992.– 30 с.

Задачники:

1. Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа: Учеб. пособие для втузов./ В.А. Болгов, А.В. Ефимов, А.Ф. Каракулин и др.; под. ред. Ефимова А.В. и Демидовича Б.П. – 2-е изд.– М: Наука. Гл. ред. физ. – мат. лит., 1986.– 368 с.

2. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты): Учеб. пособие для втузов/ Л.А. Кузнецов. – М.: Высшая школа, 1983.– 175 с.

Справочники:

1.Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов.– 13-е изд., исправленное./ И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, Гл. ред. физ. – мат. лит., 1986.– 544 с.

35