1. Уравнения с разделяющимися переменными

Дифференциальные уравнения вида:

(1)

называются уравнениями с разделяющимися переменными. Решая такие уравнения, необходимо преобразовать их так, чтобы одна часть уравнения содержала только переменную у, а другая - толькох, а затем проинтегрировать обе части (поуи похсоответственно).

Например, уравнение (1) надо разделить на , тогда получим. Проинтегрировав обе части, найдем общий интеграл:

. (2)

Кроме найденного общего интеграла (2) уравнению (1) могут также удовлетворять решения, получаемые из уравнения . Если эти решения не входят в общий интеграл (2), то они будут особыми решениями уравнения (1).

Приведем примеры решения конкретного уравнения этого типа.

Задача №1. Найти общий интеграл дифференциального уравнения (ответ представить в виде (х, у)=с).

1.31 .

Решение. Уравнение представлено в дифференциальной форме. Для разделения переменных перенесем все слагаемые в одну часть уравнения и сгруппируем содержащие dxиdy:

Разделим обе части уравнения на , получим.

Почленно интегрируя, получим искомый общий интеграл:

.

В первообразных модули можно опустить, т.к. 1+х²и4+у²величины всегда неотрицательные.

Умножая обе части уравнения на 2 и учитывая свойства логарифма, получим

.

В нашем примере уравнение представлено в дифференциальной форме. Возможны случаи, когда уравнение разрешено относительно производной, т.е. оно имеет вид и, когда не разрешено относительно производной —.

Например, для первого случая . В таких задачах нужно учитывать, что. Тогда,.

Пример ко второму случаю: . Уравнение можно разрешить относительно производной и, таким образом, придем к первому случаю.

2. Однородные уравнения первого порядка

Уравнение первого порядка называется однородным, еслиf(x,y)можно представить как функцию только одного отношения переменных, т.е. уравнение вида. Однородное уравнение приводится к уравнению с разделяющимися переменными посредством замены функцииу(илих) новой функциейtпо формулеy=tx(x=ty), причем.

Дифференциальное уравнение типа:

приводится к однородному с помощью переноса начала координат в точку (х₀,у₀)пересечения прямых, т.е. замена переменныхХ=х-х₀, У=у-у₀.

Если эти прямые не пересекаются, то , и рассматриваемое уравнение сводится к виду, котороеприводится к уравнению с разделяющимися переменными заменой, тогда

Задача №2. Найти общий интеграл дифференциального уравнения

2.31 .

Решение. Данное уравнение первого порядка уже разрешено относительно производной. Установим, что она является функцией только отношения переменных , т.е. установим, что данное уравнение является однородным. Для этого числитель и знаменатель дроби разделим наx². (Другими словами, сократим дробь наx².)

.

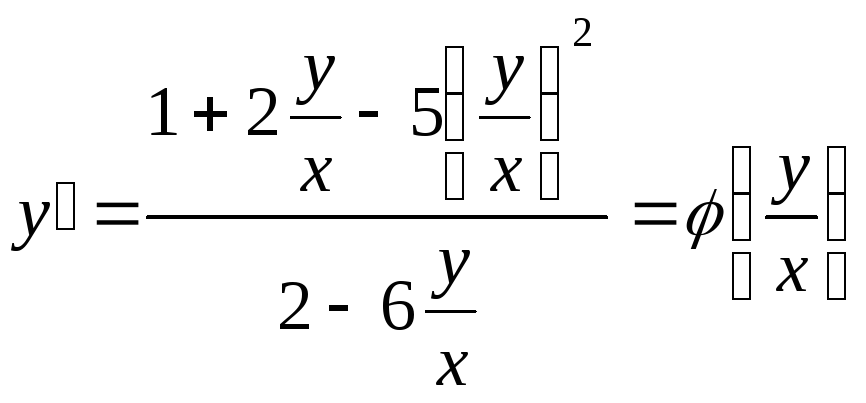Далее вводим новую функцию . Отсюда,. После подстановки данное уравнение преобразуется в уравнение с разделяющимися переменными. Разделим переменные:и, интегрируя, найдем

Возвращаясь к старым переменным, получим

Ответ:

Задача №3. Найти общий интеграл дифференциального уравнения

3.31

Решение. Также как и в задаче №2 это тоже однородное дифференциальное уравнение. Докажем это, найдя точку пересечения прямых, стоящих в числителе и знаменателе и сделав соответствующую замену переменных.

Из последней системы легко видеть, что . Подставим найденныехиув исходное уравнение, получим

.

Далее решаем полученное однородное уравнение путем замены.

Возвращаясь к старым переменным, получим: , что и является ответом.