Основные понятия моделирования систем
Процессы химической технологии — это сложные физико-химические системы, имеющие двойственную детерминированно-стохастическую природу, переменные в пространстве и во времени. Участвующие в них потоки вещества, как правило, многофазные и многокомпонентные. В ходе протекания процесса в каждой точке фазы и на границах раздела происходит перенос импульса, энергии, массы. Весь процесс в целом протекает в аппарате с конкретными геометрическими характеристиками, оказывающими, в свою очередь, влияние на характер этого процесса.
Под математическим моделированием понимают изучение свойств объекта на математической модели. Его целью является определение оптимальных условий протекания процесса, управление им на основе математической модели и перенос результатов на объект.
Основным понятием метода математического моделирования является понятие математической модели. Математической моделью называется приближенное описание какого-либо явления или процесса внешнего мира, выраженное с помощью математической символики.
Математическое моделирование включает три взаимосвязанных этапа: 1) составление математического описания изучаемого объекта; 2) выбор метода решения системы уравнений математического описания и реализация его в форме моделирующей программы; 3) установление соответствия (адекватности) модели объекту.
На этапе составления математического описания предварительно выделяют основные явления и элементы в объекте и затем устанавливают связи между ними. Далее, для каждого выделенного элемента и явления записывают уравнение (или систему уравнений), отражающее его функционирование. Кроме того, в математическое описание включают уравнения связи между различными выделенными явлениями. В зависимости от процесса математическое описание может быть представлено в виде системы алгебраических, дифференциальных, интегральных и интегро-дифференциальных уравнений.
Этап выбора метода решения и разработки моделирующей программы подразумевает выбор наиболее эффективного метода решения из имеющихся (под эффективностью имеются в виду быстрота получения и точность решения) и реализацию его сначала в форме алгоритма решения, а затем — в форме программы, пригодной для расчета на ЭВМ.
Построенная на основе физических представлений модель должна верно качественно и количественно описывать свойства моделируемого процесса, т.е. она должна быть адекватна моделируемому процессу. Для проверки адекватности математической модели реальному процессу нужно сравнить результаты измерений на объекте в ходе процесса с результатами предсказания модели в идентичных условиях.
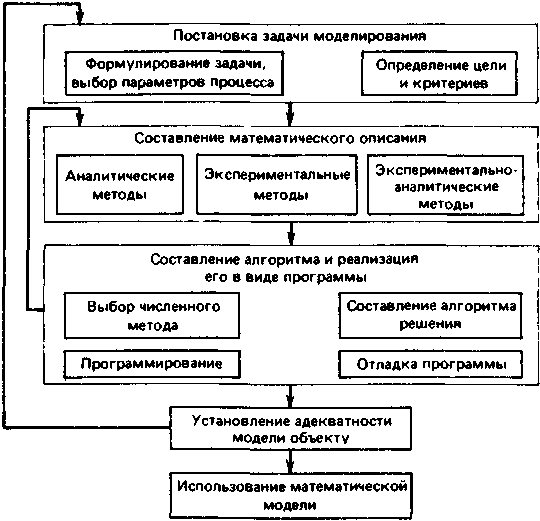
Рис. 1. Этапы разработки математической модели
В зависимости от степени полноты математического описания можно выделить два предельных случая: а) известны полная система уравнений, описывающая все основные стороны моделируемого процесса, и все числовые значения параметров этих уравнений; б) полное математическое описание процесса отсутствует. Этот второй случай типичен для решения кибернетических задач, в которых приходится иметь дело с управлением процессами при наличии неполной информации об объекте и действующих на него возмущениях. При отсутствии достаточной информации об исследуемых явлениях их изучение начинается с построения простейших моделей, но без нарушения основной (качественной) специфики исследуемого процесса.
Аналитическое моделирование – это моделирование при котором функционирование элементов системы записано в виде функциональных соотношений или логических условий.
Эта модель исследуется следующими методами:
аналитически, когда стремятся получить явные зависимости искомых характеристик.
численно, когда нельзя решить уравнения аналитически, и получают числовые результаты решения при конкретных начальных данных.
качественно, когда нет решения в явном виде, но можно найти некоторые свойства решения (например устойчивость).
Имитационное моделирование – это моделирование при котором воспроизводится процесс функционирования системы во времени, с сохранением логической структуры и с последовательности протекания во времени, что дает возможность оценить характеристики системы.