Контрольная работа для студентов заочного отделения,

группы 1320,1321,1322.

(2013/2014 уч.год, второй семестр)

Преподаватель: к.п.н, доцент Т.Г. Макусева

Задача 1. Изменить порядок интегрирования. Сделать чертеж области интегрирования.

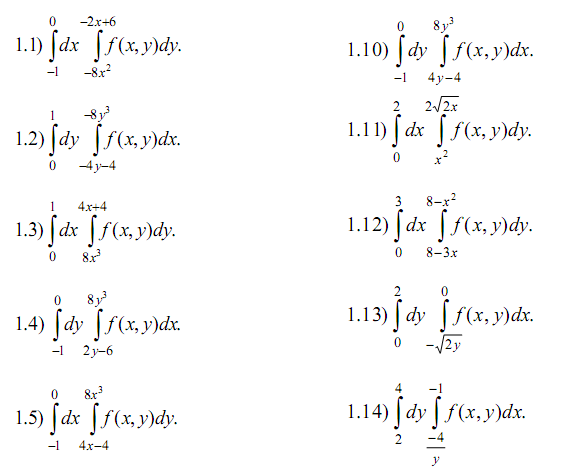
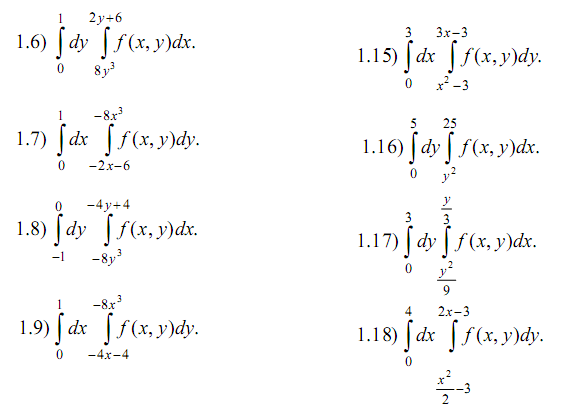
Задача 2. Вычислить определенный интеграл (Номер задания соответствует последней цифре Вашей зачетной книжки).

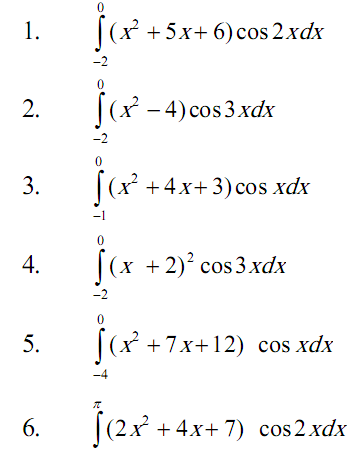
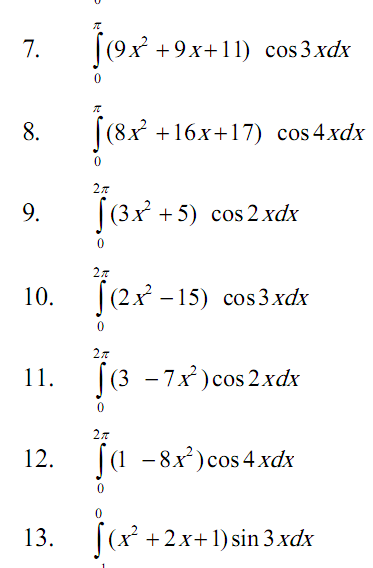
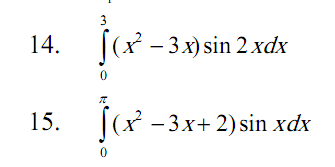
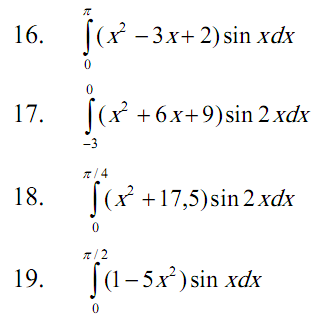
Задача 3. Комплексные числа.

Вариант №1

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

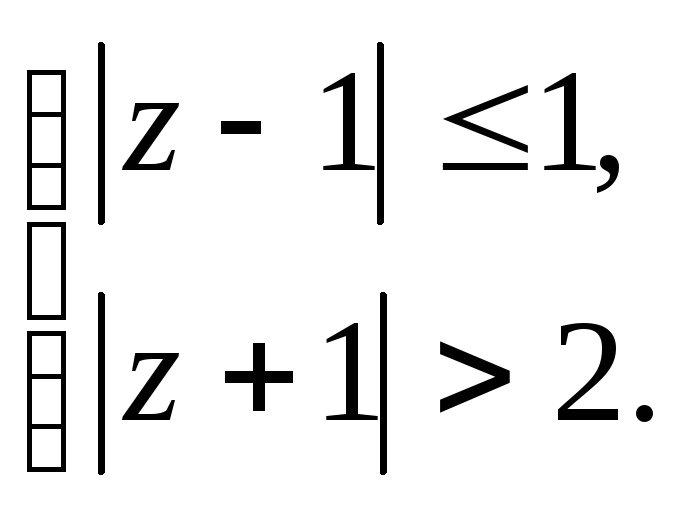Вариант №2

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

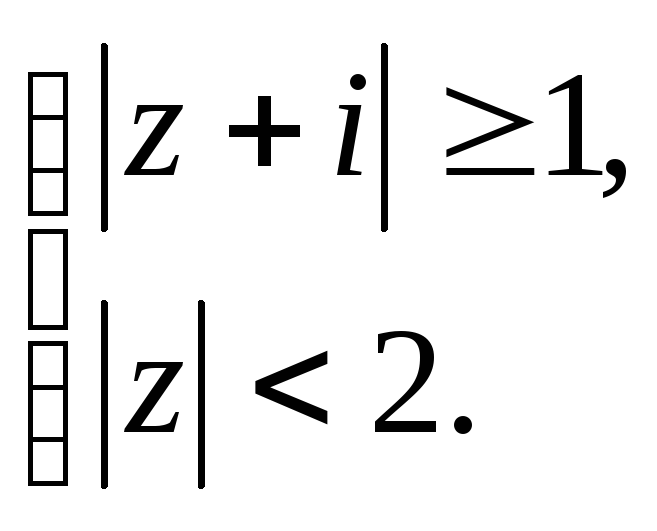Вариант №3

Задание 1.

а) Найти модуль и аргумент чисел = и = Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

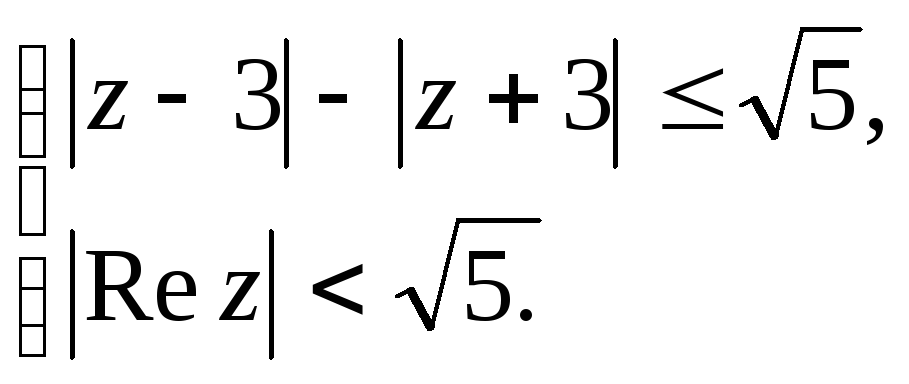Вариант №4

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

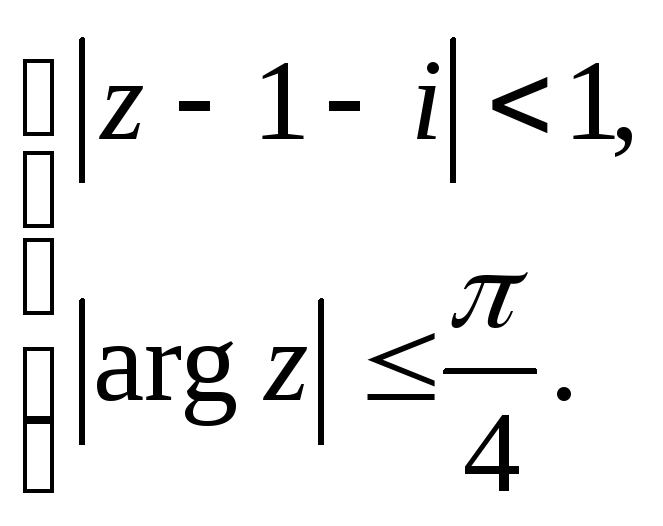Вариант №5

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

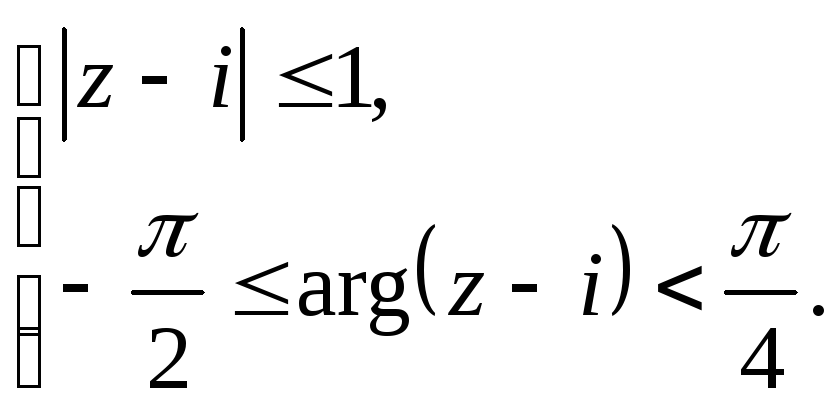Вариант №6

Задание 1.

а) Найти модуль и аргумент чисел = и Изобразить числа на комплексной плоскости. Представить числа в тригон=. ометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

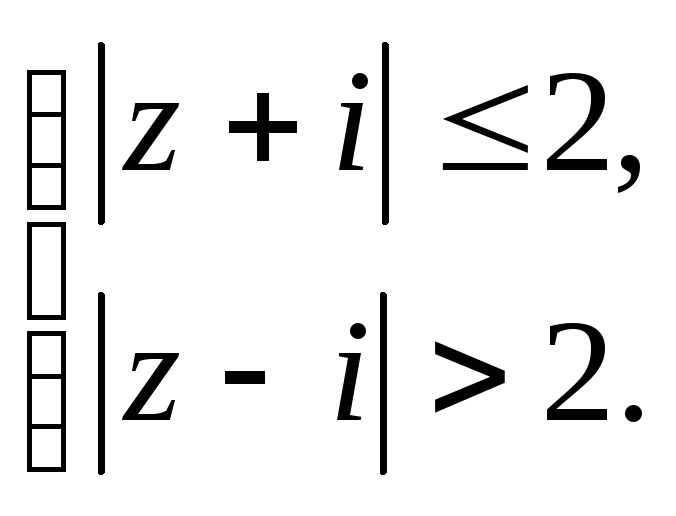Вариант №7

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а)

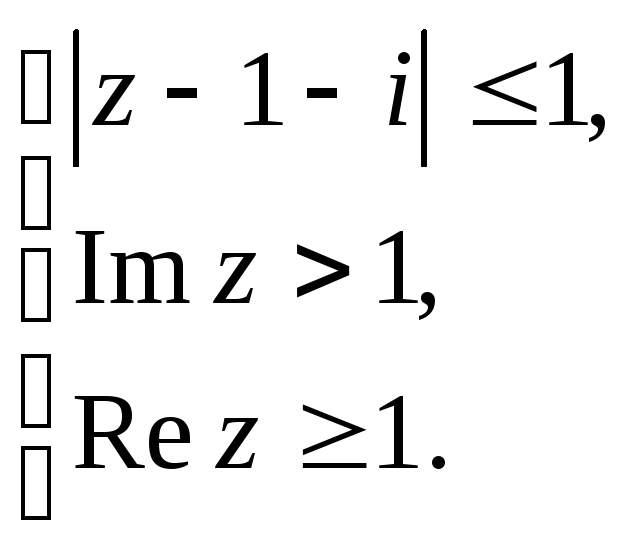
Вариант №8

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а)

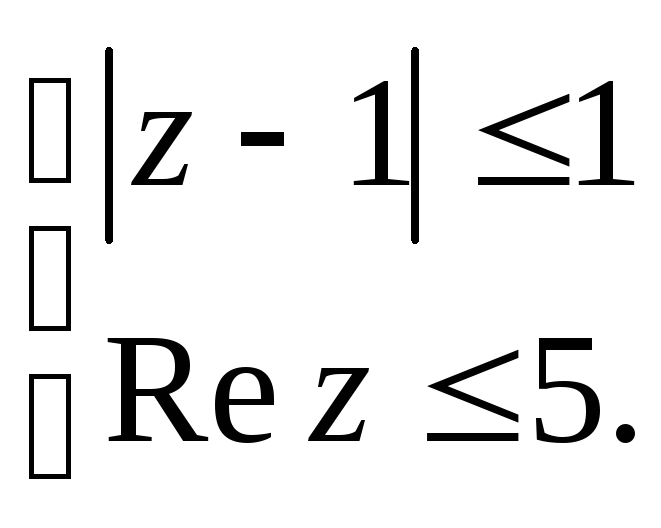
Вариант №9

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а)

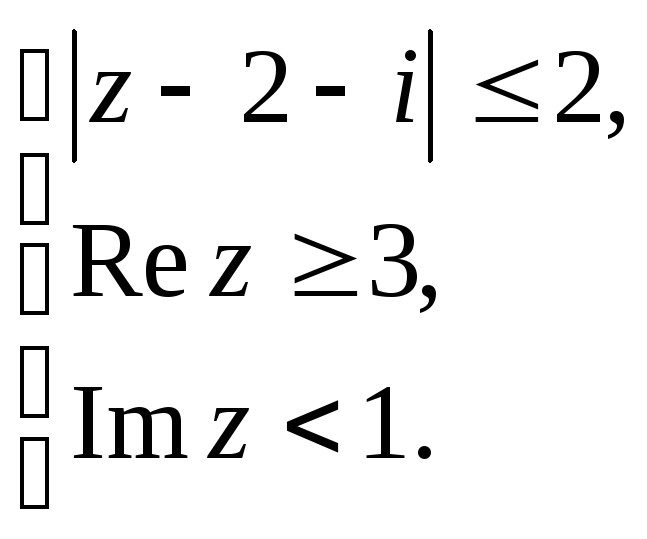
Вариант №10

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

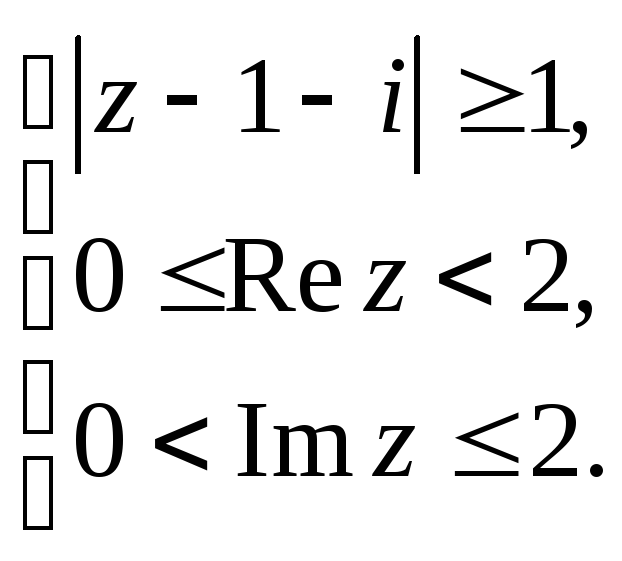Вариант №11

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

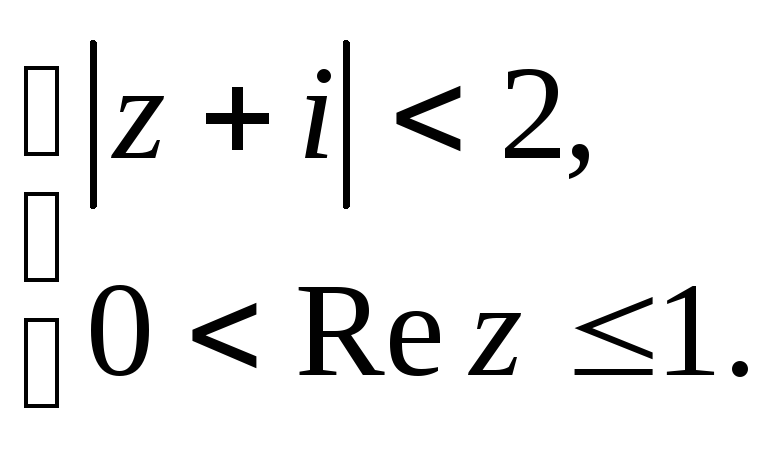Вариант №12

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

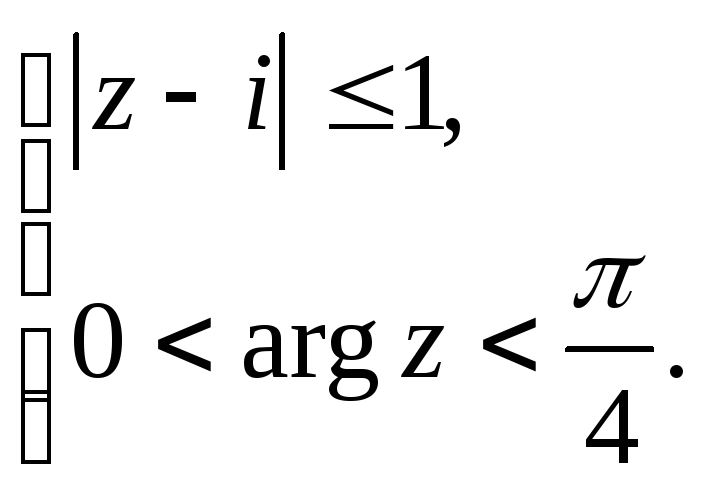Вариант №13

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

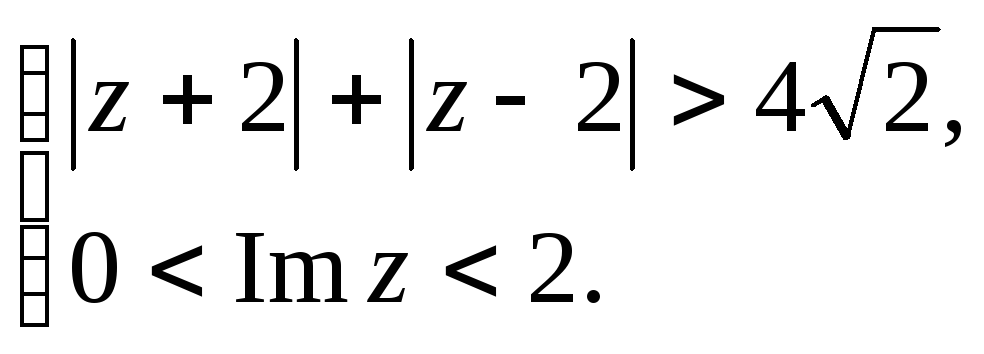Вариант №14

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

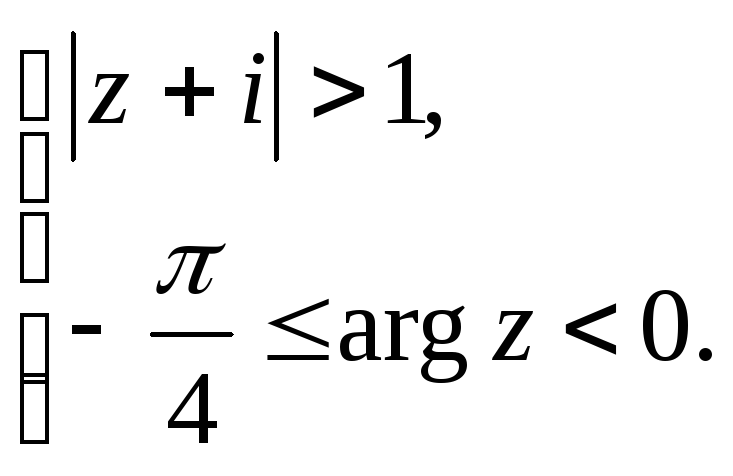Вариант №15

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

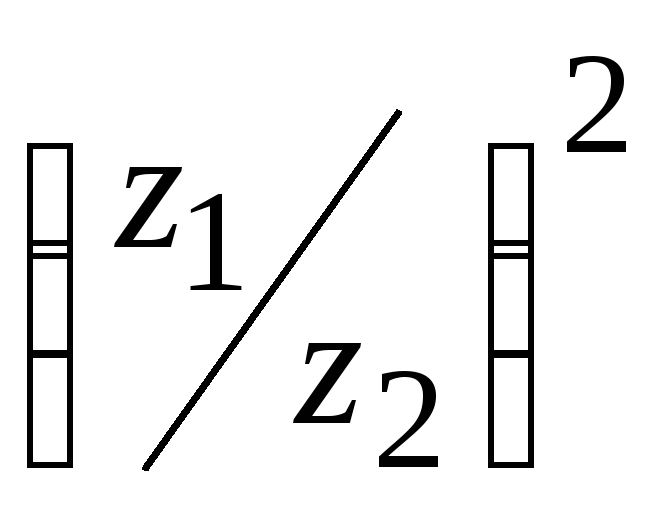Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

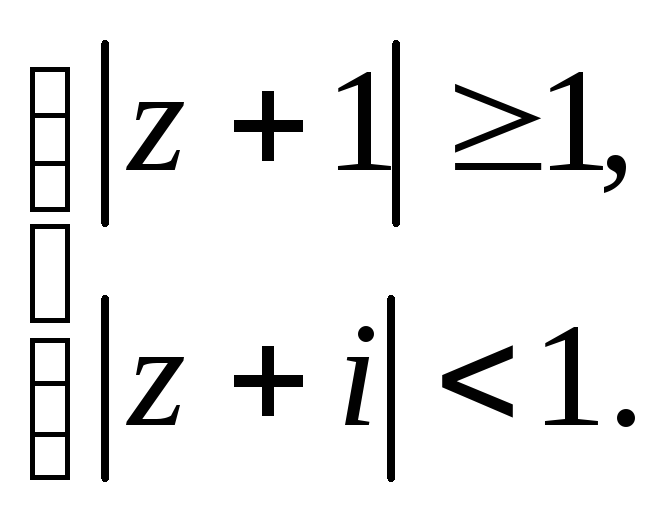Вариант №16

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а)

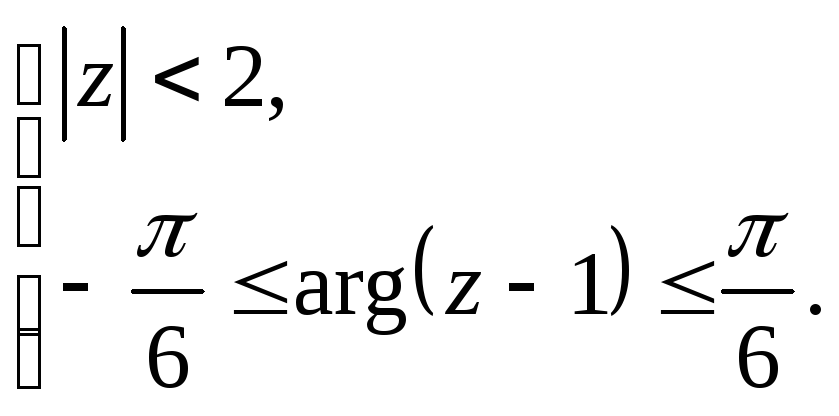
Вариант №17

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

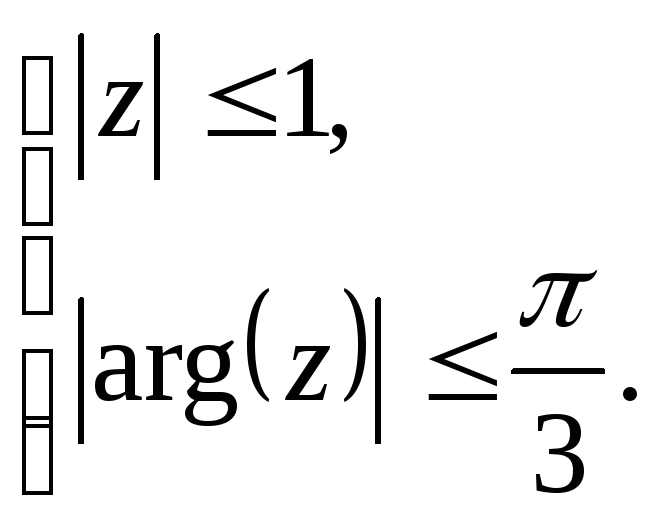Вариант №18

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

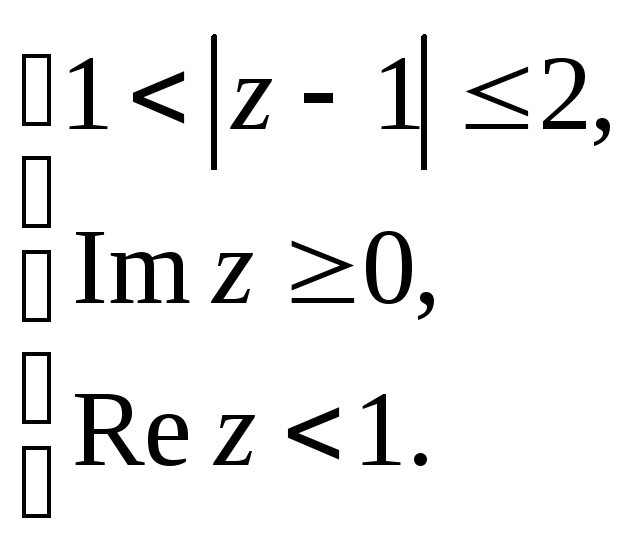Вариант №19

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

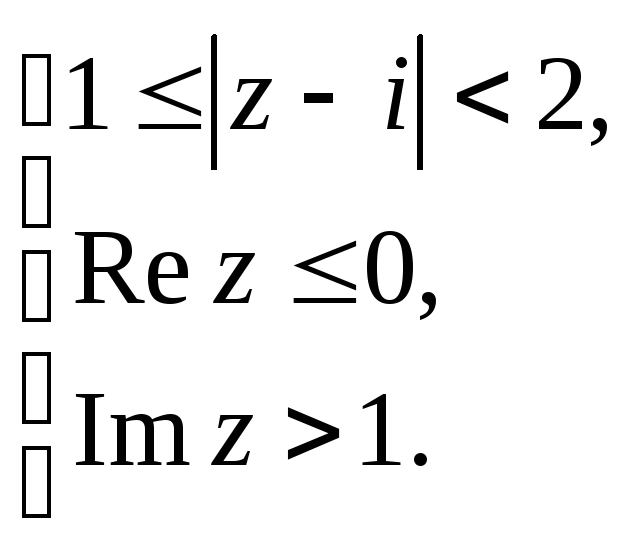Вариант №20

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

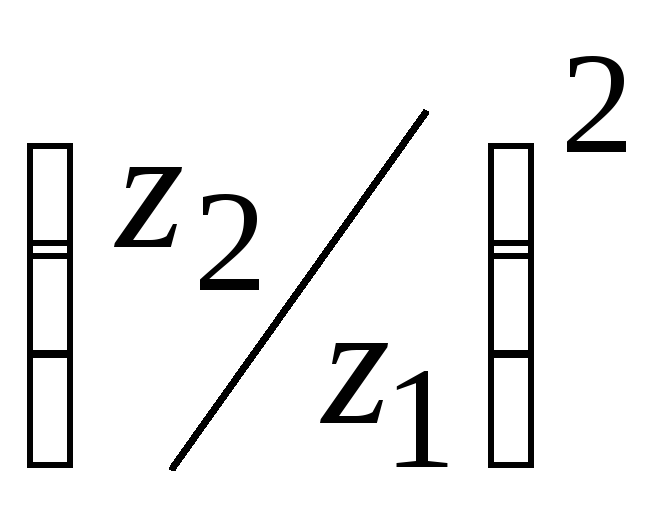Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

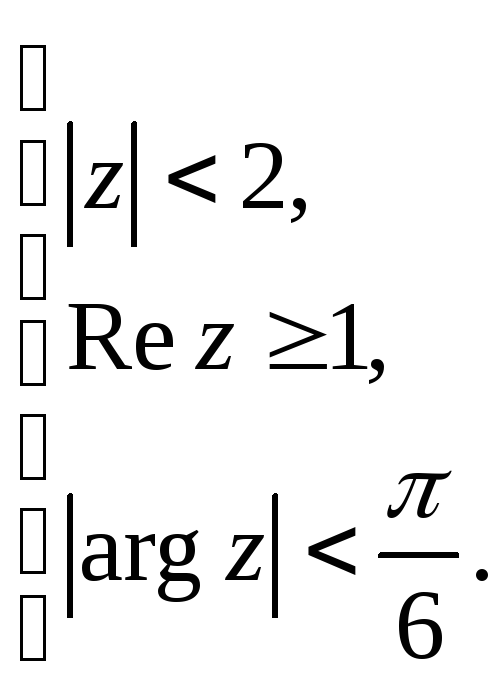Вариант №21

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

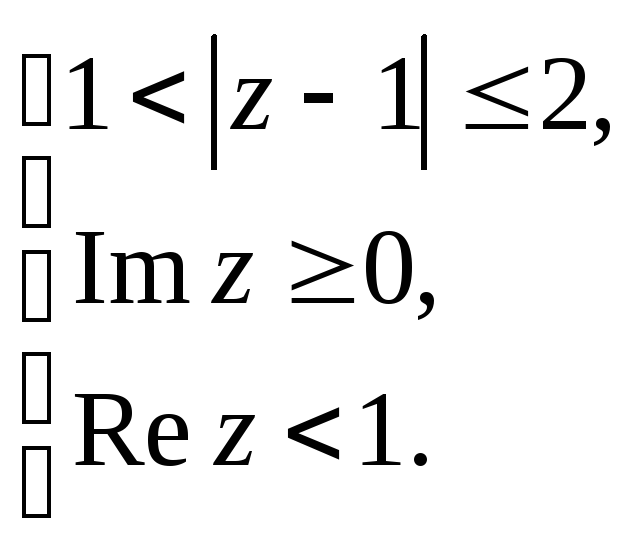Вариант №22

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

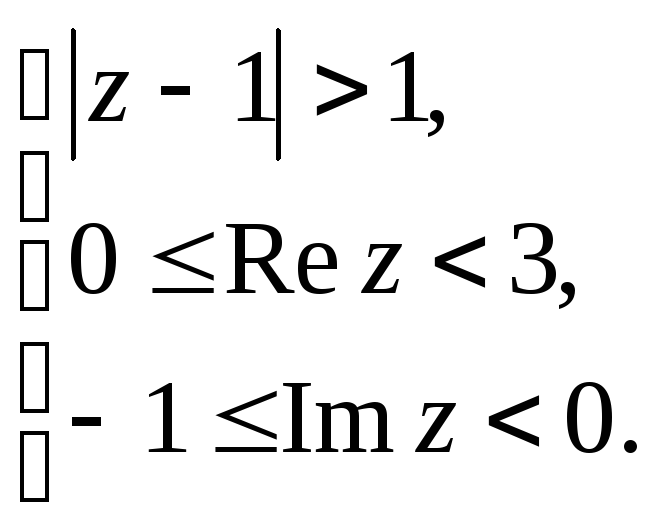Вариант №23

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а)

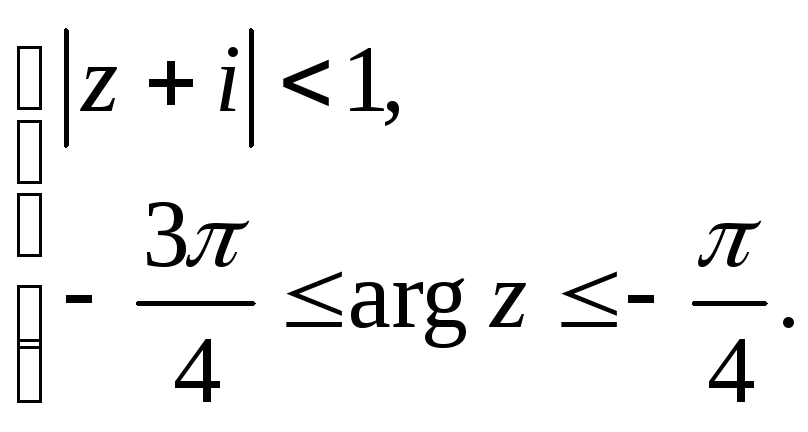
Вариант №24

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а) ;

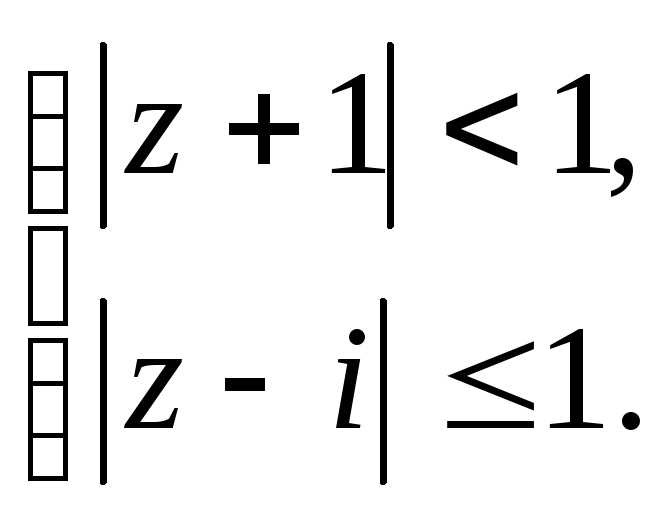Вариант №25

Задание 1.

а) Найти модуль и аргумент чисел = и =. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: , .

Задание 5. Построить область плоскости , определяемую данными неравенствами.

а)

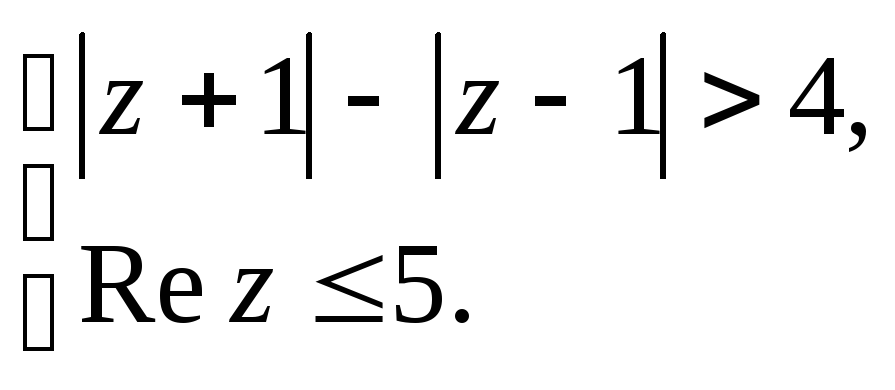
Задача 4. Вычислить площадь плоской фигуры с помощью определенного интеграла. Сделать рисунок.

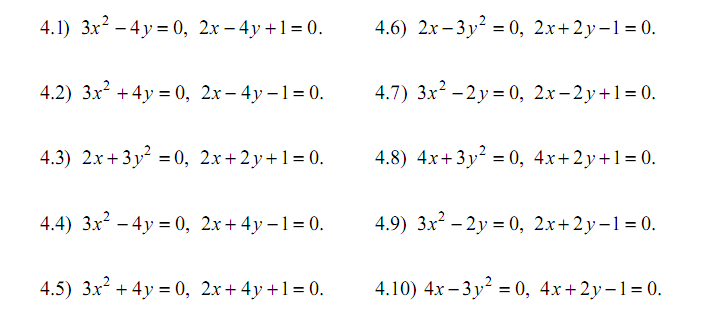
Задача 5.

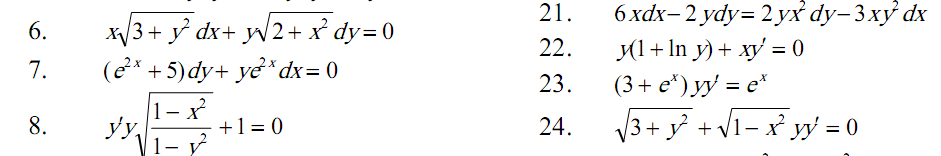
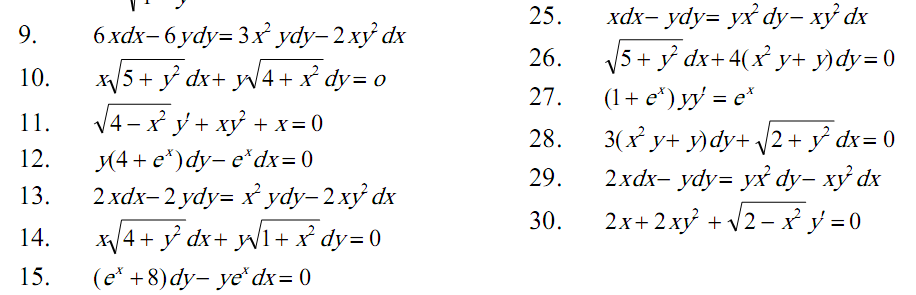
Задача 6.

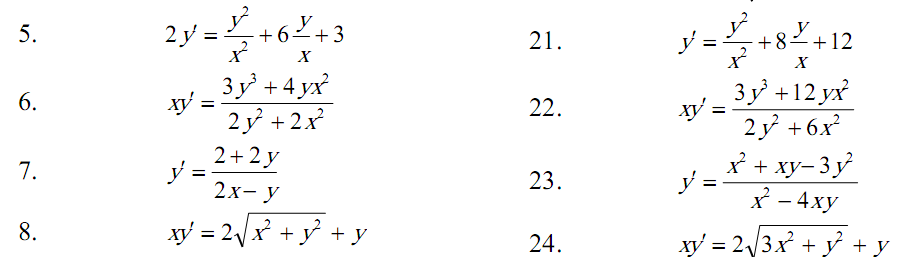
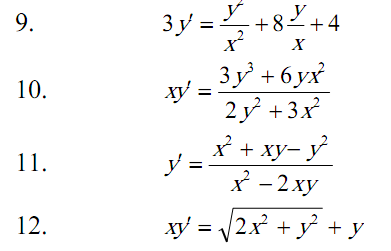
Примеры решения задач.

Задача 2. Вычислить определенный интеграл.

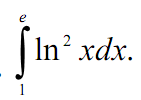
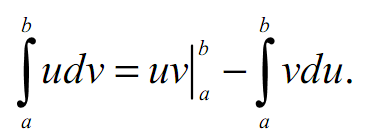
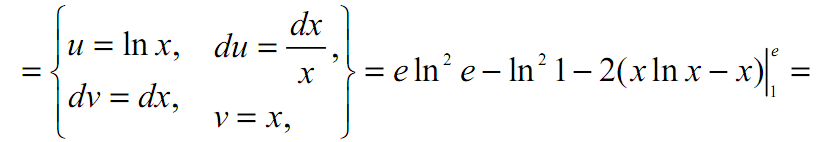
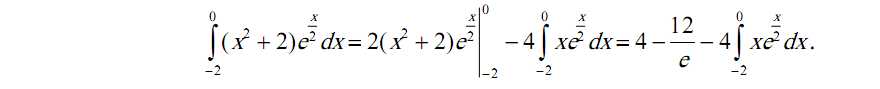
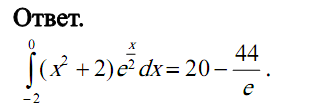
Задача 4. 1) Вычислить площадь фигуры, ограниченной линиями , (рис. 8).

Решение. Площадь фигуры, ограниченной сверху и снизу непрерывными линиями и , пересекающимися в точках с абсциссами и , определяется по формуле

. (1)

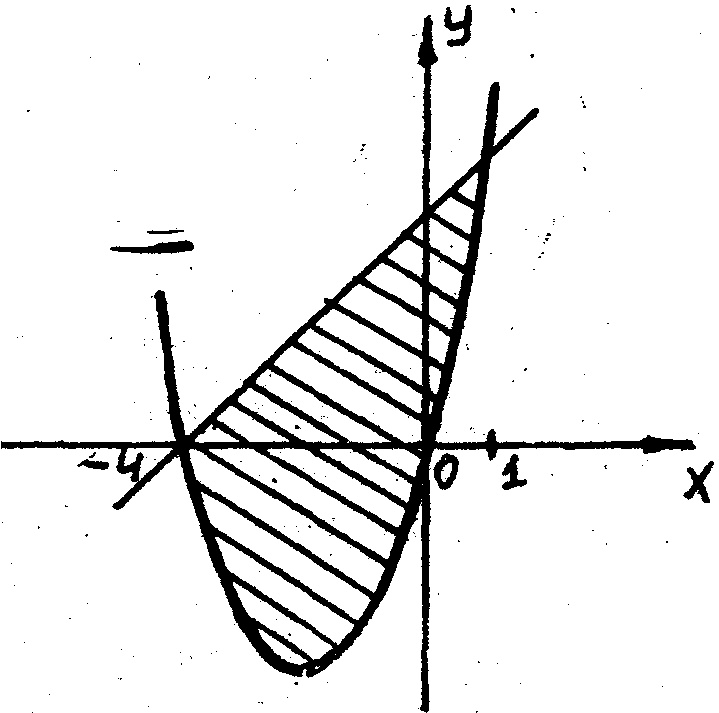Для нахождения точек пересечения данных линий решаем систему уравнений

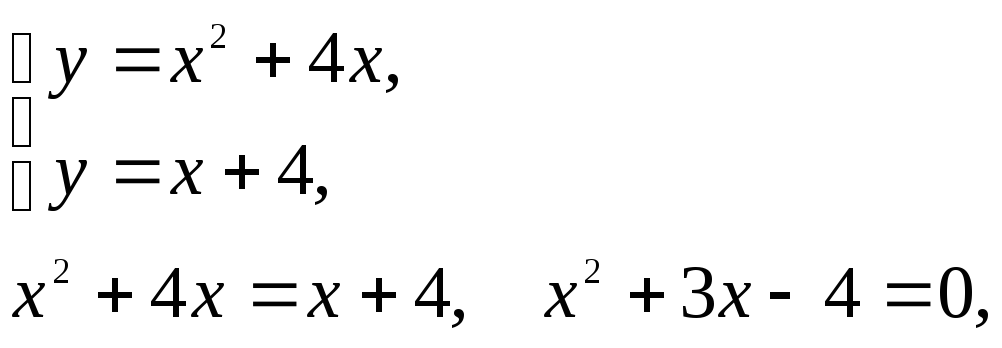
откуда . Применяя формулу (1), получим:

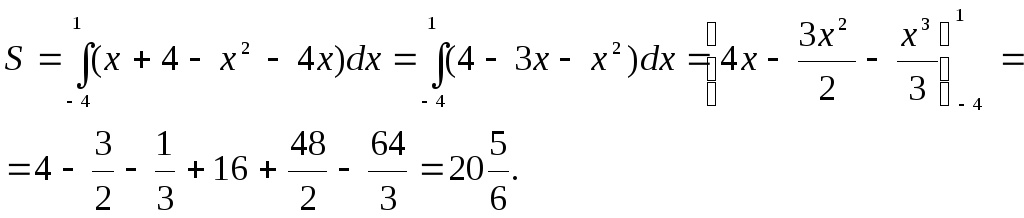
Задача 5.

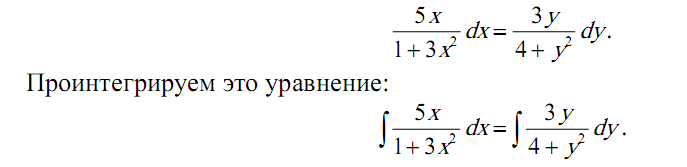
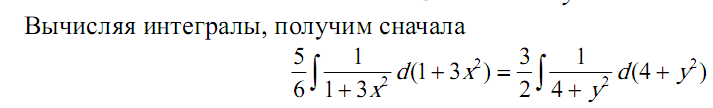
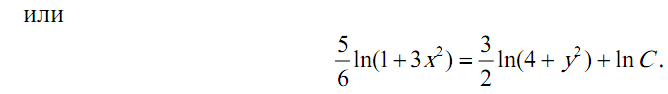
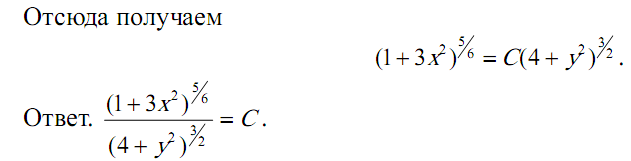
Задача 6.