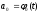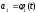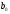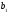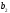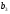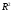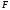3.3. Второй этап решения математической задачи
3.3.1. Формулировка математической задачи
Известны
,
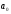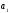– параметры функции
,
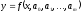зависимые переменные от времени
длительности нарушения гемодинамики
мозга, т.е.
,
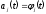где
.
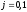Нужно подобрать вид функции, характеризующий энергетическое состояние мозга при ишемии разной продолжительности.
Для интактных животных зависимость
функции принимает вид
,
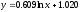поскольку функция не зависит от времени.
В случае ишемии различной продолжительности
при условии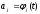
зависимость приведена в таблице 15.
Табл. 15. Зависимость
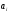от времени ишемии.
|
t, ч |
|
|
|
0.5 |
0.573 |
1.116 |
|
18 |
0.382 |
0.887 |
|
72 |
0.536 |
0.975 |
|
168 |
0.701 |
1.148 |
|
720 |
0.497 |
0.912 |
3.3.2. Геометрическая интерпретация зависимостей
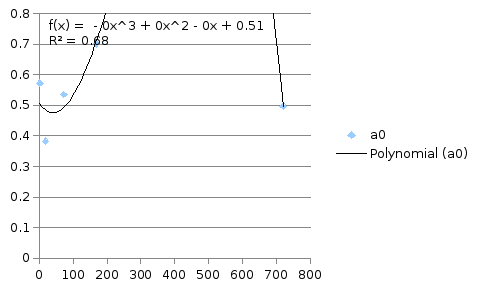
Рис. 7. Зависимость
.
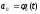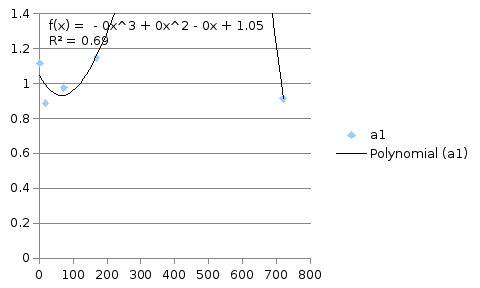
Рис. 8. Зависимость
.
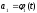3.3.3. Решение задачи
Задана элементарная функция вида
.
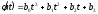Для решения задачи используем метод наименьших квадратов.
,
.
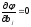Таким образом, выражение принимает вид:
.
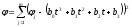Записываем необходимые условия экстремума:
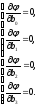
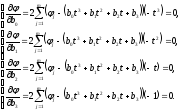
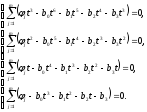
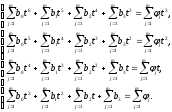
Далее решаем систему уравнений методом Крамера:
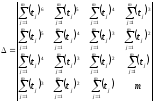
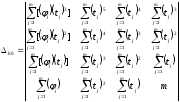
3.3.4. Результаты определения параметров функции
В результате проведенных исследований получаем функцию двух переменных
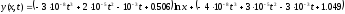
Табл. 16. Параметры функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
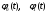
0.506 |
0.682 |
6.434 |
10.13 |
|
|
|
|
|
1.049 |
0.687 |
6.585 |
10.13 |
Коэффициент детерминации
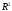стремится к единице слабо. Тот факт, что
,
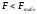это подтверждает. Следовательно,
кубический многочлен подходит для
аппроксимации данных функций не лучшим
образом. Но так как строилась приближенная
модель, и коэффициент детерминации
определяет связь в пределах «значительной»,
то данный результат можно считать
удовлетворительным для описания ишемии
на некоторых сроках.
3.4. Проверка прогностической способности модели
3.4.1. Табулирование функции
В результате табулирования с шагом полчаса получилось 1500 значений. Рассмотрим значения вблизи экспериментальных данных. Полная таблица табулирования представлена а приложении.
Табл. 17. Выборочные результаты табулирования вблизи экспериментальных данных
|
t |
x |
y |
|
0,5 |
0,372 |
0,547633 |
|
1 |
0,37225 |
0,546974 |
|
1,5 |
0,3725 |
0,54632 |
|
2 |
0,37275 |
0,54567 |
|
2,5 |
0,373 |
0,545024 |
|
3 |
0,37325 |
0,544382 |
|
3,5 |
0,3735 |
0,543745 |
|
4 |
0,37375 |
0,543112 |
|
4,5 |
0,374 |
0,542483 |
|
5 |
0,37425 |
0,541859 |
|
5,5 |
0,3745 |
0,541239 |
|
6 |
0,37475 |
0,540623 |
|
6,5 |
0,375 |
0,540012 |
|
7 |
0,37525 |
0,539405 |
|
7,5 |
0,3755 |
0,538802 |
|
8 |
0,37575 |
0,538204 |
|
8,5 |
0,376 |
0,53761 |
|
9 |
0,37625 |
0,53702 |
|
9,5 |
0,3765 |
0,536435 |
|
10 |
0,37675 |
0,535855 |
|
10,5 |
0,377 |
0,535279 |
|
11 |
0,37725 |
0,534707 |
|
11,5 |
0,3775 |
0,53414 |
|
12 |
0,37775 |
0,533577 |
|
12,5 |
0,378 |
0,533019 |
|
13 |
0,37825 |
0,532466 |
|
13,5 |
0,3785 |
0,531916 |
|
14 |
0,37875 |
0,531372 |
|
14,5 |
0,379 |
0,530832 |
|
15 |
0,37925 |
0,530296 |
|
15,5 |
0,3795 |
0,529765 |
|
16 |
0,37975 |
0,529239 |
|
16,5 |
0,38 |
0,528717 |
|
17 |
0,38025 |
0,5282 |
|
17,5 |
0,3805 |
0,527688 |
|
18 |
0,38075 |
0,52718 |
|
18,5 |
0,381 |
0,526676 |
|
19 |
0,38125 |
0,526178 |
|
20 |
0,38175 |
0,525194 |
|
21 |
0,38225 |
0,52423 |
|
22 |
0,38275 |
0,523284 |
|
32 |
0,38775 |
0,514873 |
|
42 |
0,39275 |
0,508416 |
|
52 |
0,39775 |
0,50397 |
|
62 |
0,40275 |
0,501581 |
|
68 |
0,40575 |
0,501149 |
|
68,5 |
0,406 |
0,501147 |
|
69 |
0,40625 |
0,501151 |
|
69,5 |
0,4065 |
0,501159 |
|
70 |
0,40675 |
0,501173 |
|
70,5 |
0,407 |
0,501193 |
|
71 |
0,40725 |
0,501217 |
|
71,5 |
0,4075 |
0,501247 |
|
72 |
0,40775 |
0,501282 |
|
72,5 |
0,408 |
0,501322 |
|
73 |
0,40825 |
0,501368 |
|
73,5 |
0,4085 |
0,501419 |
|
74 |
0,40875 |
0,501475 |
|
74,5 |
0,409 |
0,501537 |
|
75 |
0,40925 |
0,501604 |
|
75,5 |
0,4095 |
0,501676 |
|
76 |
0,40975 |
0,501753 |
|
76,5 |
0,41 |
0,501836 |
|
77 |
0,41025 |
0,501924 |
|
77,5 |
0,4105 |
0,502017 |
|
78 |
0,41075 |
0,502116 |
|
78,5 |
0,411 |
0,50222 |
|
79 |
0,41125 |
0,502329 |
|
79,5 |
0,4115 |
0,502444 |
|
80 |
0,41175 |
0,502564 |
|
80,5 |
0,412 |
0,502689 |
|
81 |
0,41225 |
0,502819 |
|
81,5 |
0,4125 |
0,502955 |
|
82 |
0,41275 |
0,503096 |
|
162 |
0,45275 |
0,592814 |
|
162,5 |
0,453 |
0,593776 |
|
163 |
0,45325 |
0,594742 |
|
163,5 |
0,4535 |
0,595713 |
|
164 |
0,45375 |
0,596689 |
|
164,5 |
0,454 |
0,597669 |
|
165 |
0,45425 |
0,598653 |
|
165,5 |
0,4545 |
0,599643 |
|
166 |
0,45475 |
0,600636 |
|
166,5 |
0,455 |
0,601635 |
|
167 |
0,45525 |
0,602638 |
|
167,5 |
0,4555 |
0,603645 |
|
168 |
0,45575 |
0,604657 |
|
168,5 |
0,456 |
0,605673 |
|
169 |
0,45625 |
0,606694 |
|
169,5 |
0,4565 |
0,60772 |
|
170 |
0,45675 |
0,60875 |
|
170,5 |
0,457 |
0,609784 |
|
171 |
0,45725 |
0,610823 |
|
171,5 |
0,4575 |
0,611866 |
|
172 |
0,45775 |
0,612914 |
|
172,5 |
0,458 |
0,613967 |
|
173 |
0,45825 |
0,615023 |
|
173,5 |
0,4585 |
0,616084 |
|
174 |
0,45875 |
0,61715 |
|
715 |
0,72925 |
-0,08025 |
|
715,5 |
0,7295 |
-0,0884 |
|
716 |
0,72975 |
-0,09659 |
|
716,5 |
0,73 |
-0,1048 |
|
717 |
0,73025 |
-0,11303 |
|
717,5 |
0,7305 |
-0,1213 |
|
718 |
0,73075 |
-0,12959 |
|
718,5 |
0,731 |
-0,13791 |
|
719 |
0,73125 |
-0,14626 |
|
719,5 |
0,7315 |
-0,15463 |
|
720 |
0,73175 |
-0,16304 |
|
720,5 |
0,732 |
-0,17147 |
|
721 |
0,73225 |
-0,17992 |
|
721,5 |
0,7325 |
-0,18841 |
|
722 |
0,73275 |
-0,19692 |
|
722,5 |
0,733 |
-0,20546 |
|
723 |
0,73325 |
-0,21403 |
|
723,5 |
0,7335 |
-0,22263 |
|
724 |
0,73375 |
-0,23125 |
|
724,5 |
0,734 |
-0,2399 |
|
725 |
0,73425 |
-0,24858 |
Как видно из табл. 17, данная функция подходит для ишемии на малых сроках, продолжительностью в несколько часов или дней, но совершенно неприменима для ишемии более 230 часов.