
- •3. Принцип плотнейшей упаковки. Одномерная и двумерная упаковки одинаковых шаров
- •4. Двухслойная и трехслойная упаковки одинаковых шаров в пространстве
- •5. Симметрия двухслойной и трехслойной плотнейших упаковок одинаковых шаров
- •6. Координаты шаров и пустот в двухслойной и трехслойной упаковках
- •7. Многослойные плотнейнше упаковки одинаковых шаров
6. Координаты шаров и пустот в двухслойной и трехслойной упаковках
Зная число твердых шаров, октаэдрических и тетраэдрических пустот в плонейших упаковках и считая, что все шары, октаэдрические и тетраэдрические пустоты взаимно эквивалентны, можно найти правильные системы точек пространственных групп, по которым они располагаются. Центры шаров, октаэдрических и тетраэдрических пустот будут иметь координаты, совпадающие с координатами точек соотвествующих правильных систем.
Наше рассмотрение начнем с трехслойной упаковки. Найдем число шаров, приходящихся на элементарную ячейку кубической упаковки. Из рис. 12 видно, что по положению в элементарной ячейке все шары можно условно разделить на два типа — находящиеся в вершинах элементарного куба и в серединах граней. Каждый шар, находящийся в вершине элементарной ячейки, принадлежит одновременно восьми элементарным ячейкам. С учетом того, что таких шаров восемь, получаем, что они дают в среднем один шар на элементарную ячейку. Шаров, находящихся в серединах граней, — шесть, и каждый принадлежит одновременно двум элементарным ячейкам. Они дают три шара на ячейку. Таким образом, одной элементарной ячейке трехслойной упаковки принадлежат четыре шара.
Выше в §4 мы рассчитали, что на один шар плотнейших упаковок приходится одна октаэдрическая и две тетраэдрические пустоты. Следовательно, в кубической элементарной ячейке содержится четыре октаэдрические и восемь тетраэдрических пустот.
Итак, мы должны разместить четыре шара, четыре октаэдрические и восемь тетраэдрических пустот в элементарной ячейке кристалла, структура которого описывается пространственной группой Fm3m. Эта группа имеет две четырехкратные 4(a), 4(b) и одну восьмикратную 8(c) правильные системы точек. Симметрия позиций 4(a) и 4(b) — m3m, позиции 8(c) — 43m. Это значит, что координаты этих правильных систем точек описывают центры шаров, центры октаэдров и центры тетраэдров (точки, в которых пересекаются все элементы симметрии точечных групп шаров, октаэдров и тетраэдров) соответственно. Таким образом, при совмещении начала координат с центром шара шары и пустоты в кубической плотнейшей упаковке имеют следующие координаты (в долях ребер элементарной ячейки):

Для подсчета числа шаров и пустот, приходящихся на одну элементарную ячейку выберем начало координат в центре одного из шаров. Тогда элементарная ячейка будет представлять собой параллелепипед, в основании которого лежит ромб и в вершинах которого располагаются центры шаров (рис.14). Из рисунка видно, что, как и в трехслойной упаковке, в элементарной ячейке гексагональной плотнейшей упаковки присутствуют шары двух типов. Шары в вершинах элементарного параллелепипеда принадлежат одновременно восьми элементарным ячейкам. Следовательно, восемь вершин параллелепипеда дают один шар на элементарную ячейку. Кроме того, в элементарной ячейке имеется еще один шар, который не располагается на какой-либо грани или на ребре ячейки, т. е. его центр лежит внутри элементарного параллелепипеда. Он дает еще один шар на ячейку. Таким образом, в элементарной ячейке двухслойной плотнейшей упаковки содержатсядва шара. С учетом числа пустот, приходящихся на один шар, получаем, что в элементарной ячейке ГПУ-упаковки имеются две октаэдрические и четыре тетраэдрические пустоты.

Рис.14. Элементарная ячейка двухслойной плотнейшей упаковки:
Изображен ромб — основание гексагональной элементарной ячейки — и шар, расположенный внутри элементарной ячейки. Начало координат выбрано в центре шара
Таким
образом, мы должны в кристаллическом
пространстве с симметрией Р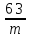 mc
расположить шары и пустоты по правильным
системам точек с кратностью 2 и 4. Обратимся
к списку правильных систем точек группы
Р
mc
расположить шары и пустоты по правильным
системам точек с кратностью 2 и 4. Обратимся
к списку правильных систем точек группы
Р mc.
Кратность обшей правильной системы
точек равна 24. Следовательно, как и в
трехслойной упаковке, шары и пустоты
располагаются по частным правильным
системам точек.
mc.
Кратность обшей правильной системы
точек равна 24. Следовательно, как и в
трехслойной упаковке, шары и пустоты
располагаются по частным правильным
системам точек.
Для
группы Р mc
характерны четыре двухкратные и две
четырехкратные правильные системы
точек:
mc
характерны четыре двухкратные и две
четырехкратные правильные системы
точек:

 mc
и соответственно координаты точек
правильной системы записаны, исходя из
того, что начало кристаллографической
системы координат выбрано в центре
инверсии на винтовой оси 6-го порядка
63, т. е. не в центре шара, как это показано
на рис. 14, а в центре октаэдрической
пустоты (рис. 15).
mc
и соответственно координаты точек
правильной системы записаны, исходя из
того, что начало кристаллографической
системы координат выбрано в центре
инверсии на винтовой оси 6-го порядка
63, т. е. не в центре шара, как это показано
на рис. 14, а в центре октаэдрической
пустоты (рис. 15).
Видно, что ненулевые значения координат X и Y характерны лишь для двухкратных правильных систем точек d или с. Поэтомудля описания координат шаров могут быть использованы только эти правильные системы точек.

Рис.15. Элементарная ячейка двухслойной плотнейшей упаковки при стандартном выборе кристаллографической системы координат:
Начало системы координат выбрано на оси 63 в центре октаэдрической пустоты (в центре инверсии)
Правильные
системы точек d
и с
отличаются друг от друга лишь тем, что
все их точки смещены по оси Z
на половину трансляции. Примем за
координаты центров шаров в двухслойной
упаковке координаты точек правильной
системы d.
Для октаэдрических пустот выбираем
двухкратную правильную систему точек
а.
Это связано с тем, что группа собственной
симметрии октаэдра Oh
должна включать в себя группу симметрии
частной позиции. В группе Р mc
имеются две двухкратные правильные
системы точек с нулевыми координатами
X
и Y:
а
и b.
Им соответствуют точечные группы
симметрии позиций Зm
= D3d
и
6m2
= D3h.
Октаэдр может размещаться лишь в той
позиции, группа точечной симметрии
которой является подгруппой Оh
— группы симметрии октаэдра. Это
означает, что в качестве координат
центров октаэдрических пустот мы должны
выбрать координаты точек правильной
системы а.
mc
имеются две двухкратные правильные
системы точек с нулевыми координатами
X
и Y:
а
и b.
Им соответствуют точечные группы
симметрии позиций Зm
= D3d
и
6m2
= D3h.
Октаэдр может размещаться лишь в той
позиции, группа точечной симметрии
которой является подгруппой Оh
— группы симметрии октаэдра. Это
означает, что в качестве координат
центров октаэдрических пустот мы должны
выбрать координаты точек правильной
системы а.
Четыре тетраэдрические пустоты должны располагаться по одной из четырехкратных частных правильных систем точек f или е. При выборе конкретной правильной системы учтем, что в двухслойной упаковке центр тетраэдра размещается над центром шара, который является вершиной тетраэдра. Это означает, что координаты X и Y тетраэдрической пустоты должны совпадать с соответствующими координатами X и Y шара. Отсюда следует, что в качестве координат тетраэдрических пустот подходит правильная система точек f.
Данная правильная система точек имеет один параметр — координату Z. Это означает, что мы должны выбрать из бесконечного множества таких правильных систем точек одну с некоторым конкретным значением координаты Z. Это можно сделать из чисто геометрических соображений. Представим фрагмент двухслойной упаковки в виде двух соединенных вершинами тетраэдрических пустот (рис.16).

Рис.16. К определению координаты Z центра тетраэдрической пустоты в двухслойной плотнейшей упаковке
Удвоенная высота тетраэдра равна параметру элементарной ячейки с. Под центром тетраэдрической пустоты мы будем понимать точку пересечения всех зеркально-поворотных осей 4-го порядка точечной группы симметрии тетраэдра. Очевидно, что эта точка совпадает с точкой пересечения всех высот тетраэдра. Решая несложную геометрическую задачу, можно получить, что эта точка пересечения делит высоты тетраэдра в пропорции (1/4) : (3/4) = 1:3. Это означает, что координаты Z центров тетраэдрических пустот отличаются от Z-координат шаров на ±1/8.
Таким образом, мы можем окончательно записать координаты шаров, тетраэдрических и октаэдрических пустот в двухслойной плотнейшей упаковке:
