16. Виды уравнений прямой в пространстве. Расстояние от точки до прямой.

Виды:

1) Прямая в пространстве в прямоугольной системе координатOxyzможет быть задана системой из уравнений двух пересекающихся плоскостей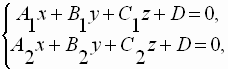

2) Параметрические уравнения прямой в пространстве: 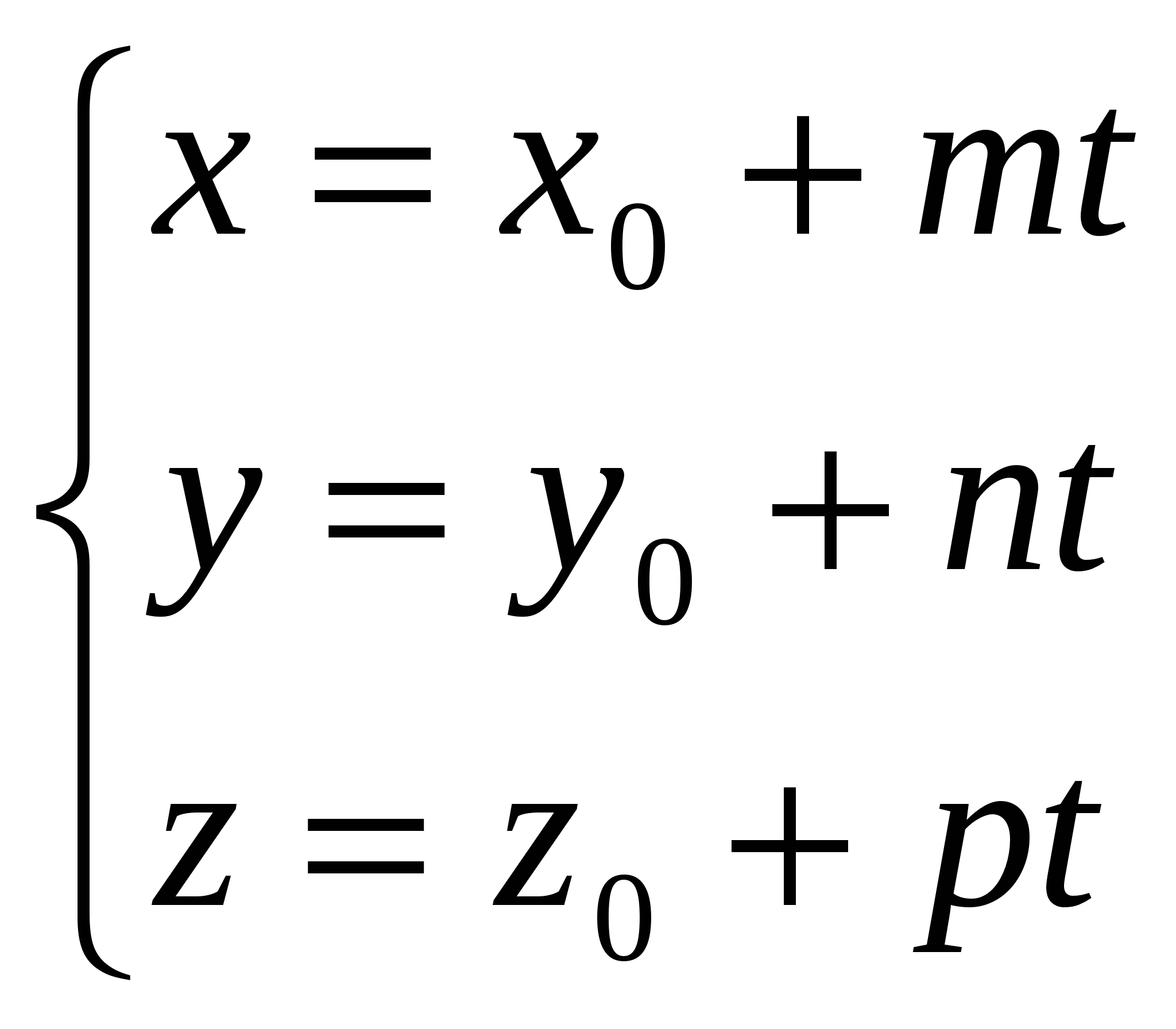гдеx₀,y₀иz₀– координаты некоторой точки прямой,m,n,p- соответствующие координаты направляющего вектора прямой, аt- некоторый параметр.

3) Каноническое уравнение прямой в пространстве:

Расстояние от точки до прямой: 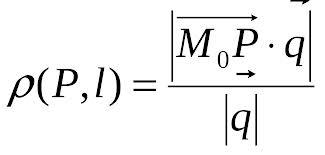,| | 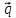- длина вектора прямой,M_o – точка, лежащая на прямой l, P – точка.

17. Взаимное расположение двух прямых в пространстве, угол между прямыми.

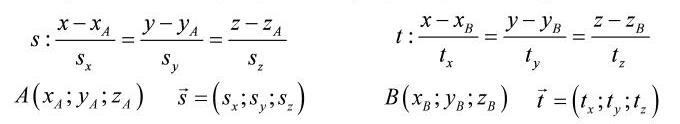
1) Прямые скрещиваются: (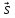,,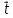) ≠ 0

2) Прямые параллельны: (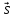,,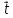) = 0, ||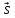

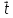
3) Прямые пересекаются (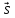,,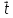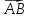) = 0,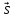 не параллельна

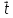
Угол между прямыми aиb: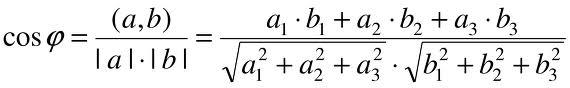

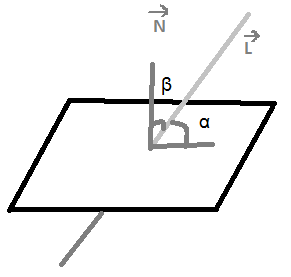
18. Взаимное расположение прямой и плоскости, угол между ними.

Плоскость: A_x + B_y + C_z + D = 0

Прямая:

1) Параллельны: A_l + B_m + C_n = 0

2) Перпендикулярны: = =

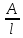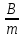3) Прямая лежит в плоскости: A_l + B_m + C_n = 0 и Ax_o + By_o + Cz_o + D = 0

Угол между плоскостью и прямой:

Sin α = cos β = cos () = =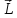

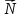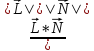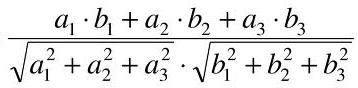
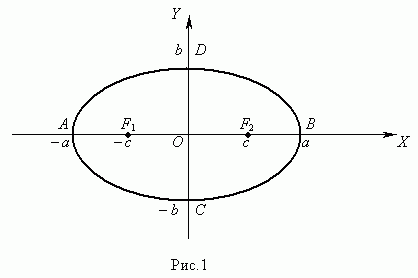
19. Каноническое уравнение эллипса, эксцентриситет, директриса.

Эллипс - геометрическое место точек, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная, бОльшая, чем расстояние между данными точками.

Эксцентриситет - отношение фокусного расстояния к большей оси: E =

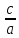
Директрисы эллипса - две прямые, которые в канонической для эллипса системе координат имеют уравнения

20. Канонические уравнение гиперболы, эксцентриситет, директриса, асимптоты.

Гипербола - геометрическое место точек, модуль разности расстояний от которых до двух фиксированных точек (фокусов) есть величина постоянная, мЕньшая, чем расстояния между этими точками.

Эксцентриситет - отношение фокусного расстояния к большей оси: E =

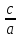
Директрисами гиперболы называются две прямые, уравнения которых в канонической для гиперболы системе координат имеют вид  .

Прямая называется асимптотой кривой, если при удалении от начала координат расстояние между кривой и асимптотой стремится к нулю.

Прямые называются асимптотами гиперболы.

21. Каноническое уравнение параболы

Парабола – геометрическое место точек, равноудалённых от заданной точки, называемой фокусом и от заданной прямой, называемой директрисой.

P – расстояние между фокусом и директрисой параболы.

22. Поверхности 2-го порядка. Эллипсоид. Гиперболоид. Конус.

Общий вид поверхности 2-го порядка: Ax² + By² + Cz² + Dxy + Eyy + Fzx + Lx + My + Nz + K = 0

1) Эллипсоид

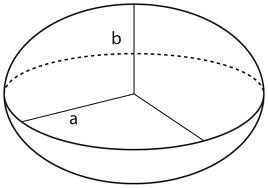
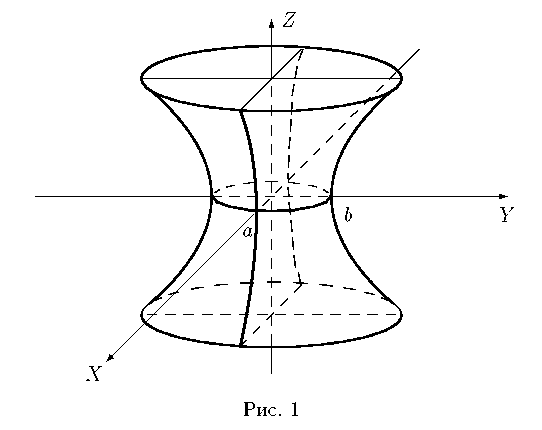
2)Однополостный гиперболоид (рис. 1) -

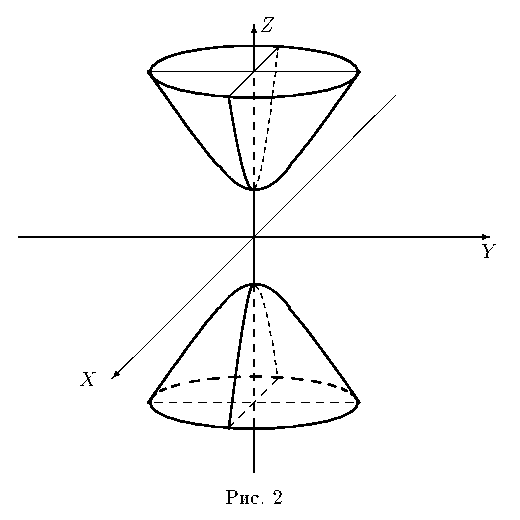
Двуполостный гиперболоид (рис. 2) -

3) Конус

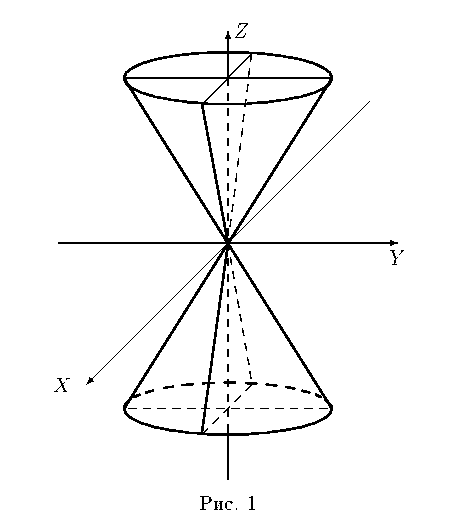
23. Эллиптический и гиперболический параболоиды.

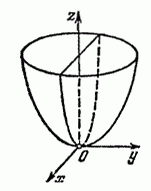
Эллиптический параболоид:

Гиперболический параболоид: 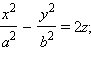a > 0, b >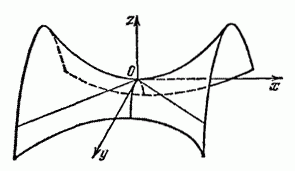

24. Поверхности вращения.

Пусть L – прямая в плоскости P. Будем вращать P вокруг прямой L, тогда точки некоторой кривой в плоскости P будут описывать поверхность, состоящую из окружности. Такая поверхность называется поверхностью вращения.

Каноническое уравнение эллипсоида:

При a = b Получится эллипсоид вращения вокруг оси Oz

При a = c – вокруг оси Oy (рис. 29)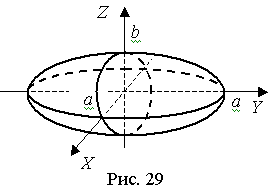

При b = c – вокруг оси Ox

При a = b = c - сфера

25. Цилиндрические поверхности.

Любое уравнение f (x,y) = 0 можно рассматривать как цилиндрическую поверхность с образующей параллельной OZ и направляющей кривой F (x,y) = 0.

Если уравнение F (x,y) = 0 определяет кривую 2-го порядка, то она называется цилиндрической поверхностью 2-го порядка.

1) Эллиптический цилиндр

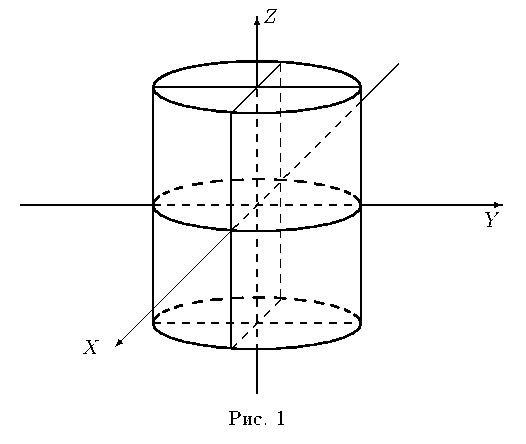
2) Гиперболоид цилиндрический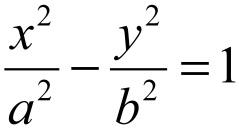

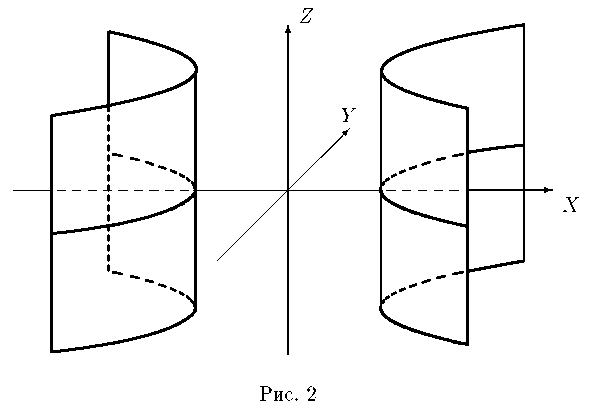
3) Параболический цилиндр: y²= 2px(p>0 )

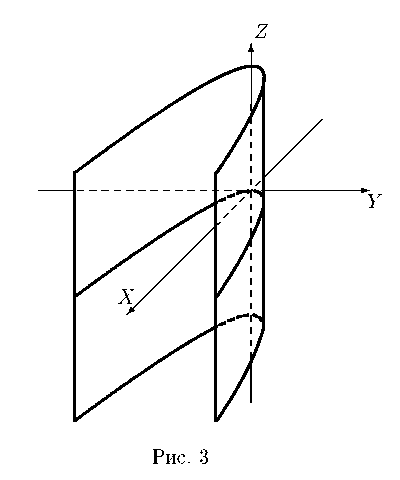
Дифференциальное исчисление функции одной переменной

26. Понятие функции. Способы задания функции. Свойства функций. Обратная функция.

Пусть x,y≠ 0. Функция – соответствиеf, по которому любойx, принадлежащий множествуXсопоставлено единственномуy, принадлежащему множествуY.y=f(x)

Способы задания функции:

1) Аналитический

2) Табличный

3) Графический

4) Словесный

Свойства функции:

1) чётность/нечётность чётная (симметрична относительно Oy), еслиf(-x) =f(x);

нечётная (симметрична относительно начала координат), если f(-x) = -f(x)

2) Возрастание\убывание

3) Ограниченность. f(x) ограничена, если существуетM> 0, такое, чтоf(x) <M(илиf(x) >M, если ограничена снизу) при любомx.

4) Периодичность. Функция f(x) называется периодической с периодомT> 0, еслиf(x) =f(x+T), при любомx.

Пусть X– область определения, аY– область значений функцииf. Если для любогоyиз области значений существует единственныйx, принадлежащий области определения, то говорят, что определена обратная функция кy=f(x) (f^-1)

Любая монотонная функция обладает обратной функцией.

Геометрический смысл: Функция и обратная к ней функция симметрична относительно y=x.