- •Элементы линейной алгебры
- •1. Операции над матрицами. Свойства операций.
- •2. Определители 2-го и 3-го порядков. Минор и алгебраическое дополнение. Определитель n-го порядка. Свойства определителей.
- •3. Обратная матрица. Теорема существования обратной матрицы.
- •4. Системы линейных уравнений. Матричная запись системы. Формулы Крамера.
- •5. Однородная система линейных уравнений и свойства ее решений.
- •6. Решение систем методом Гаусса.
- •Векторная алгебра
- •7. Линейные операции над векторами. Базис.
- •8. Проекция вектора на ось. Прямоугольная система координат. Координаты точки. Линейные операции над векторами в координатной форме.
- •9. Скалярное произведение векторов, его свойства. Вычисление в координатах.
- •10. Определение правой тройки векторов. Векторное произведение векторов, его свойства, геометрический смысл.
- •11. Смешанное произведение 3-х векторов, его свойства. Геометрический смысл. Вычисление в координатах. Необходимое и достаточное условие компланарности 3-х векторов.
- •16. Виды уравнений прямой в пространстве. Расстояние от точки до прямой.
- •17. Взаимное расположение двух прямых в пространстве, угол между прямыми.
- •18. Взаимное расположение прямой и плоскости, угол между ними.
- •19. Каноническое уравнение эллипса, эксцентриситет, директриса.
- •20. Канонические уравнение гиперболы, эксцентриситет, директриса, асимптоты.
- •21. Каноническое уравнение параболы
- •27. Основные элементарные функции и их графики.
- •28. Предел числовой последовательности. Бесконечно большие и бесконечно малые числовые последовательности. Свойства бесконечно малых.
- •29. Основные теоремы о пределах последовательностей.
- •30. Первый и второй замечательные пределы. Число е.
- •31. Предел функции. Основные теоремы о пределах функций.
- •32. Замечательные пределы для функций.
- •33. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •34. Непрерывные функции. Классификация точек разрыва.
- •35. Свойства непрерывных функций. Основные теоремы о непрерывных функциях.
- •36. Определение производной, ее геометрический смысл.
- •37. Дифференцируемость и непрерывность. Правила дифференцирования.
- •38. Производная сложной функции, функции, заданной неявно, заданной параметрически, обратной функции.
- •39. Производные основных элементарных функций.
- •41. Производные и дифференциалы высших порядков.
- •42. Теорема Ферма. Теорема Ролля.
- •43. Теорема Лагранжа и следствия из нее. Теорема Коши.
- •44. Правило Лопиталя.
- •45. Возрастание и убывание дифференцируемой функции. Необходимые и достаточные условия.
- •46. Экстремум дифференцируемой функции. Необходимые и достаточные условия.
- •47. Теорема (второе достаточное условие экстремума).
- •48. Выпуклость функции. Необходимые и достаточные условия выпуклости. Точки перегиба.
- •49. Асимптоты графика функций.
10. Определение правой тройки векторов. Векторное произведение векторов, его свойства, геометрический смысл.
Тройка
векторов
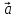 ,
,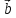 и
и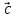 называется правой, если
называется правой, если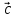 направлен так, что из его конца кратчайший
поворот от
направлен так, что из его конца кратчайший
поворот от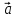 к
к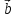 происходит против часовой стрелки.
происходит против часовой стрелки.
Векторным
произведением вектора
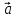 на вектор
на вектор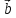 называется третий вектор
называется третий вектор который обладает следующими свойствами:
который обладает следующими свойствами:
Его длина равна
![]()
Вектор
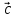 перпендикулярен к плоскости, в которой
лежат вектора
перпендикулярен к плоскости, в которой
лежат вектора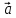 и
и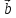
Вектор
 направлен так, что поворот от вектора
направлен так, что поворот от вектора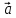 к вектору
к вектору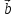 осуществляется против часовой стрелки,
если смотреть из конца вектора
осуществляется против часовой стрелки,
если смотреть из конца вектора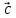 (тройка векторов
(тройка векторов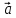 ,
,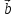 и
и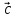 – правая).
– правая).
Основные свойства векторного произведения:
1)
Векторное произведение
![]() равно
нулю, если векторы
равно
нулю, если векторы![]() и
и![]() коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2)
При перестановке местами векторов
сомножителей векторное произведение
меняет знак на противоположный
![]()
![]()
![]()
Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.
11. Смешанное произведение 3-х векторов, его свойства. Геометрический смысл. Вычисление в координатах. Необходимое и достаточное условие компланарности 3-х векторов.
Смешанным произведением векторов
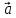 ,
,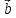 ,
,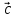 называется число, равное (
называется число, равное (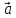 *
*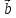 )*
)*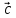 = (
= (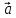 ,
,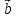 ,
,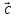 )
)
Модуль смешанного произведения векторов
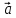 ,
,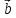 ,
,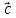 равен объёму параллелепипеда, построенного
на векторах
равен объёму параллелепипеда, построенного
на векторах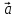 ,
,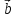 ,
,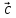 .
.
Свойства:
1)
(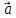 *
*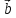 )*
)*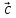 =
=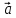 *(
*(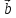 *
*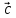 )
)
2)
(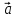 ,
,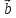 ,
,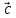 )
= (
)
= (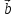 ,
,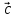 ,
,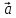 )
= (
)
= (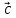 ,
,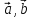 )
= - (
)
= - (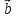 ,
,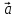 ,
,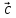 )
= ... циклически меняем
)
= ... циклически меняем
3)
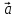 ,
,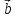 ,
,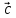 – компланарны (
– компланарны (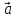 ,
,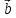 ,
,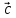 )
= 0
)
= 0
4)
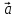 ,
,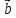 ,
,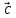 – правая (
– правая (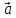 ,
,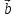 ,
, )
> 0
)
> 0
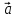 ,
,
 ,
,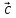 – левая (
– левая (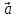 ,
,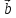 ,
,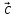 )
< 0
)
< 0
5)
(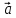 1+
1+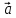 2,
2,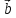 ,
,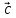 )
= (
)
= (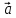 1,
1,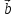 ,
,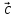 )
+ (
)
+ (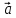 2,
2, ,
,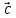 ) (α*
) (α*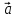 ,
,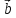 ,
,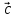 )
= α(
)
= α(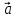 ,
,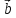 ,
,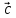 )
)
Вычисление
в координатах: 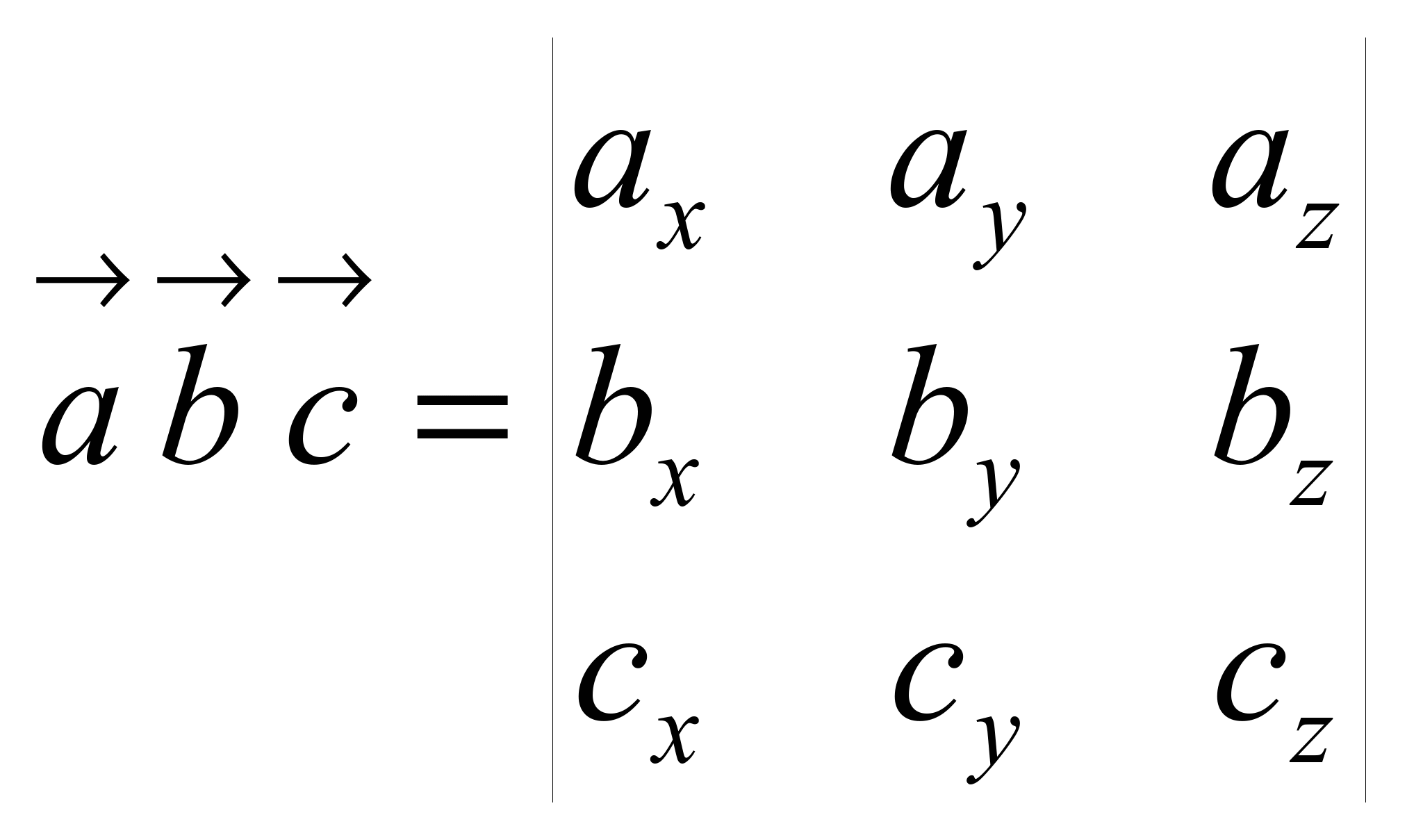
Необходимое
и достаточное условие компланарности
3-х векторов :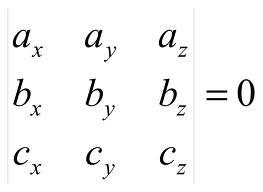
Аналитическая геометрия
12. Виды уравнений прямой на плоскости. Расстояние от точки до прямой.

Виды:
1) Общее уравнение прямой: Ax + By + C = 0
2)
Уравнение прямой в отрезках:
![]()
3) Уравнение прямой с угловым коэффициентом: y = kx + b
4)
Каноническое уравнение прямой на
плоскости: ![]()
5)
Параметрические уравнения прямой на
плоскости:
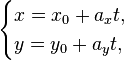
6)
Нормальное уравнение прямой:
![]()
![]()
![]()
![]()
![]()
![]()
![]() p- длина перпендикуляра,
опущенного из начала координат на
прямую, β- угол наклона этого перпендикуляра к
осиO.
p- длина перпендикуляра,
опущенного из начала координат на
прямую, β- угол наклона этого перпендикуляра к
осиO.
Расстояние точки A(x1, y1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле:
![]()
![]()
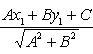
![]()
13. Взаимное расположение двух прямых на плоскости, угол между прямыми.
Если
прямые
![]() и
и![]() заданы
общими уравнениями
заданы
общими уравнениями![]() и
и![]() ,
,
тогда
угол между ними находится по формуле:
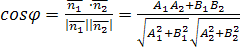
![]() –условие параллельности
прямых
–условие параллельности
прямых
![]() и
и![]() ;
;
![]() –условие перпендикулярности
прямых
–условие перпендикулярности
прямых
![]() и
и![]() .
.
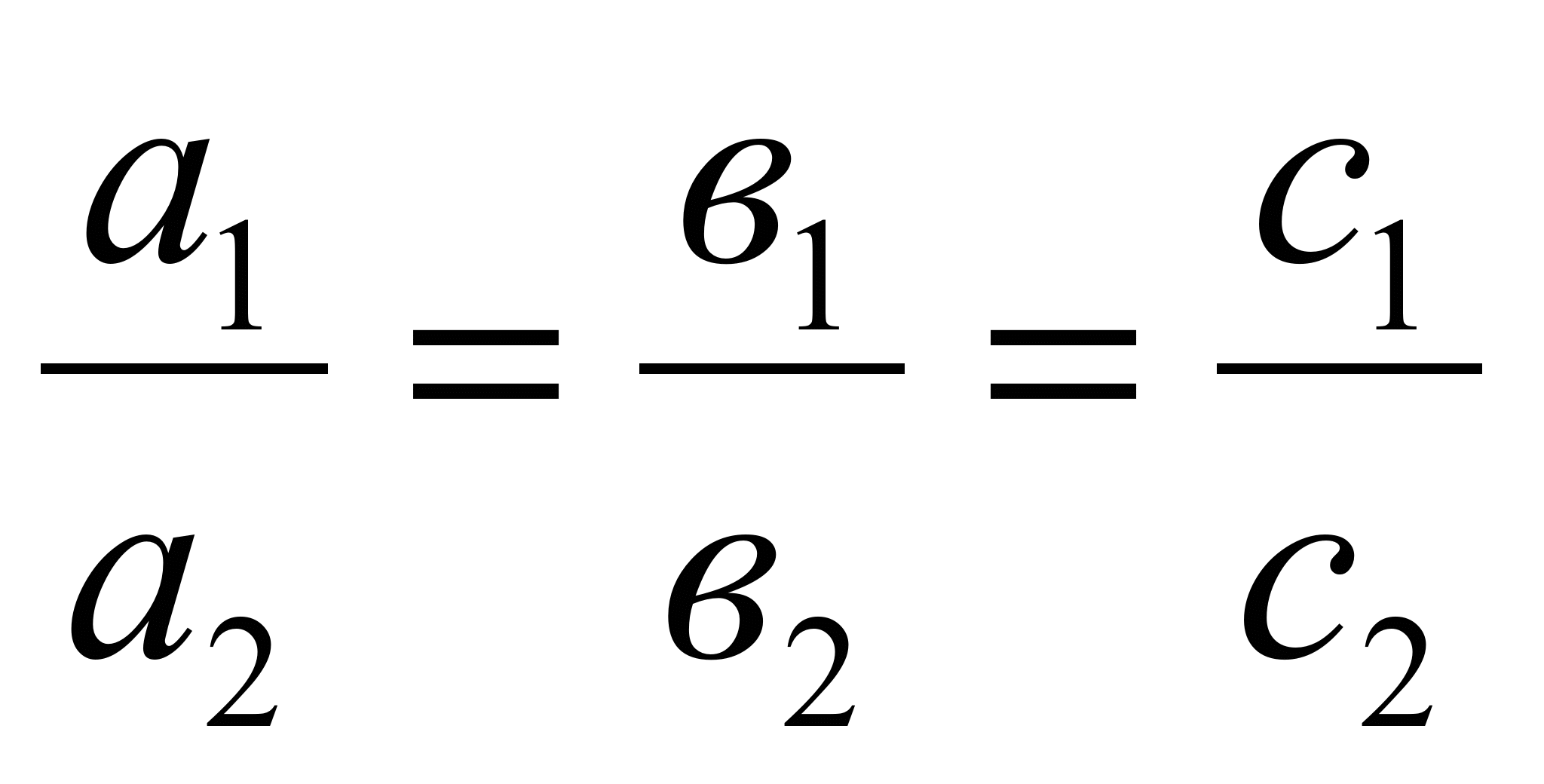 - прямые совпадают.
- прямые совпадают.
14. Виды уравнений плоскости. Расстояние от точки до плоскости.
Виды уравнений плоскости:
1) Общее: Ax + By + Cz + D = 0
2)
В отрезках:
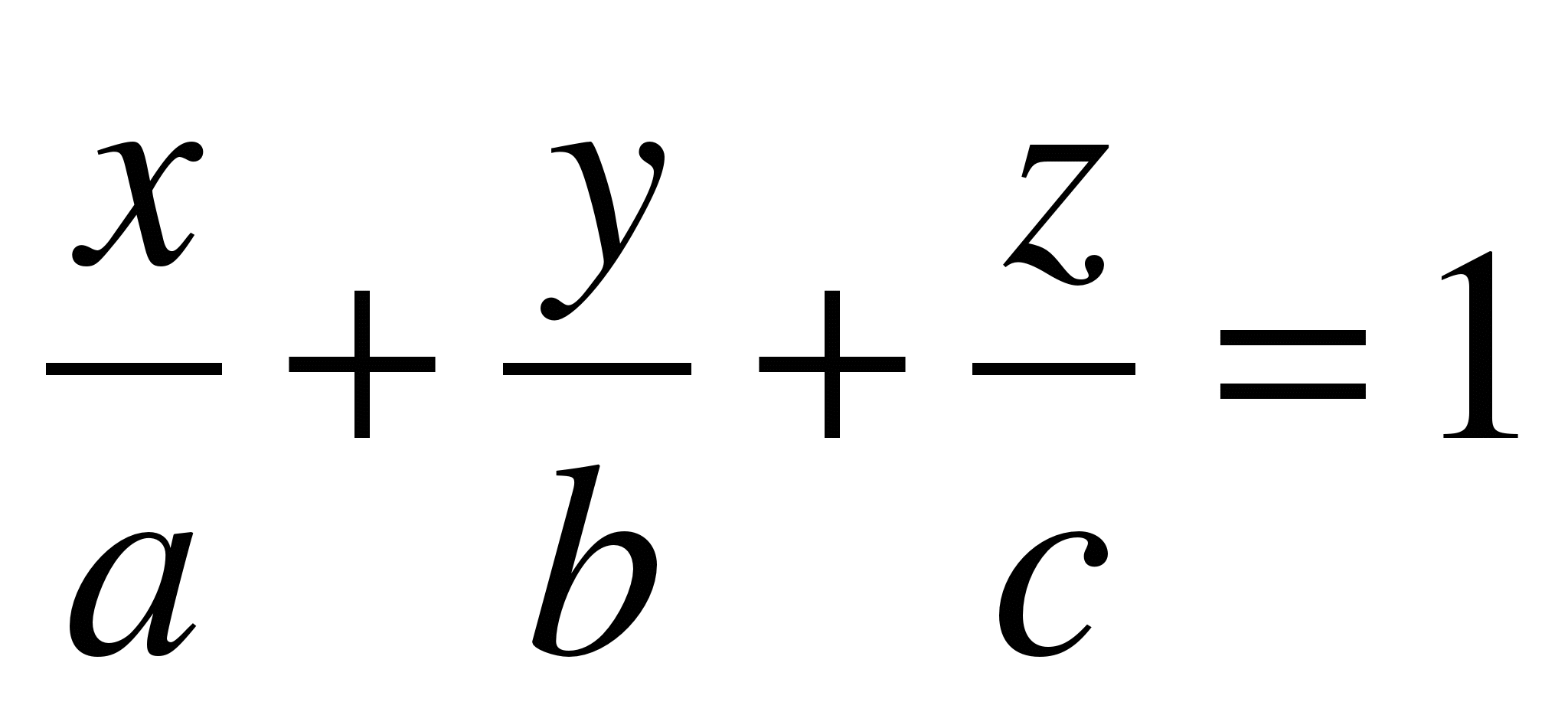
3)
Нормальное:
![]()
Пусть плоскость
![]() задана
уравнениемAx
+ By
+ Cz
+ D
= 0 и дана
точка
задана
уравнениемAx
+ By
+ Cz
+ D
= 0 и дана
точка
![]() .
Тогда расстояниеp
от точки Mo
до плоскости
.
Тогда расстояниеp
от точки Mo
до плоскости
![]() определяется
по формуле
определяется
по формуле
|
|
15. Взаимное расположение двух плоскостей, угол между плоскостями.
Взаимное расположение двух плоскостей характеризуется двумя возможностями^
1) Две плоскости не имеют общих точек, и , в таком случае, они называются параллельными
2) Две плоскости имеют хотя бы одну общую точку, и в таком случае они называются пересекающимися.
Пусть
наши плоскости ![]() и
и![]() заданы
уравнениями:
заданы
уравнениями:
![]() :
:
![]()
![]() :
:![]()
Косинус
угла ![]() между плоскостями находится по такой
формуле:
между плоскостями находится по такой
формуле:
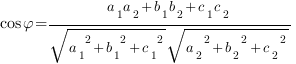
1)
Плоскости параллельны:
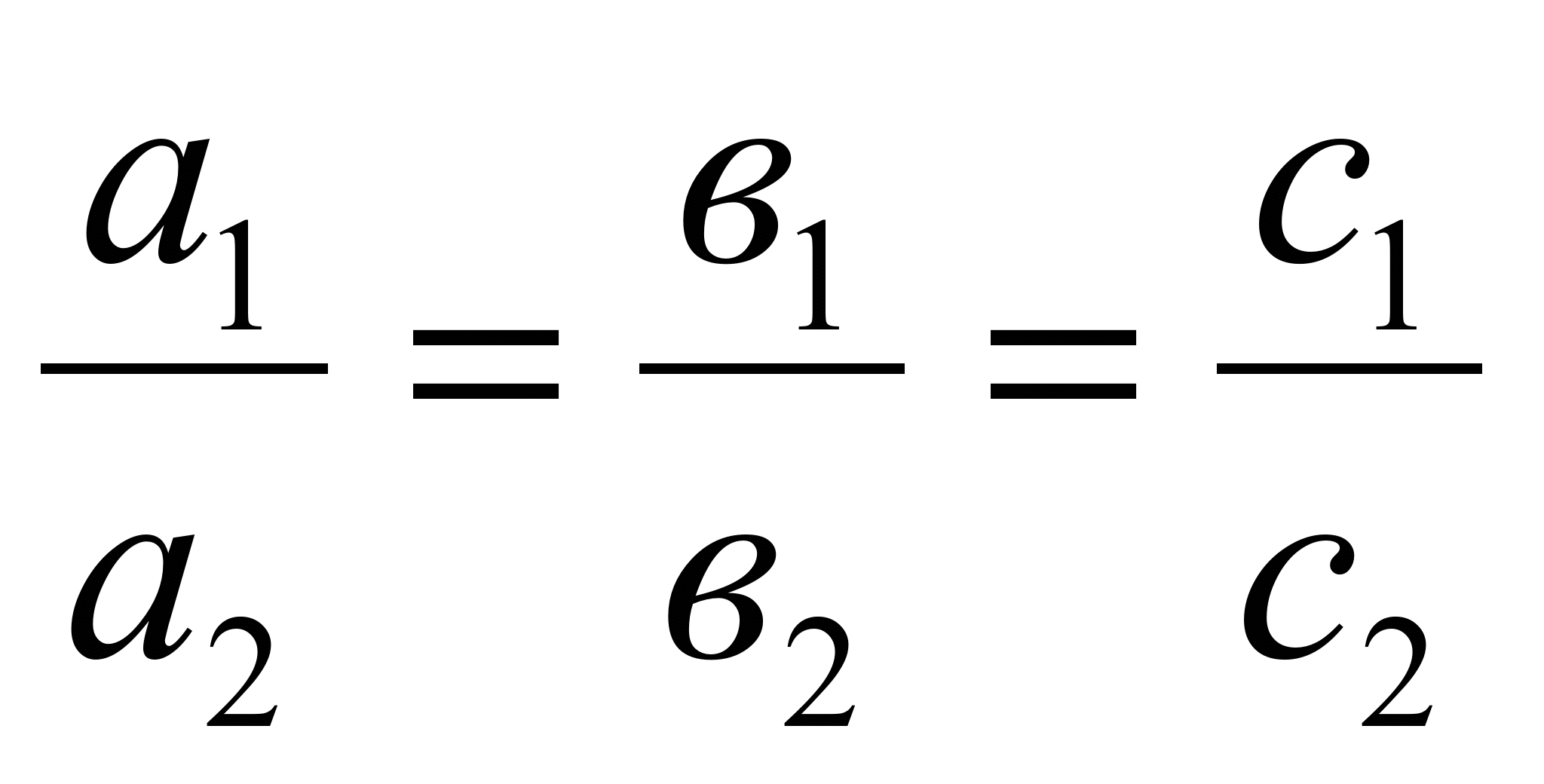
2) Плоскости совпадают, если выполняются следующие условия:
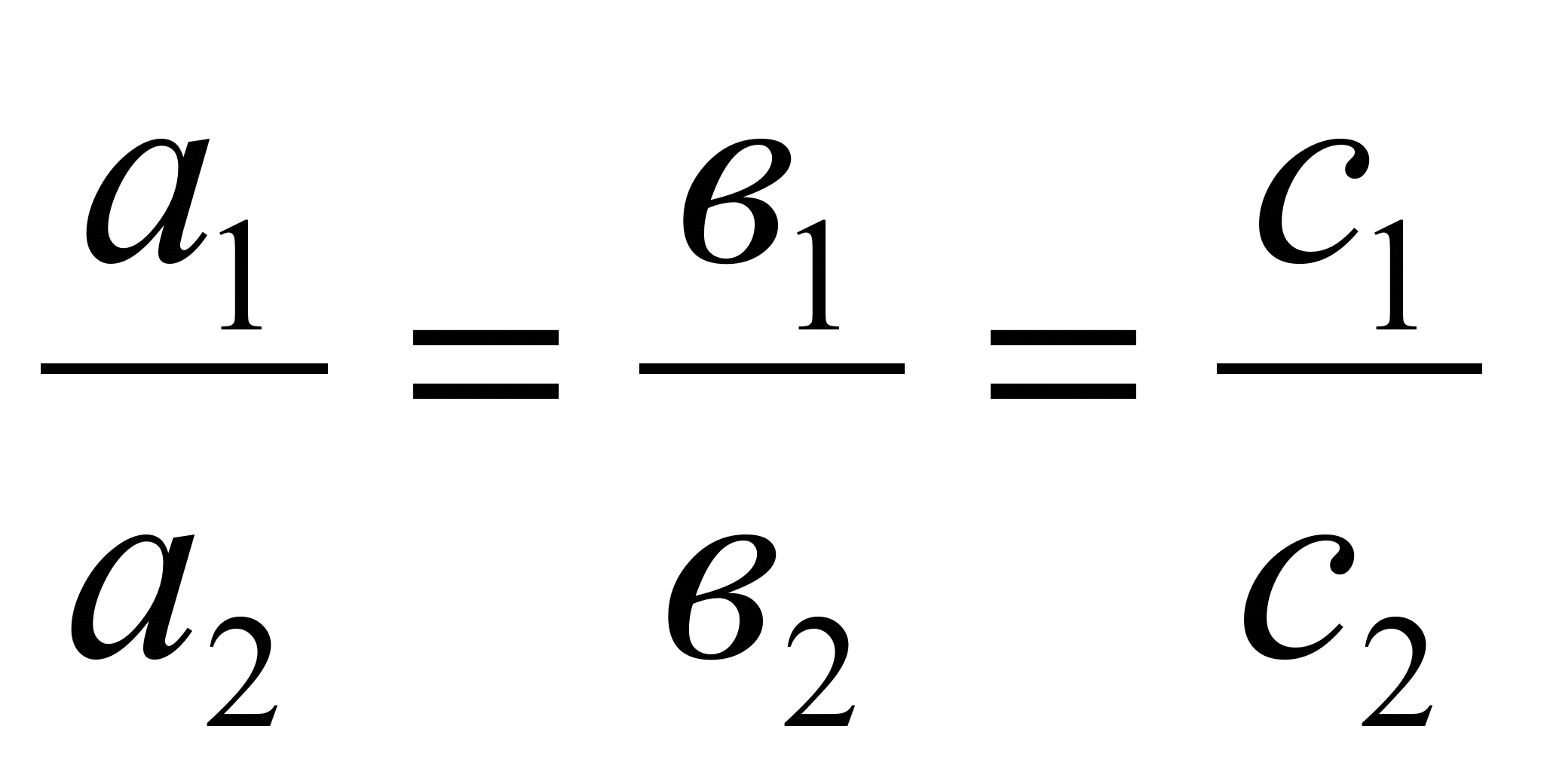
a2*x0 + b2*y0 + c2*z0 + d2 = 0
существует точка M0(x0,y0,z0), принадлежащая плоскости П1