- •Элементы линейной алгебры
- •1. Операции над матрицами. Свойства операций.
- •2. Определители 2-го и 3-го порядков. Минор и алгебраическое дополнение. Определитель n-го порядка. Свойства определителей.
- •3. Обратная матрица. Теорема существования обратной матрицы.
- •4. Системы линейных уравнений. Матричная запись системы. Формулы Крамера.
- •5. Однородная система линейных уравнений и свойства ее решений.
- •6. Решение систем методом Гаусса.
- •Векторная алгебра
- •7. Линейные операции над векторами. Базис.
- •8. Проекция вектора на ось. Прямоугольная система координат. Координаты точки. Линейные операции над векторами в координатной форме.
- •9. Скалярное произведение векторов, его свойства. Вычисление в координатах.
- •10. Определение правой тройки векторов. Векторное произведение векторов, его свойства, геометрический смысл.
- •11. Смешанное произведение 3-х векторов, его свойства. Геометрический смысл. Вычисление в координатах. Необходимое и достаточное условие компланарности 3-х векторов.
- •16. Виды уравнений прямой в пространстве. Расстояние от точки до прямой.
- •17. Взаимное расположение двух прямых в пространстве, угол между прямыми.
- •18. Взаимное расположение прямой и плоскости, угол между ними.
- •19. Каноническое уравнение эллипса, эксцентриситет, директриса.
- •20. Канонические уравнение гиперболы, эксцентриситет, директриса, асимптоты.
- •21. Каноническое уравнение параболы
- •27. Основные элементарные функции и их графики.
- •28. Предел числовой последовательности. Бесконечно большие и бесконечно малые числовые последовательности. Свойства бесконечно малых.
- •29. Основные теоремы о пределах последовательностей.
- •30. Первый и второй замечательные пределы. Число е.
- •31. Предел функции. Основные теоремы о пределах функций.
- •32. Замечательные пределы для функций.
- •33. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
- •34. Непрерывные функции. Классификация точек разрыва.
- •35. Свойства непрерывных функций. Основные теоремы о непрерывных функциях.
- •36. Определение производной, ее геометрический смысл.
- •37. Дифференцируемость и непрерывность. Правила дифференцирования.
- •38. Производная сложной функции, функции, заданной неявно, заданной параметрически, обратной функции.
- •39. Производные основных элементарных функций.
- •41. Производные и дифференциалы высших порядков.
- •42. Теорема Ферма. Теорема Ролля.
- •43. Теорема Лагранжа и следствия из нее. Теорема Коши.
- •44. Правило Лопиталя.
- •45. Возрастание и убывание дифференцируемой функции. Необходимые и достаточные условия.
- •46. Экстремум дифференцируемой функции. Необходимые и достаточные условия.
- •47. Теорема (второе достаточное условие экстремума).
- •48. Выпуклость функции. Необходимые и достаточные условия выпуклости. Точки перегиба.
- •49. Асимптоты графика функций.
5. Однородная система линейных уравнений и свойства ее решений.
Однородной системой m линейных уравнений с n неизвестными называется система вида
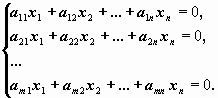
Свойства решений:
Теорема 1. Линейная комбинация решений однородной системы является решением системы.
Теорема 2. Разность двух решений неоднородной системы является решением однородной системы.
Теорема 3. Сумма решения однородной системы с решением неоднородной системы есть решение неоднородной системы.
6. Решение систем методом Гаусса.
Метод Гаусса заключается в последовательном исключении неизвестных с помощью следующих преобразований:
1) Умножение уравнения на число, отличное от нуля.
2) Прибавление к одному уравнению другого, умноженного на число.
3) Перемена местами уравнений.
4) Замена местами неизвестных.
С помощью этих преобразований система сводится к системе трапецеидального вида.
Векторная алгебра
7. Линейные операции над векторами. Базис.
Вектор – направленный отрезок прямой, у которого один конец – начало, а другой – конец.
Линейные операции над векторами:
1) Умножение вектора на число.
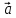 ,
α
ϵ
R
=>
,
α
ϵ
R
=>
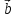 =α
*
=α
*
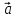
1)
|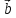 |
= |α|*|
|
= |α|*|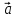 |
|
2)
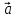 ||
||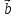
3)
α
> 0 =>
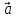 ↑↑
↑↑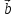
α
< 0 =>
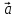 ↑↓
↑↓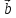
α
= 0 =>
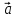 =
=
2) Сложение векторов. Складываются по правилу треугольника или параллелограмма.
свойства:
1)
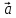 +
+
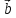 =
=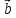 +
+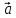
2)
(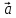 +
+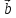 )
+
)
+ =
=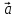 + (
+ (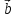 +
+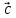 )
)
3)
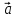 +
+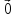 =
=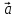
4)
-
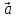 = (-1)*
= (-1)*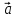
5)
α
(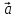 +
+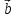 )
=α*
)
=α*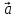 + α*
+ α*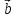 ,
α
ϵ
R
,
α
ϵ
R
6)
(α
+ β) = α*
= α*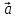 +
+
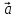 *β
*β
3) Разность векторов.
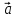 -
-
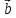 =
=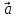 + (-1)*
+ (-1)*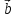 =
=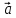 *β
*β
Базис – упорядоченный набор компланарных векторов в пространстве.
Представление
вектора в виде линейной комбинации
векторов называется разложением вектора
по базису, а коэффициент этого разложения
– координатами вектора
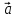 в
этом базисе.
в
этом базисе.
![]()
![]() - базисы трёхмерного пространства.
- базисы трёхмерного пространства.
8. Проекция вектора на ось. Прямоугольная система координат. Координаты точки. Линейные операции над векторами в координатной форме.
Свойства проекций:
1)
Проеция вектора
![]() на
осьl
равна произведению модуля вектора
на
осьl
равна произведению модуля вектора
![]() на
косинус угла между вектором и осью:
на
косинус угла между вектором и осью:
![]()
2)
Проекция суммы двух векторов
на ось равна сумме проекций векторов
на ту же ось:![]()
3)
Если вектор![]() умножается
на число λ, то его проекция на ось также
умножается на это число
умножается
на число λ, то его проекция на ось также
умножается на это число
ПСК
– система координат с базисом
 ,
,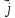 ,
,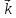 ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
1)
|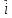 |
= |
|
= |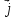 |
= |
|
= |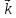 |
= 1
|
= 1
2)
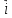 ,
,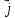 ,
,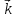 перпендикулярны друг другу.
перпендикулярны друг другу.
Координаты точки: Пусть a,b,
c– единичные
векторы осей координат,O– начало
координат. Тогда координаты произвольной
точкиP– это координаты вектора![]() относительно
базиса (a,b, c).
относительно
базиса (a,b, c).
Линейные операции над векторами в координатной форме:
1. Равные векторы имеют равные координаты (в одном и том же базисе).
2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.
3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.
4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.
9. Скалярное произведение векторов, его свойства. Вычисление в координатах.
Скалярным произведением векторов
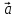 и
и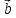 называется произведение их длин на
косинус угла между ними:
называется произведение их длин на
косинус угла между ними:![]()
Свойства:
1)
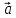 *
*
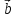 =
=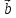 *
*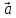
2)
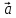 (α
*
(α
*
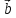 )
= (α*
)
= (α*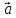 )*
)*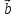 = α*(
= α*(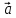 *
*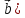
3)
(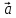 +
+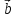 )
*
)
*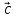 =
=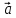 *
*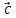 +
+
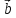 *
*
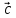
4)
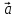 *
*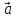 = |
= |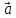 |2
|2
5)
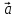 ,
,
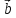 ≠
≠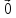
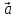 *
*
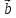 > 0 0 < угол (
> 0 0 < угол (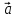 ;
;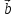 )
<
)
<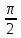
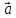 *
*
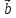 < 0
< 0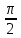 < угол (
< угол (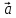 ;
;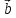 )
<π
)
<π
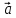 *
*
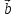 = 0
= 0 перпендикулярен
перпендикулярен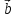
![]()
![]()
![]()
![]()