2Отрицательная матрица
Эрмитова
матрица
M
размерности
будет
называться отрицательно
определённой,
если
для
всех ненулевых
(или,
эквивалентным образом, для всех ненулевых
).
M будет называться положительно полуопределённой, если
для
всех
(или,
эквивалентным образом, для всех
).
M будет называться отрицательно полуопределённой, если
для
всех
(или,
эквивалентным образом, для всех
).
Таким образом, матрица будет отрицательно определённой, если все её собственные значения отрицательны, положительно полуопределённой, если все её собственные значения неотрицательны, и отрицательно полуопределённой, если все её собственные значения неположительны.
Матрица M будет положительно полуопределённой тогда и только тогда, когда она является матрицей Грама какого-нибудь множества векторов. В отличие от положительно определённой матрицы данные векторы не обязательно линейно независимы.
Для
любой матрицы A
выполняется следующее: A
*
A
— положительно полуопределённая, а
.
Обратное утверждение также верно: любая
положительно полуопределённая матрица
M
может быть выражена как M
= A
*
A
(разложение
Холецкого).
Эрмитова матрица не являющаяся ни положительно, ни отрицательно полуопределённой называется неопределённой.
3Элементарные преобразования матрицы.Вырожденные и невырожденные.
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к элемнтам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование;
Те же операции, применяемые для столбцов, также называются элементарными преобразованиями.
С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк ( столбцов ).
Вы́рожденнойилисингуля́рнойназывают квадратнуюматрицу,определителькоторой равен нулю.
Эквивалентные условия вырожденности
Используя различные понятия линейной алгебры, можно привести различные условия вырожденности:
Строки или столбцы матрицы линейно зависимы.
Квадратная матрица A вырождена тогда и только тогда, когда существует ненулевой вектор x, такой, что Ax = 0. Иными словами, линейный оператор, соответствующий матрице в стандартном базисе, имеет ненулевое ядро.
Свойства
У матрицы нет стандартной обратной матрицы, но есть обобщённая обратная матрица (или их бесконечное количество
4 Минора и алгеброические дополнения
Минором
элемента
матрицы n-го
порядка называется определитель матрицы
(n-1)-го
порядка, полученный из матрицы А
вычеркиванием i-й
строки и j-го
столбца.
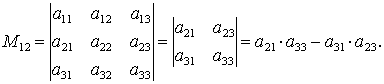
При выписывании определителя (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.
Пример
1.
Составить минор
,
полученную из исходной матрицы:
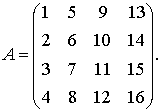
Решение:
.
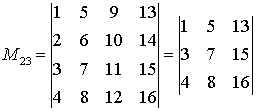Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Пример 1. Найти алгебраические дополнения всех элементов матрицы
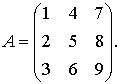
Решение:
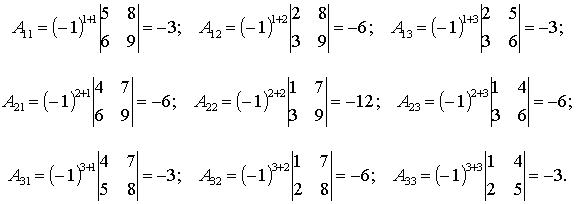
5ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ, ДЕТЕРМИНАНТ[determinant] — число, соответствующееквадратной матрицеи полученное путем ее преобразования по определенному правилу. Обычное обозначение (для матрицыA): detA.Напр., определитель (второго порядка) матрицы
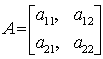
обозначается
и вычисляется следующим образом:
det A=a11a22—a12a21.
В общем случае (для квадратной матрицы порядка n) изэлементовматрицыAсначала составляют все возможные произведения изnсомножителей каждое, содержащие по одному элементу из каждой строки и по одному элементу из каждого столбца, затем эти произведения складываются по определенному правилу.
Определитель матрицы, в которой вычеркнуты произвольная строка (напр. i-я), и произвольный столбец (напр.j-й), называетсяминором.Он имеет (n– 1)-й порядок, т. е. порядок на 1 меньше, нежели исходный определитель.
Определители используются при обращении матриц(см. такжеАлгебраическое дополнение), при решениисистем линейных уравнений, в частности при решении задачмежотраслевого баланса.