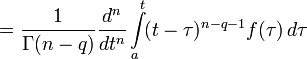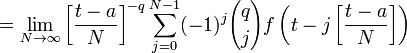38Эйлера подстановки

Эйлера подстановки,подстановки, служащие для приведения интегралов вида

,

где и R (x,y) — рациональная функция отхиу, к интегралам от рациональных функций (см.Интегральное исчисление).Предложены Л.Эйлеромв 1768. Первая Э. п.

применима, если а>0; вторая Э. п.

применима, если с > 0; третья Э. п.

где l — один из корней трёхчлена ax²+bx + c, применима, если корни этого трёхчлена действительны. На практике Э. п. требуют громоздких преобразований и потому вместо них обычно пользуются теми или иными искусств. приёмами, упрощающими вычисление.

Аналогичные подстановки делаются в теории чисел при решении неопределённых уравнений 2-й степени в рациональных числах.

39Определения

Три наиболее употребительных формулы:

• Интегро-дифференцирование Римана-Лиувилля

Самая простая и часто употребляемая формулировка. Эта формула является обобщением до произвольного порядка формулы повторного интегрирования Коши.

• Производная Грюнвальда-Летникова

• Интегро-дифференцирование Вейля

Формально похоже на интегро-дифференцирование Римана-Лиувилля, но распространяется на периодические функции с равным нулю интегралом по периоду.

Обозначим непрерывное преобразование Фурье, как:

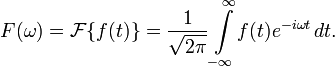
В фурье-пространстве дифференцированию соответствует произведение:

Поэтому,

что сводится к

При преобразовании Лапласа, здесь обозначенном, дифференцирование заменяется умножением

Обобщая для произвольного порядка дифференцирования и решая уравнение относительно D^qf(t), получаем

• Линейность

• Правило нуля

• Дробное интегро-дифференцирование произведения

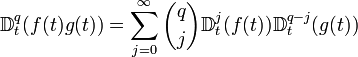
• Полугрупповое свойство

в общем случае не выполняется ^[1].

• 

• 

• 

40Универсальная тригонометрическая подстановка Рассмотрим интегрирование выражений полностью зависящих от тригонометрических функций, над которыми выполняются лишь арифметические операции. Такие выражения называются рациональными функциями от тригонометрических функций и в данном случае обозначаются . Например,,,. В то же время функциярациональной не является.Теорема. Интеграл вида с помощью подстановкипреобразуется в интеграл от рациональной дроби. Для доказательства выразим ,ичерез: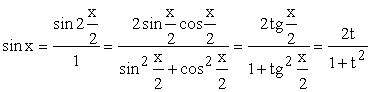;;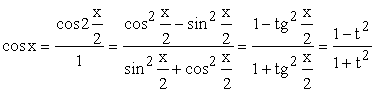. В результате проведенных преобразований,ипревратились в рациональные дроби от. Подставляя их в исходный интеграл, получаем: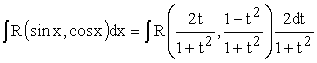. В данном выражении рациональные дроби подставлены в рациональную функцию. Так как над ними выполняются лишь арифметические операции, то в результате получается также рациональная дробь. Итак, рациональную функцию от тригонометрических функций можно проинтегрировать, превратив ее в рациональную дробь. Подстановка,,,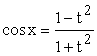называется универсальной тригонометрической подстановкой.2. Частные случаи интегрирования выражений, содержащих тригонометрические функции Рассмотренная в п. 11 универсальная тригонометрическая подстановка позволяет вычислить любой интеграл от функции вида . Однако на практике она часто приводит к слишком сложным рациональным функциям, интегрирование которых представляет значительную трудность. Есть целый ряд интегралов от тригонометрических функций, которые можно вычислить значительно проще. 1. Интегралы типаудобно вычислять с помощью подстановки. Тогдаи получаем простой интеграл. 2. Интегралы типаудобно вычислять с помощью подстановки. Тогдаи интеграл приводится к виду. 3. Если подынтегральная функция зависит только от(), то удобна замена. В этом случаеи. В результате получаем. 4. Если подынтегральная функция является рациональной относительно четных степенейи, то есть, то в этом случае также удобна замена. При этом: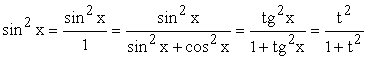;;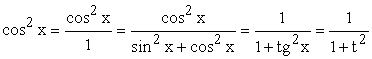. Данная подстановка в этом случае дает более простую рациональную дробь, чем с использованием универсальной тригонометрической подстановки. Пусть дан интеграл, гдеи при этом хотя бы одно из этих чисел нечетное. Допустим, что. ТогдаДалее делается замена, и получаем. 6. Пусть дан интеграл, гдеинеотрицательные и четные. Положим, что,. Тогда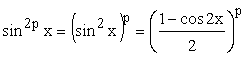;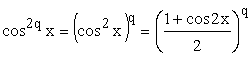. Данная замена позволяет в два раза понизить степень тригонометрических функций. Раскрывая скобки в интеграле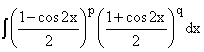, получаем снова случаи 5 или 6. 7. Пусть дан, гдеи– четные и хотя бы одно из этих чисел отрицательно. Тогда удобна та же замена, что и в случае 4. 8. В случаеиспользуется тригонометрическая формулаи интеграл превращается в два табличных интеграла. 9. В случаеиспользуется тригонометрическая формула. 10. В случаеиспользуется тригонометрическая формула