
- •«Конформные отображения»
- •1. Геометрический смысл производной функции комплексного переменного.
- •2. Понятие конформного отображения.
- •3. Общие свойства конформных отображений
- •4. Основные функции.
- •4.1 Линейная функция.
- •4.2 Дробно-линейная функция.
- •4.3 Степенная функция. Понятие римановой поверхности.
- •4.4 Показательная и логарифмическая функции
- •4.5 Общая степенная и тригонометрические функции. Функция Жуковского
- •1. Эйдерман в. Я. «Основы теории функций комплексного переменного и операционного исчисления.»
- •2. Свешников а. Г., Тихонов а. Н. «Теория функций комплексной переменной»
4.5 Общая степенная и тригонометрические функции. Функция Жуковского
1.
Общая степенная функция ![]() ,
где
,
где ![]() — фиксированное комплексное число,
определяется соотношением
— фиксированное комплексное число,
определяется соотношением ![]() .
.
Полагая
![]() ,
получаем Ln z = ln
r + i(φ
+ 2πk).
Следовательно,
,
получаем Ln z = ln
r + i(φ
+ 2πk).
Следовательно,
![]() .
.
Отсюда
видно, что при![]() модуль
модуль
![]() принимает бесконечное множество
значений. Таким образом, при
принимает бесконечное множество
значений. Таким образом, при ![]() функция
функция ![]() будет бесконечнозначной.
будет бесконечнозначной.
Общая
степенная функция ![]() в силу своего определения допускает
выделение регулярных ветвей в тех же
областях, что и логарифмическая; например
в плоскости с разрезом по лучу. Ветвь
в силу своего определения допускает
выделение регулярных ветвей в тех же
областях, что и логарифмическая; например
в плоскости с разрезом по лучу. Ветвь
![]() ,
выделенная в плоскости с разрезом вдоль
отрицательной полуоси, называется
главной ветвью степенной функции. В
силу теоремы о производной сложной
функции для каждой регулярной ветви
степенной функции справедливы равенства
,
выделенная в плоскости с разрезом вдоль
отрицательной полуоси, называется
главной ветвью степенной функции. В
силу теоремы о производной сложной
функции для каждой регулярной ветви
степенной функции справедливы равенства
![]() ,
,
где f (z) — регулярная ветвь логарифмической функции Ln z. Мы получили обычную формулу для производной степенной функции:
![]() .
.
2. Перейдем к тригонометрическим функциям. Для действительных значений х из формулы Эйлера следует, что
еiх = cos х + i sin x, е- iх = cos x — i sin x.
Отсюда
cos x =
![]() ,
sin x =
,
sin x =![]() .Эти
формулы служат основой следующего
определения.
.Эти
формулы служат основой следующего
определения.
Тригонометрические функции комплексного переменного z определяются равенствами
![]() ,
,![]() ,
,![]() ,
,![]() .(26)
Определенные таким образом функции
сохраняют многие свойства тригонометрических
функций действительного переменного.
Из периодичности функции ez
следует, что функции sin z и cos z периодичны
с периодом 2
π,
a tg z и ctg z — с периодом π.
Функция sin
z
нечетна, a cos z — четна. Действительно,
.(26)
Определенные таким образом функции
сохраняют многие свойства тригонометрических
функций действительного переменного.
Из периодичности функции ez
следует, что функции sin z и cos z периодичны
с периодом 2
π,
a tg z и ctg z — с периодом π.
Функция sin
z
нечетна, a cos z — четна. Действительно,
![]() .
Аналогично доказывается четность
функции cos z. Для функций, определенных
равенствами (26), справедливы обычные
тригонометрические соотношения.
Например,
.
Аналогично доказывается четность
функции cos z. Для функций, определенных
равенствами (26), справедливы обычные
тригонометрические соотношения.
Например,
sin2 z + cos2 z = 1, sin(z1 + z2) = sin z1 cos z2 + cos z1 sin z2 и т.д. Все эти соотношения вытекают из (26).
Функции sin z и cos z аналитичны во всей плоскости С, причем имеют место обычные формулы дифференцирования:
(sin z) ' = cos z, (cos z) ' = - sin z.
Докажем,
например, формулу для производной sinz:
![]() Используя
формулы для производной частного,
получим
Используя
формулы для производной частного,
получим
![]() ,
,![]() .
.
Однако не все свойства тригонометрических функций действительного переменного сохраняются при продолжении этих функций в комплексную плоскость. В частности, sinz и cosz могут принимать значения, по модулю превосходящие 1. Например,
![]() ;
;![]() .
.
3. Функции, обратные (26), называются обратными тригонометрическими функциями. Так как тригонометрические функции (26) периодичны, то обратные к ним функции будут бесконечнозначными. В силу того что функции (26) достаточно просто выражаются через показательные, обратные к ним функции удается выразить через логарифмы. Получим такое выражение, например, для w = Arccos z. Из определения этой функции имеем
z
= cos
w
=
![]() ,
откуда e2
iw
— 2ze iw
+ 1 = 0. Решая это квадратное уравнение
относительно e iw,
находим
,
откуда e2
iw
— 2ze iw
+ 1 = 0. Решая это квадратное уравнение
относительно e iw,
находим
![]() (мы опускаем ± перед знаком квадратного
корня, поскольку понимаем корень как
двузначную функцию, принимающую оба
соответствующих значения). Из последнего
равенства получаем
(мы опускаем ± перед знаком квадратного
корня, поскольку понимаем корень как
двузначную функцию, принимающую оба
соответствующих значения). Из последнего
равенства получаем
![]() .
.
В
силу соотношения
![]() изменение знака перед корнем приводит
к изменению знака перед логарифмом. Но
корень принимает значения как с "+"
так и с "—". Значит, и среди значений
Arccos z будут значения как с "+", так
и с " —" перед логарифмом. Поэтому
знак "—" можно не писать:
изменение знака перед корнем приводит
к изменению знака перед логарифмом. Но
корень принимает значения как с "+"
так и с "—". Значит, и среди значений
Arccos z будут значения как с "+", так
и с " —" перед логарифмом. Поэтому
знак "—" можно не писать:
![]() (27)
(27)
Аналогичные формулы можно дать и для других обратных тригонометрических функций:
![]()
![]() (28)
(28)
Из элементарных функций комплексного переменного отметим также гиперболические функции sh z, ch z, th z, и cth z, определяемые равенствами
![]() ,
,![]() ,
,
![]() ,
,![]() ,
(29)
,
(29)
Они весьма просто выражаются через тригонометрические функции:
sh z = — i sin iz, ch z = cos iz, th z = — i tg iz, cth z = i ctg iz,
и поэтому несущественно отличаются от последних.
4. Функцией Жуковского называется функция
![]() . (30)
. (30)
Эта
функция имеет важные применения в теории
крыла самолета, а также весьма полезна
при построении ряда конформных
отображений. Она аналитична всюду в
![]() ,
кроме точекz
= 0 и z
= ∞.
Производная
,
кроме точекz
= 0 и z
= ∞.
Производная
![]()
существует
всюду в
![]() ,
за исключением точекz
= 0 и z
= ∞,
и обращается в нуль при z
= ±1. Поэтому отображение (30) конформно
всюду, кроме точек 0, ±1
,∞.
,
за исключением точекz
= 0 и z
= ∞,
и обращается в нуль при z
= ±1. Поэтому отображение (30) конформно
всюду, кроме точек 0, ±1
,∞.
Выясним,
при каком условии две различные точки
переходят в одну и ту же точку. Пусть z1
≠
z2
и
![]() .
.
Отсюда
следует, что
![]() .
.
Так как z1 ≠ z2, то это равенство равносильно условию zlz2 = 1. (31)
Поэтому для однолистности функции Жуковского в некоторой области D необходимо и достаточно, чтобы эта область не содержала пары различных точек, удовлетворяющих условию (31). Такими областями являются, например, внешность |z| > 1 единичного круга (при этом |z1z2| > 1) и внутренность |z| < 1 этого круга (|z1z2| < 1).
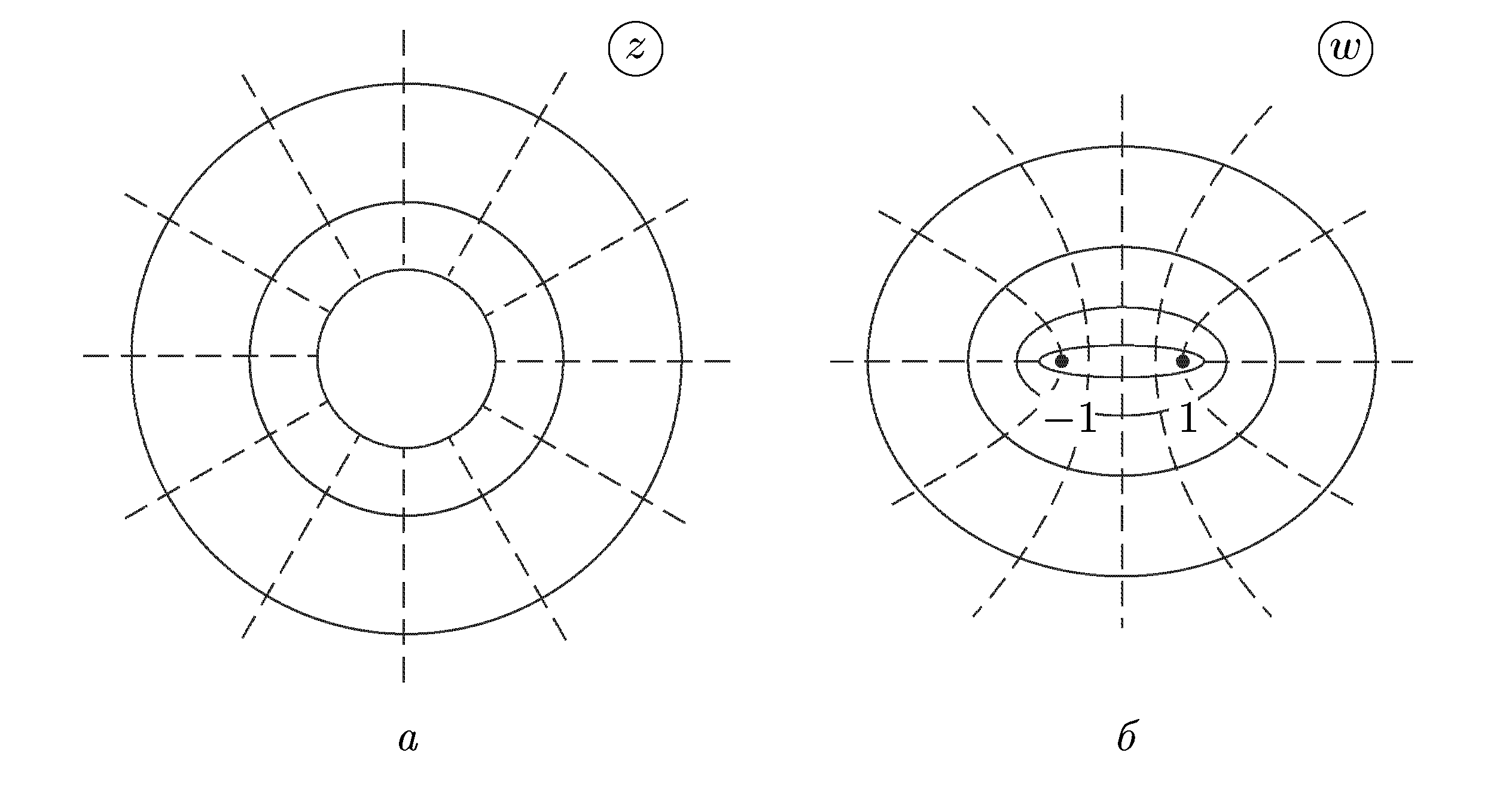
Чтобы
наглядно представить себе отображение
(30), выясним, в какие кривые оно переводит
окружности (показаны на рис. 9а сплошными
линиями) и лучи (показаны пунктирами).
Положим z
=![]() .
Тогда (30) перепишется в виде
.
Тогда (30) перепишется в виде![]() ,
откуда
,
откуда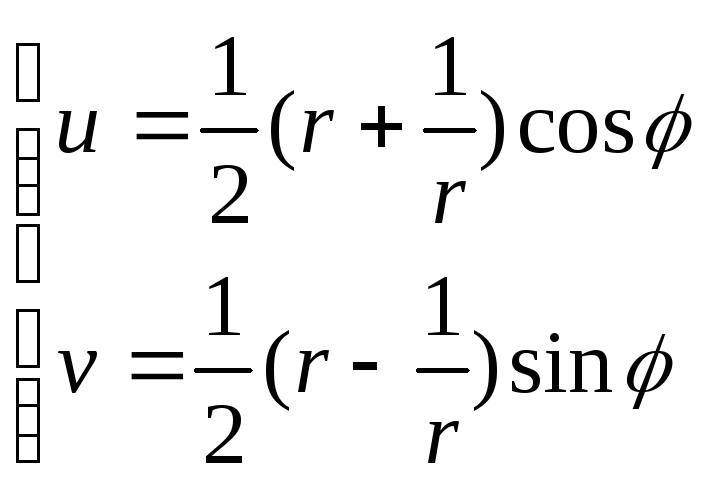 (32)
(32)
Рассмотрим образы окружностей r = r0. Из (32) следует
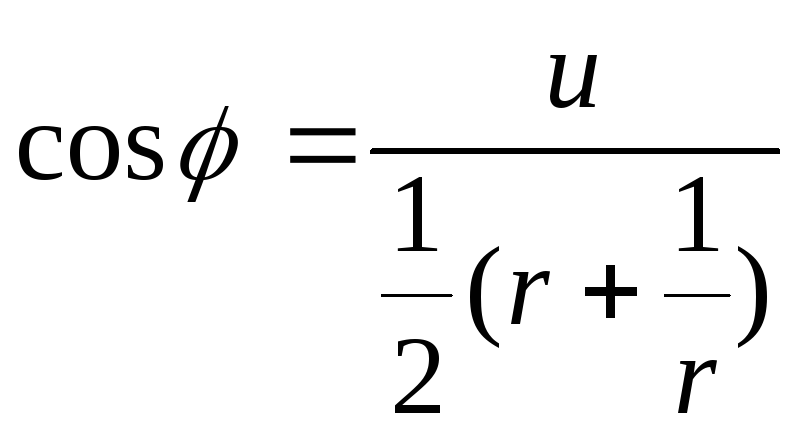 ,
,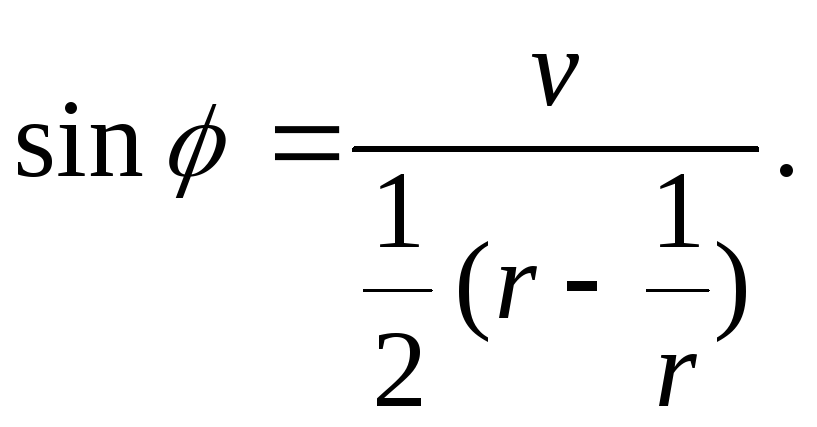
 (рис.
9)
(рис.
9)
Возводя эти равенства в квадрат, складывая и полагая r = r0, получим
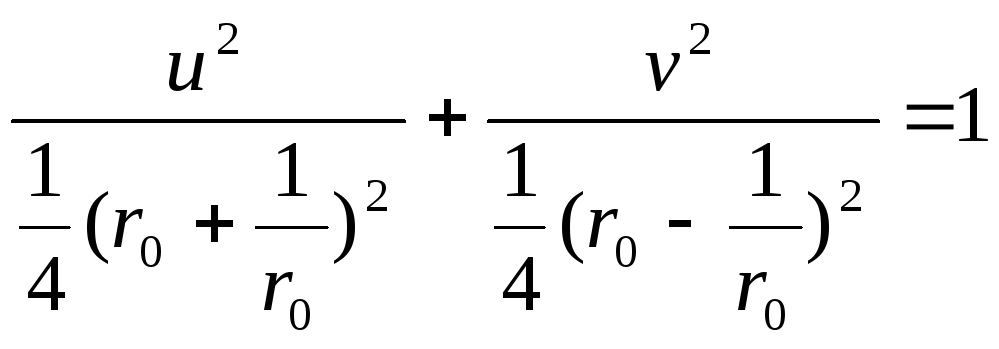 (33)
(33)
Уравнение (33) является уравнением эллипса с полуосями
![]()
Итак,
образами окружностей |z|
= r0
в плоскости z
будут эллипсы в плоскости w
(рис. 9б). Если r0
→
1, то a
r
0
→
1, b
r
0
→
0. Поэтому эллипсы будут стягиваться к
отрезку [—1,1]. При больших r0
разность a
r
0
— b
r
0
=
![]() мала, и эллипсы мало отличаются от
окружностей.
мала, и эллипсы мало отличаются от
окружностей.
Чтобы
получить образ лучей
![]() ,
преобразуем равенства (32) к виду
,
преобразуем равенства (32) к виду
![]()
Возводя
эти равенства в квадрат, вычитая из
первого второе и полагая
![]() ,
получим
,
получим![]() (34)
(34)
Уравнение
(34) является уравнением гиперболы с
полуосями
![]() ,
,![]() .
Следовательно, лучи
.
Следовательно, лучи![]() отображаются в части гипербол (рис. 9б).
отображаются в части гипербол (рис. 9б).
Таким образом, функция Жуковского взаимно-однозначно и конформно отображает внешность единичного круга на внешность отрезка [-1,1].
Из (30) легко видеть, что w(z) = w(l/z). Функция w = 1/z взаимно-однозначно и конформно отображает внутренность круга |z| < 1 на внешность этого же круга. Отсюда следует, что функция Жуковского взаимно-однозначно и конформно отображает также и внутренность единичного круга на внешность отрезка [—1,1].
Список литературы.
