Определение двойного интеграла

Рассмотрим на плоскости Оху область D площади S, ограниченную замкнутой кривой  (рис. 6). Пусть в области D определена функция z = f(x, y). Разобьем область D произвольным образом на п элементарных областей D₁, D₂, …, D_n, имеющих площади S₁, S₂, …, S_n и диаметры d₁, d₂, …, d_n (рис. 7). В каждой i-й элементарной области D_i выберем произвольную точку M_i(x_i, y_i), значение функции в этой точке f(x_i, y_i) умножим на площадь S_i соответствующей области и все произведения сложим. Полученная сумма

называется интегральной суммой функции f(x, y) в области D.

Если при интегральная сумма имеет определенный конечный предел

, (1)

не зависящий от способа разбиения D на элементарные области и от выбора точек M_i(x_i, y_i) в пределах каждой из них, то этот предел называется двойным интегралом от функции f(x, y) в области D.

у

у



D_i

D



0 х

0 х

Рис. 6

Рис. 7

Двойной интеграл обозначается одним из символов:

;

.

Функция z = f(x, y), для которой предел (1) существует и конечен, называется интегрируемой. Если функция z = f(x, y) непрерывна в области D, то она является интегрируемой в этой области.

Геометрический смысл двойного интеграла. Если f(x, y) > 0 в области D, то двойной интеграл равен объему цилиндрического тела, ограниченного сверху поверхностьюz = f(x, y), с боков – цилиндрической поверхностью, образующие которой параллельны оси Oz, а направляющей служит граница  области D, снизу – плоскостью z = 0.

Физический смысл двойного интеграла. Двойной интеграл от функции z = f(x, y) > 0 по области D представляет собой массу пластины D, если подынтегральную функцию f(x, y) считать плотностью этой пластины в точке М(х, у).

Свойства двойного интеграла:

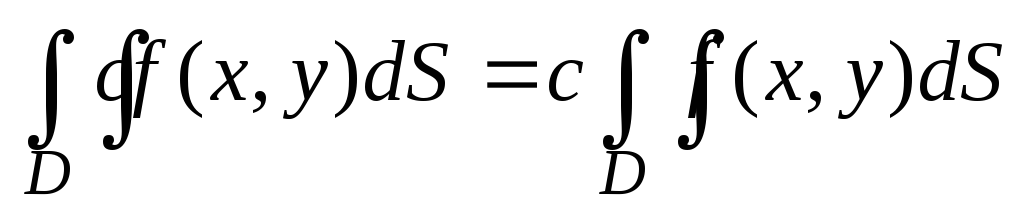1. , где с – постоянная.

2. .

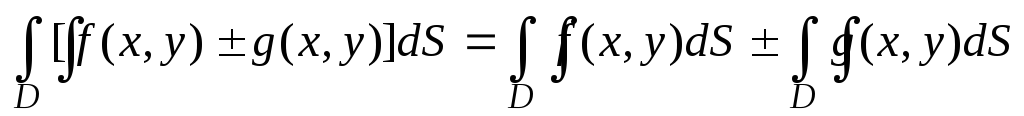3. Если f(x, y)  g(x, y), то .

4. .

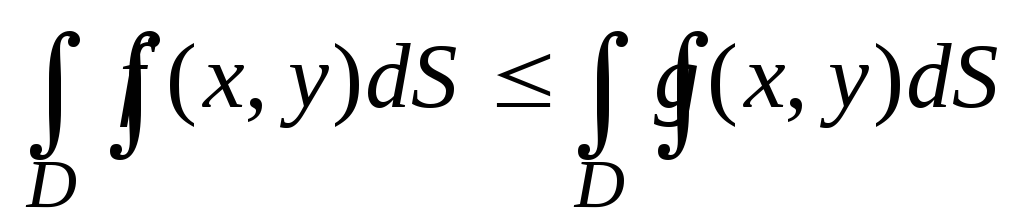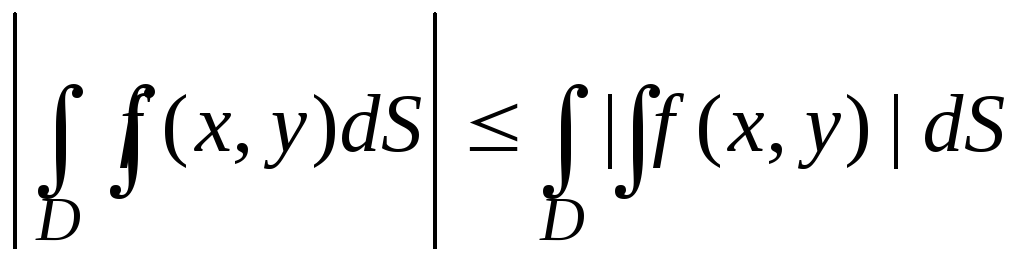5. Если область интегрирования D разбита на две области D₁ и D₂, то

.

6. Оценка двойного интеграла. Если 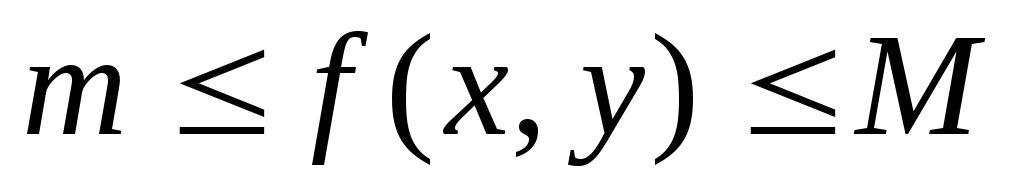, то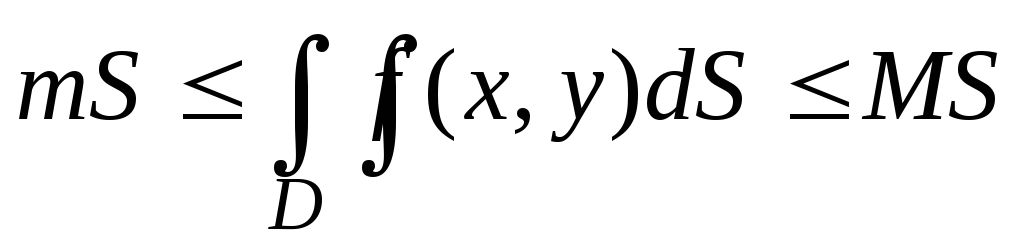, гдеS – площадь области D, а т и М – соответственно наименьшее и наибольшее значения функции f(x, y) в области D.

Приведение двойного интеграла к повторному в случае прямоугольной области

Пусть область D является прямоугольником со сторонами, параллельными осям координат (рис. 8). Обозначим его так:

y

d

c

, т.е. a  x  b, с  у  d.

0 a b x

Рис. 8

Если для функции f(x, y), определенной в прямоугольнике , существует двойной интеграл

, (2)

а при каждом фиксированном значении х из [a, b] – простой интеграл

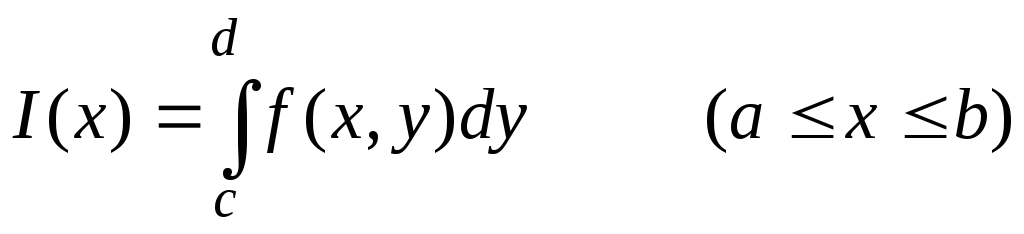, (3)

то существует также повторный (или двукратный) интеграл

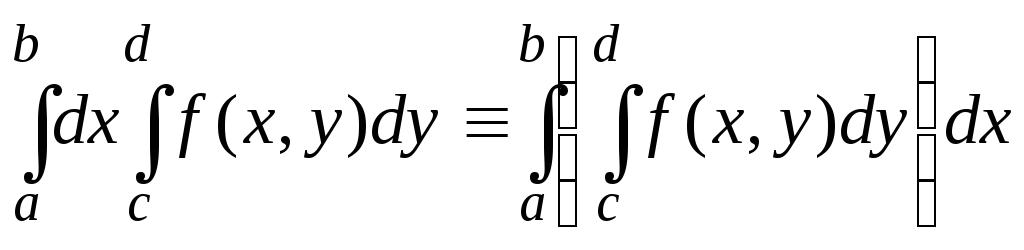, (4)

причем выполняется равенство

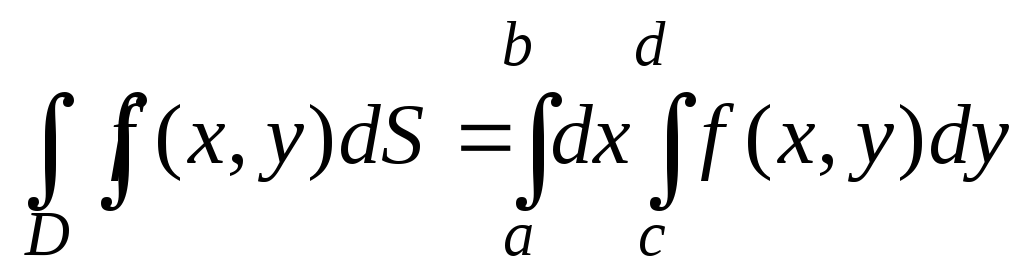. (5)

Если существует двойной интеграл (2), а при каждом постоянном значении у из [c, d] – простой интеграл

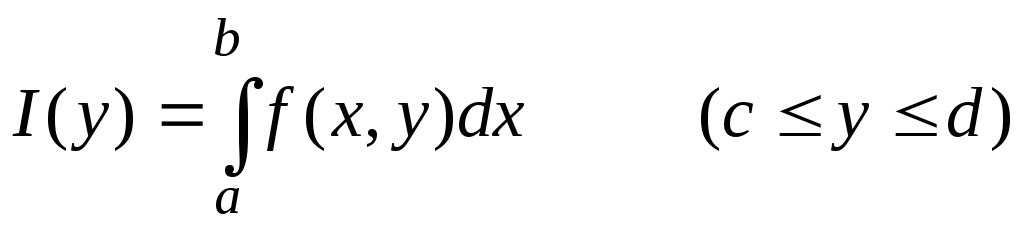, (6)

то существует также повторный интеграл

, (7)

причем

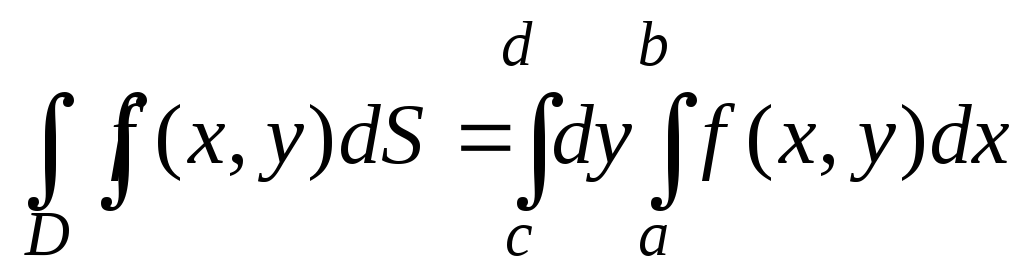. (8)

Если вместе с двойным интегралом (2) существуют оба простых интеграла (3) и (6), то выполняются одновременно равенства (5) и (8), откуда

.

Пример 1. Вычислить повторный интеграл .

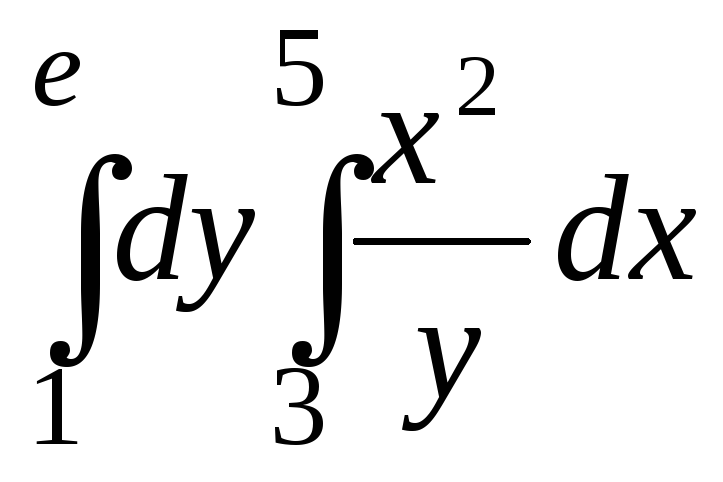В соответствии с формулой (7)

.

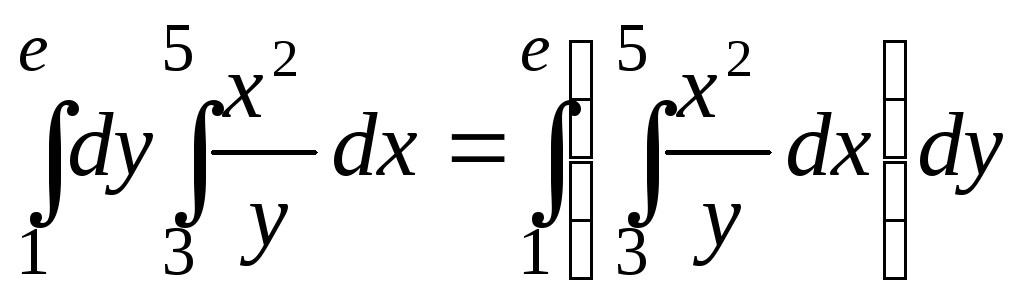Вычислим сначала интеграл, стоящий в скобках (он называется внутренним интегралом). Считая у постоянным, находим

.

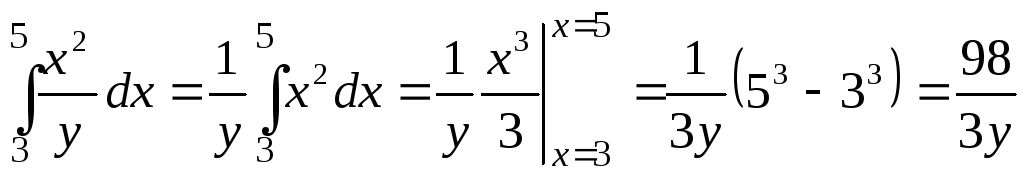Вычисляем внешний интеграл, для чего полученную функцию интегрируем по у в пределах от 1 до е:

.

Пример 2. Вычислить повторный интеграл .

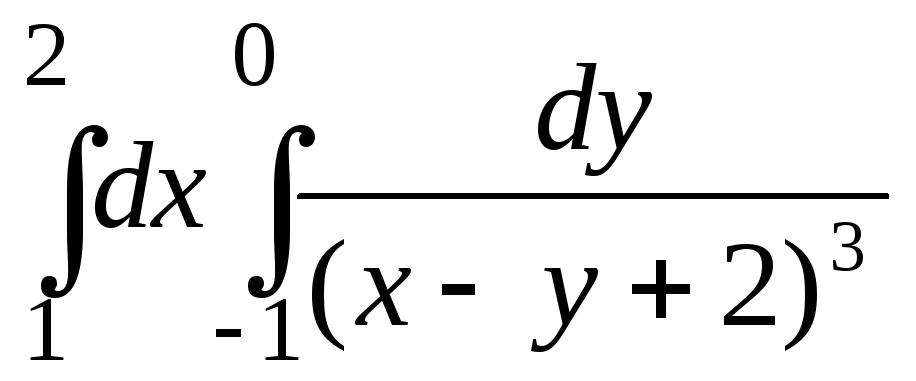В соответствии с формулой (4)

.

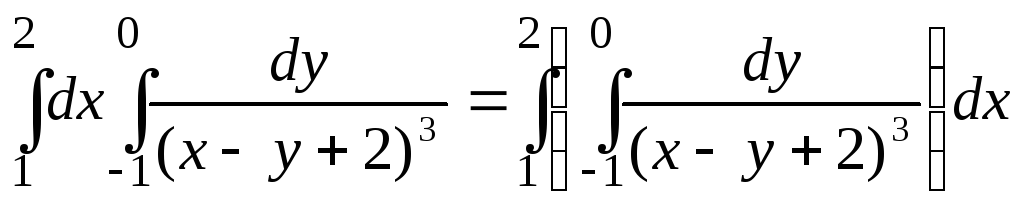Вычисляем внутренний интеграл, считая х постоянным:

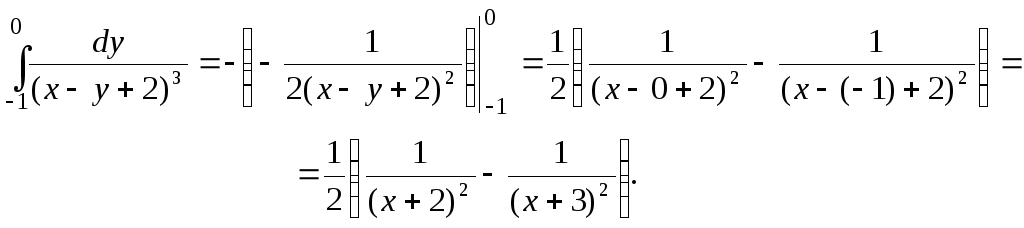
Полученную функцию проинтегрируем по х в пределах от 1 до 2:

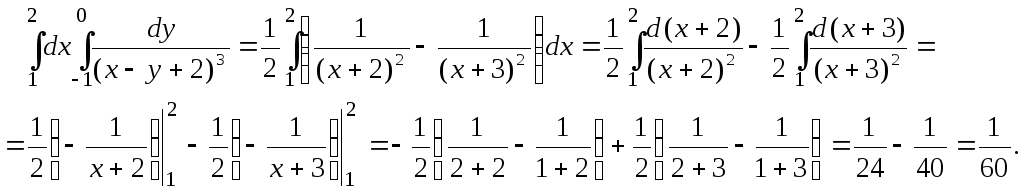
Пример 3. Вычислить повторный интеграл .

Не выписывая отдельно вычисление внутреннего интеграла, находим

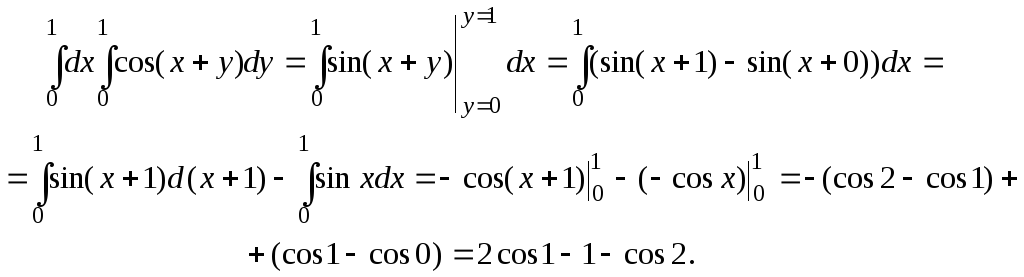
Пример 4. Вычислить , где областьD является прямоугольником [2, 4; 1, 3].

Задача сводится к вычислению повторного интеграла с помощью формулы (5). По этой формуле интегрирование выполняется сначала по у в пределах от с до d при произвольном постоянном х, а потом – по х в пределах от а до b. Формула (5) в данном случае примет вид

.

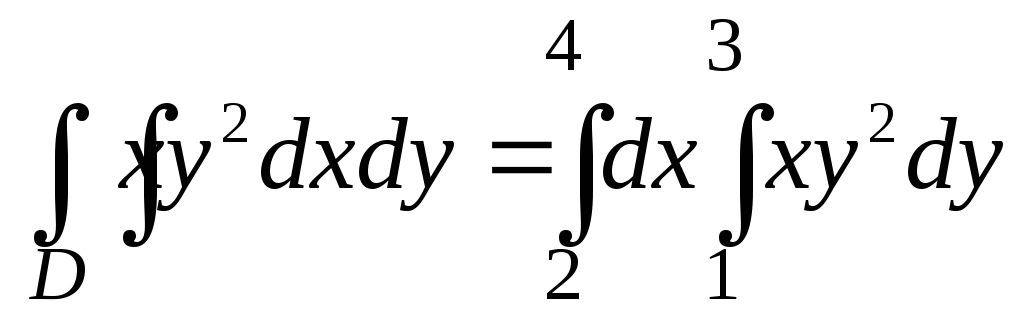Так как

,

то

.

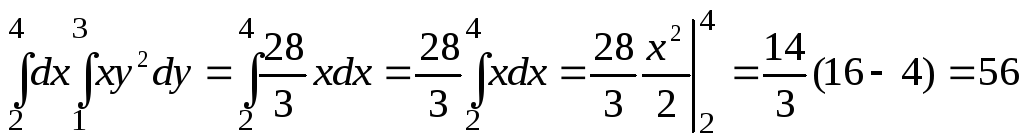Следовательно,

.

Замечание. Тот же результат можно получить и по формуле (8):

.

Действительно,

,

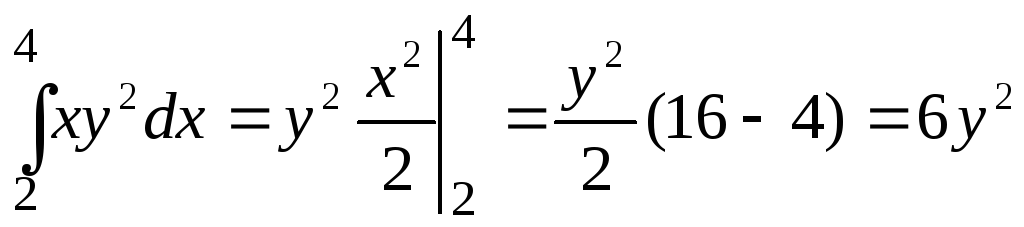поэтому

.

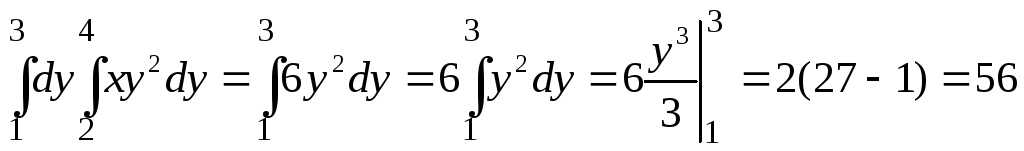Пример 5. Вычислить , гдеD - прямоугольником [1, 2; 0, 3].

Подынтегральная функция представляет собой произведение функции только от х на функцию только от у, т.е.

,

где ,, поэтому при вычислении двойного интеграла можно пользоваться формулой вида

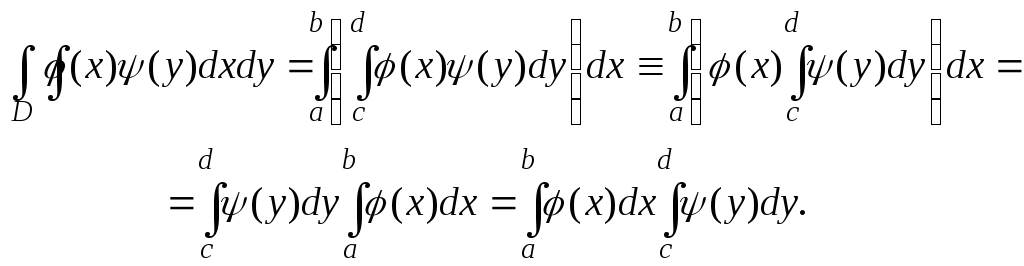
Следовательно,

.

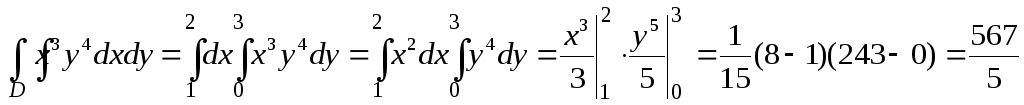Пример 6. Вычислить , гдеD - квадрат .

Не выписывая отдельно вычисление внутреннего интеграла, находим

.
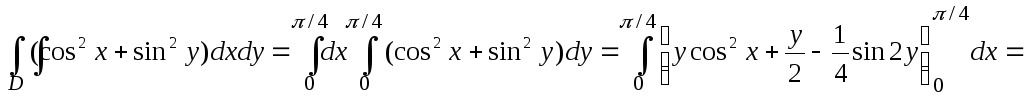
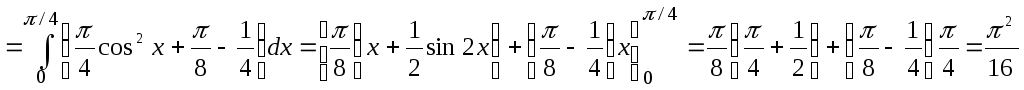