2. Простейшие операции над векторами

К простейшим операциям над векторами относится сложение и вычитание векторов и умножение вектора на скаляр. Все эти операции называются линейными.

1) Сложение векторов.

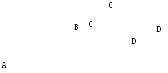
Определение 1. Чтобы найти сумму двух векторов и, необходимо конец векторасовместить с началом. Вектор, соединяющий точкии, будет их суммой.

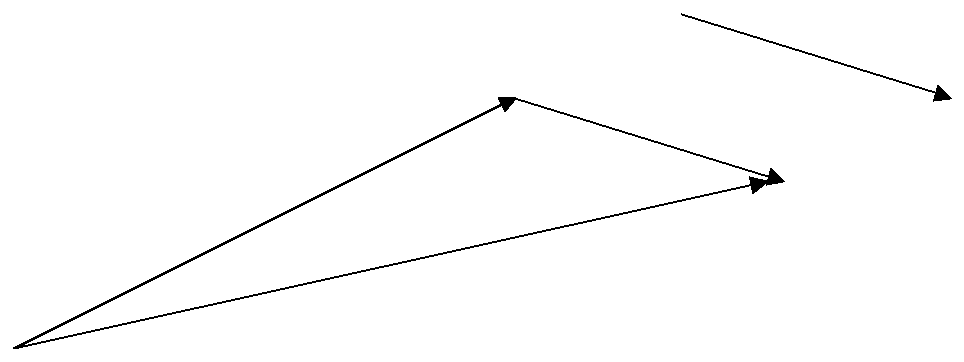
Обозначается сума следующим образом: . Величину ее можно найти и другим способом. Начала векторовисовмещаются и на них как на сторонах строится параллелограмм. Диагональ параллелограмма и будет суммой векторов.

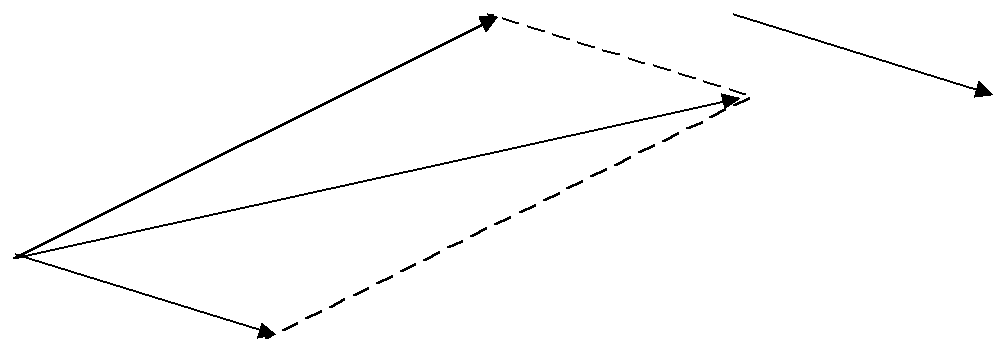
Из правила параллелограмма видно, что сумма векторов обладает переместительным свойством

.

Если слагаемых больше, например, три: , поступают следующим образом. Строят вначале сумму, а затем, прибавляя, получают вектор.

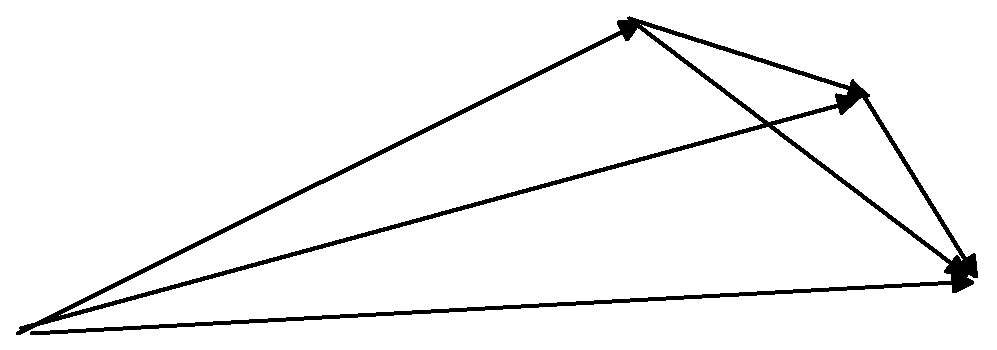
Из рисунка видно, что тот же результат будет, если сложить вначале , а затем прибавить, то есть сумма векторов обладает сочетательным свойством:

.

Если при сложении нескольких векторов конец последнего совпадает с началом первого, то сумма равна ноль вектору . Очевидно,.

2) Разность векторов.

Определение 2. Разностью двух векторов иназывается такой вектор, сумма которого с вычитаемымдает вектор.

Значит, если , то.

Из определения суммы двух векторов вытекает правило построения разности. Откладываем из общей точки векторы и. Векторсоединяет концы векторовии направлен от вычитаемого к уменьшаемому.

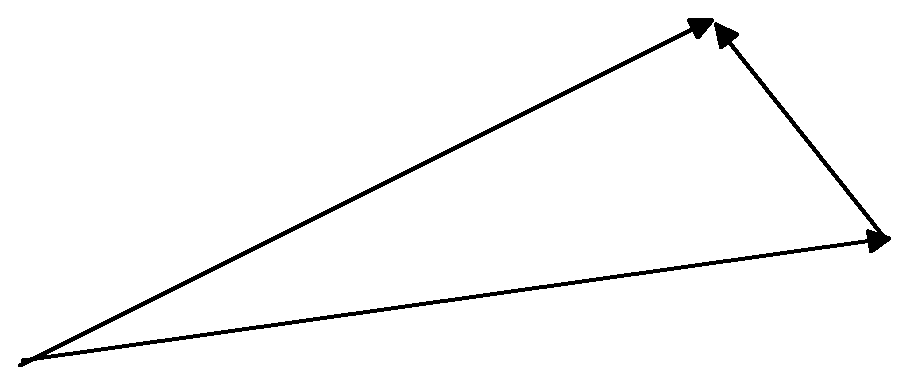
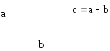
Видно, что если на векторах ипостроить параллелограмм, то одна его диагональ соответствует их сумме, а вторая - разности.

3) Умножение вектора на число.

Определение 3. Произведением вектора на числоназывается вектор, определенный следующими условиями:

1) ;

2) вектор коллинеарен вектору;

3) векторы инаправлены одинаково, если, и противоположно, если.

Очевидно, что операция умножения вектора на число приводит к его растяжению или сжатию. Противоположный вектор можно рассматривать как результат умножения векторана. Отсюда,.

Из определения 3 следует, что если , то векторыиколлинеарны. Отсюда вытекает определение коллинеарности векторов.

Определение 4. Любые два вектора иколлинеарны, если связаны соотношением, где- некоторое число.

Величину можно определить из отношения. Оно положительно, если векторы направлены в одну сторону, и наоборот отрицательно, если направление векторов противоположно.

Из построения параллелограмма легко убедиться, что умножение вектора на число обладает распределительным свойством:

;

и сочетательным свойством

.

Определение 5. Вектор, длина которого равна единице, называется единичным вектором или ортом.

Обозначаются единичные векторы символами или.

Используя понятие единичного вектора, любой вектор можно представить следующим образом: .

Числовые матрицы.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел и допускающий алгебраические операции (сложение, вычитание, умножение) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицами. Иногда рассматривают многомерные матрицы или матрицы непрямоугольной формы. Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]» или двойными прямыми линиями "||…||"). Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной (к примеру a₁₁ является элементом матрицы А). У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размера », подразумевая, что в матрице m строк и n столбцов. В одной матрице всегда ,

История

Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрасссу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.

Операции над матрицами

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

c_ij = a_ij + b_ij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

c_ij = a_ij - b_ij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

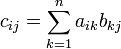
В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть .

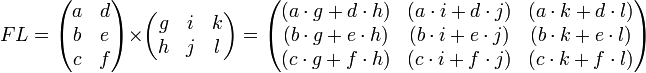
Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A — матрица размера , то A^T — матрица размера

Свойства операций над матрицами

Ассоциативность сложения: A + (B + C) = (A + B) + C.

Коммутативность сложения: A + B = B + A.

Дистрибутивность умножения относительно сложения:

A(B + C) = AB + AC;

(B + C)A = BA + CA.

Свойства операции транспонирования матриц:

(A^T)^T = A

(AB)^T = B^TA^T

(A ^{− 1})^T = (A^T) ^{− 1}, если обратная матрица A ^{- 1} существует.

Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

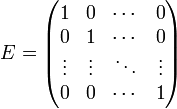
Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A ^{- 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

AA ^{− 1} = E

Общее определение абстрактного векторного пространства.

V ≠ ;a, b, c є V; P-числовое поле.

Пусть: 1. Задана операция ∆, которая каждому a є V и каждому λ є P ставит в соответствие элемент λ∆a є V.

2. ∀ a,b є V задана операция □, которая каждой упорядоченной паре a,b є V ставит в соответствие единственный элемент a□b є V.

При этом выполняются 8 свойств (аксиом).

1.  a□(b□c)=(a□b)□c

2. Ǝ z є V | ∀ a є V |a□z=z□a=a

3. ∀ a Ǝ n | n□a=a□n=z

4. a□b=b□a

5. (α+β)∆a=(α∆a)□(β∆a)

6. α∆(a□b)= (α∆a)□(α∆ b)

7. α∆(β∆a)= (αβ)∆a

8.1∆a=a

∀ a, b є V; α,β є P; 1 є P

Тогда множество V называется векторным пространством над полем Р, операция □=+, ∆=умножение вектора на число, z-единичный элемент=0, а его элементы-векторы.

Перестановки и подстановки из n символов.

Перестановкой чисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12...n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.

Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.

Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ 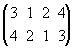 обозначает подстановку, в которой 3 переходит в 4, 1  2, 2  1, 4  3. Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). 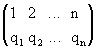Всякая подстановка n-ой степени может быть записана в виде ,т.е. с натуральным расположением чисел в верхней строке.

Пусть нам дана квадратная матрица порядка n

                                    .                                                 

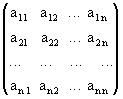Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:

                        ,                                                   

где индексы q₁, q₂,..., q_n составляют некоторую перестановку из чисел 1, 2,..., n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения равен (- 1)^q, где q - число инверсий в перестановке вторых индексов элементов.