1.2. Числовые множества.

В процессе изучения математики вводятся уже в средней школе следующие числовые множества.

а) N = {1, 2, 3, … , n, …} - множество натуральных чисел.

б) Z = {0, ±1, ±2, … , ±n, …} - множество целых чисел.

в) Q = | - множество рациональных чисел, т.е. множество всевозможных обыкновенных дробей (n0).

г) R – множество действительных (вещественных) чисел, т.е., грубо говоря, таких чисел, каждое из которых с любой степенью точности может быть приближенно (заменено) рациональным числом. Иначе говоря, R – множество всевозможных десятичных дробей, как конечных, так и бесконечных. При этом всякая обык-новенная дробь (т.е. рациональное число) представляется либо конечной дробью, либо бесконечной периодической дробью. Вся-кая бесконечная непериодическая десятичная дробь называется иррациональным числом.

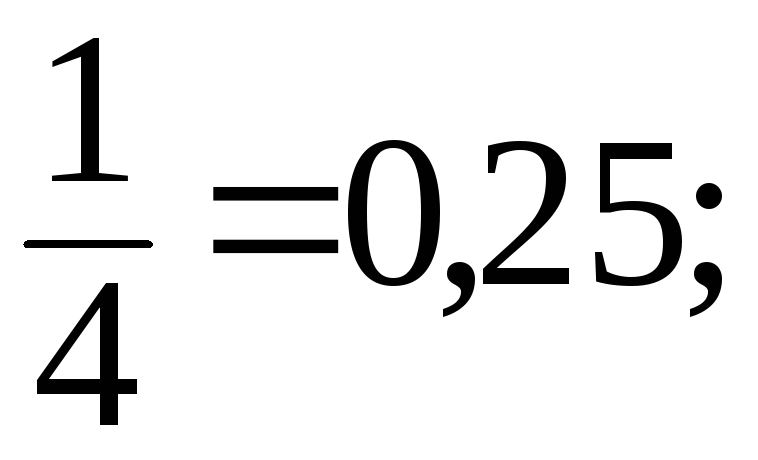
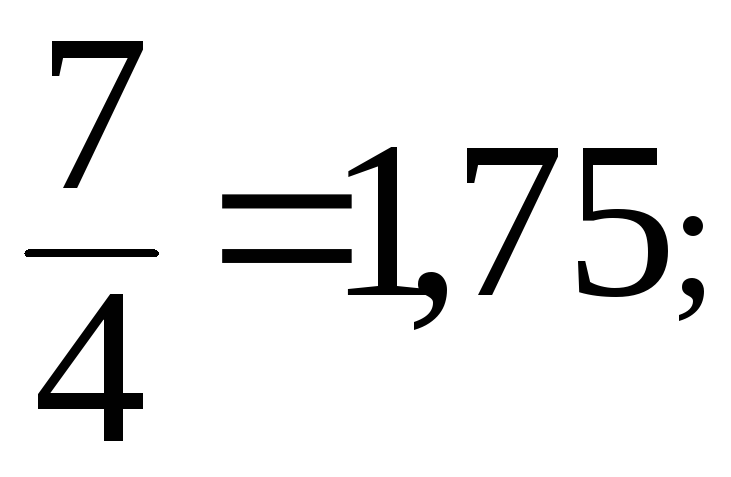
Например, числа 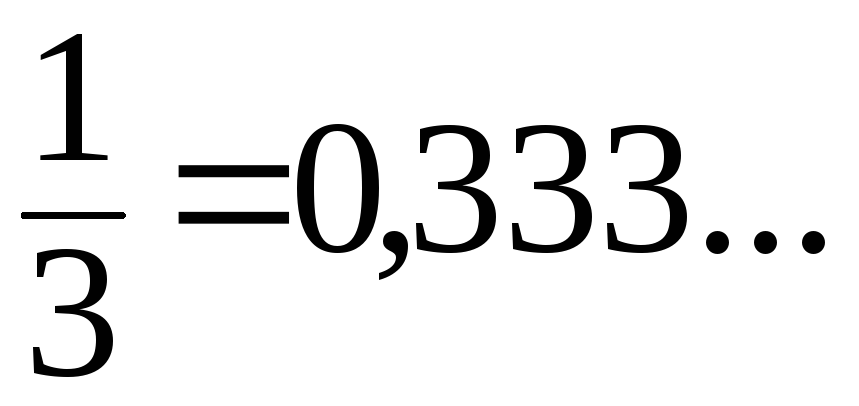(три в периоде) являются рациональными. Числоявляется ирра-циональным. Это, правда, требует отдельного доказательства.

Оказывается, что между любыми двумя различными действи-тельными числами всегда имеется бесконечное множество как рациональных, так и иррациональных чисел.

д) [а, b], [а, b), (а, b], (а, b), [а, +∞), (-∞, b], (а, +∞), (-∞, b) – интервалы (отрезки, промежутки) числовой прямой (т.е. множества действительных чисел) R, которые состоят из чисел , удовлетворяющих, соответственно, неравенствам:а ≤ х ≤ b, а ≤ х <b, а < х ≤ b, а < х < b, а ≤ х < +∞, -∞ < х ≤ b, а < х < +∞, -∞ < х < b. В этих обозначениях обычно предполагается, что а < b.

е) Для любой точки (числа) и любого числаопределено множество – интервал (а – δ, а + δ), симметричный относительно точки а. Этот интервал называется δ-окрестностью точки а, а δ – её радиусом. Эта окрестность определяется неравенствами:

или

Т.о. точка тогда и только тогда, когдах удовлетворяет указанным неравенствам.

1.3. Отображения

Говорят, что задано отображение одного множества Х (≠ Ø) в другое множество Y, если каждому элементу (точке) по неко-торому правилуf поставлен в соответствие единственный элемент (точка) . Иначе говоря,отображение – это тройка (Х, f, Y), в которой Х и Y – множества, а f – указанное выше правило.

Для обозначения отображения используются также записи:

или

(читается одинаково: отображение «эф» множества «икс» во мно-жество «игрек»), или, подробнее:

(читается: отображение f множества Х во множество Y, переводя-щее точку в точку. При этом пишут:y = f(x), ,; точкуу называют образом точки х , а х – прообразом точки у (при отображении f); Х называют множеством определения отображения f, а Y – множеством изменения (значений - образов) отображения f.

В случае, когда Y – числовое множество, отображение часто называютфункцией (на множестве Х).

Иногда, множество Х называют областью определения, а Y множеством значений функции Это словоупотребление нельзя признать корректным. Во-первых, термин «область» не является вакантным; он употребляется в курсе высшей математики совсем в другом смысле в интегральном исчислении Во-вторых, множество Y правильнее называть именно множеством изменения, а не множеством значений отображения (функции) т.к. множество значений – это образ f(Х) множества Х при отображении ; в общем случаеf(Х) не совпадает с Y.

Приведём некоторые примеры.

1. Х – множество студентов в аудитории, Y – множество стуль-ев в этой же аудитории. Отображение (правило) f заключается в следующем: каждому студенту (точке) ставится в соответ-ствие тот единственный стул (точка), на котором сидитх. Имеется отображение

.

2. Х – множество студентов в аудитории. Y=R – множество действительных чисел. Каждое из следующих словосочетаний определяет некоторую функцию: «рост студента», «вес студента», «размер обуви студента» и т.д.

Отображение называется:

1. взаимно однозначным «в» (или инъективным), если образы любых двух различных точек различны;

2. отображением «на» (или сюръективным), если для любого 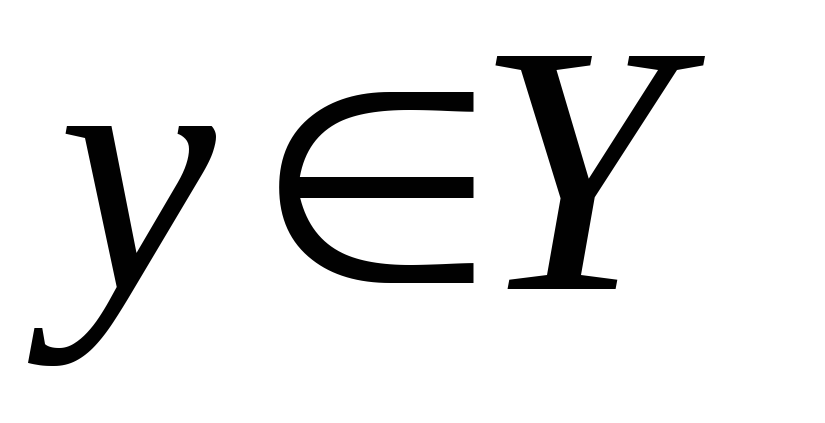, существует хотя бы один прообраз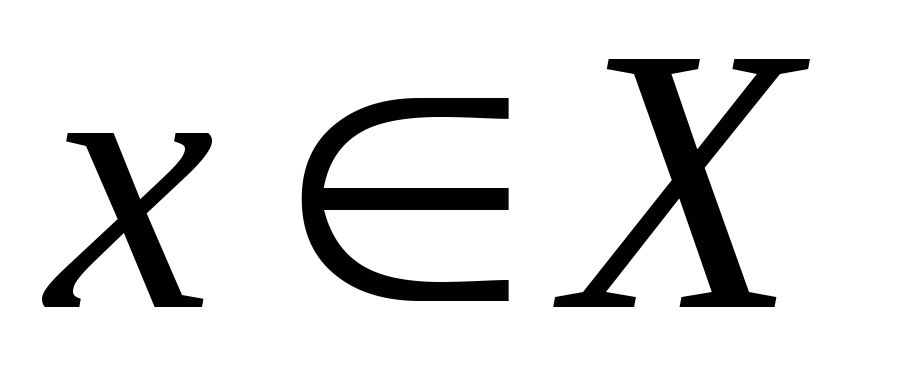, т.е. такая точках, образ которой ;

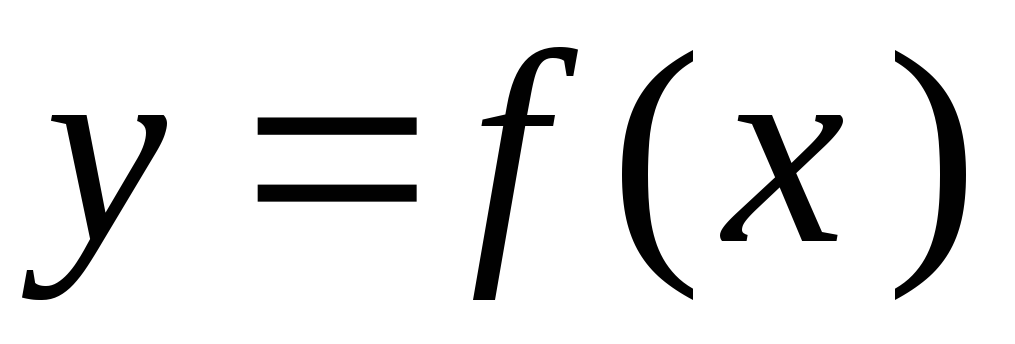3. взаимно однозначным (или биективным), если оно обладает первыми двумя свойствами одновременно.

Эти свойства отображений можно проиллюстрировать с по-мощью только что приведённых примеров. Так отображение при-мера 1 является – по смыслу инъективным (разные студенты сидят на разных стульях); оно будет сюръективным, если нет свободных стульев; в этом случае оно будет и взаимно однозначным (биек-тивным).

В примере 2 отображение «рост студента», например, будет инъективным, если в аудитории нет студентов одинакового роста. В противном случае, оно не является инъективным. Эта же функция «рост студента» не может быть сюрьективной, ибо – в противном случае – в аудитории были бы студенты любого наперёд заданного (в том числе, отрицательного) роста.