3Линейка / Задачник-2 / Ответы и указания (2)
.docОтветы и указания
7.1.1. Нулевую.
7.1.2.
7.1.3.
7.1.5. а) Да; б) нет.
7.1.6.
а)
линейно,
б),
в)
не является линейным;
г)
линейно,
7.1.7.
а)
б)
Указание. Воспользуйтесь формулой
бинома Ньютона.
в)
г)
Указание. Воспользуйтесь формулой
бинома Ньютона.
7.1.8.
7.1.9.
7.1.10.
7.1.11.
не изменится.
7.2.1.
а)
- образ
,
- прообраз
б)
- образ
,
- прообраз
в)
- образ
,
- прообраз
7.2.2.
а)
б)
в)
7.2.3.
а)
Да,
б)
нет, так как система
линейно зависима, а система
линейно независима;
в)
да,
7.2.4.
а)
Да,
б)
нет, так как система
линейно зависима, а система
линейно независима.
7.2.5.
а)
,
базис
-
,
базис
-
б)
,
базис
-
,
базис
-
в)
,
.
7.2.6.
Образ -
,
ядро -
.
7.2.7.
.
7.2.8.
.
7.2.9.
а)
Например, базис
-
,
базис
-
б)
в)
например, базис
-
базис
-
7.2.10.
.
7.3.1.
.
7.3.2.
.
7.3.3.
.
7.3.4.
.
7.3.5.
В матрице переставляется
- я и
- я строки и
- й и
- й столбцы.
7.3.6.
а)
б)
.
7.3.7.
а)
;
б)
;
в)
.
7.3.8.
.
7.3.9.
.
7.3.10.
а)
б)
в)
.
7.3.11.
а)
б)
в)
.
7.4.3.
Собственными значениями являются
диагональные элементы
.
7.4.6.
Указание. См. §
10 гл. II
в
.
7.4.12.
Если
- собственное значение оператора
,
то
- собственное значение оператора
.
7.4.13.
в)
Если
- собственное значение оператора
,
то
-
собственное значение оператора
.
7.4.14.
Если
- собственное значение оператора
,
то
- собственное значение оператора
.
7.4.15.
.
7.4.17.
.
7.4.19. а) Оператор проектирования имеет собственные значения 1 и 0;
при
этом
- собственное подпространство для
,
- собственное подпространство для
;
б) оператор отражения имеет собственные значения 1 и -1;
при
этом
- собственное подпространство для
,
- собственное подпространство для
.
7.4.21.
,
где
,
а
- собственные значения.
7.4.22.
Указание. Рассмотрите матрицу оператора
в базисе, первые векторы которого
образуют базис собственного подпространства,
соответствующего
.
С помощью этой матрицы вычислите
характеристический многочлен оператора.
Подробнее см. гл. 5, §
2, п. 5 книги
.
7.4.25.
а)
Над
:
;
над
:
;
б)
над
нет собственных векторов;
над
:
;
в)
над
:
;
;
над
:
;
;
г)
над
:
;
;
над
:
;
;
д)
над
:
;
;
над
:
;
;
е)
над
:
;
;
над
:
;
;
ж)
над
:
;
над
:
;
;
з)
над
:
;
над
:
;
;
и)
над
:
над
:
к)
над
:
;
над
:
;
л)
над
:
;
над
:
м)
над
:
;
;
над
:
;
.
7.5.6.
а)
б), в), е) матрицы к диагональному виду не приводятся;
г)
д)
.
7.5.7.
б),
в)
Да;
б)
в)
.
7.5.8.
а)
Да,
б) нет;
в) нет;
г)
да,
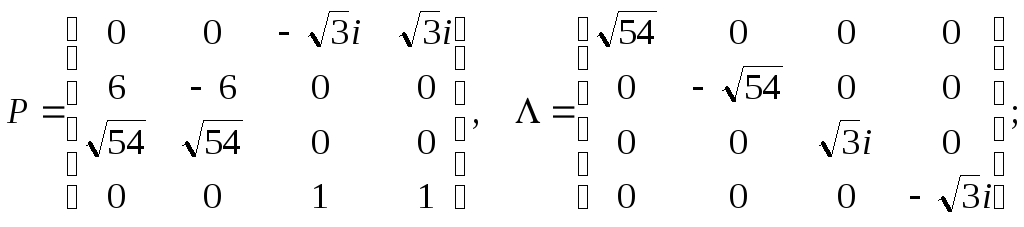
д)
да,
.
7.6.4.
Если
- диагональная матрица такая, что
,
то
,
где
- матрица, сопряженная к
.
7.6.5.
Всякий оператор одномерного пространства
есть умножение каждого вектора
пространства на фиксированное (для
данного оператора) число
.
Если пространство унитарное, то
сопряженный оператор есть умножение
на сопряженное число
.
В евклидовом одномерном пространстве
всякий оператор совпадает со своим
сопряженным.
7.6.6.
.
7.6.7.
.
7.6.8.
.
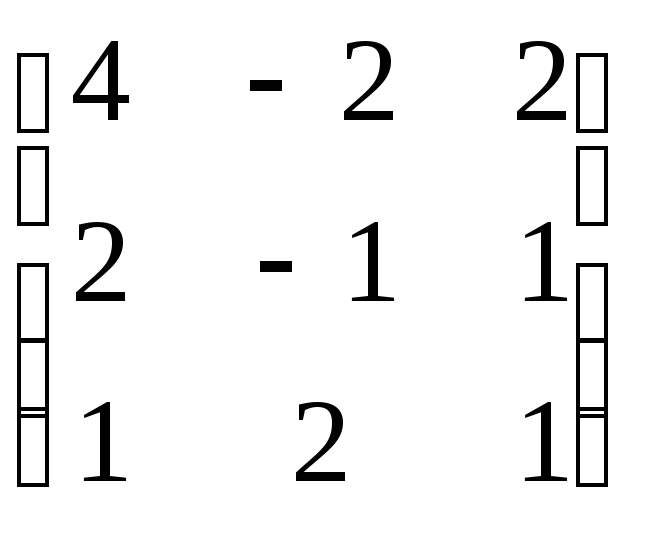7.6.9.
.
7.6.10.
.
7.6.11.
а)
б)
в)
.
-
а)
б)
в)
. -
а)
б)
в)
. -
Указание. Используйте соответствие между сопряженными операторами и сопряженными матрицами.
7.6.16.
а)
Базис ядра - многочлен
;
базис образа - многочлен
;
б)
базис ядра - многочлен
;
базис образа - многочлен
;
в)
базис ядра - многочлен
;
базис образа - многочлен
.
7.6.19.
Указание. Выберите
.
-
. -
а) Да; б) нет; в) да; г) да.
-
а) Да; б) нет.
7.6.32. а) Да; б) нет.
7.6.35. Базис составляют, например, векторы:
а)
б)
в)
.
-
Указание. Покажите, что
.
7.6.41. Нет, если собственные значения оператора простые; да, если хотя бы одно кратно.
-
. -
а)
б)
в)
г)
.
-
а)
б)
.
-
а)
б)
в)
г)
д)
е)
ж)
з)
.
-
Указание. См. решение задачи ? 1569 в
.
7.6.47.
а)
б)
.
7.6.48.
а)
б)
в)
.
7.6.49.
Указание.
См. §
7.2 в
.
Если, например, линейное преобразование
в ортонормированном базисе задано
матрицей
и вектор
задан координатами в том же базисе, то
.
7.6.50.
Указание. См. §
7.1. в
.