§ 7.6. Линейные операторы в унитарных и евклидовых пространствах

Линейный оператор , действующий в - мерном унитарном (евклидовом) пространстве , называется сопряженным к линейному оператору , если для любых векторов и из выполняется равенство

. (7.6.1)

В унитарном (евклидовом) пространстве каждому линейному оператору отвечает сопряженный оператор и притом только один.

Пусть - комплексная квадратная матрица порядка . Квадратная матрица порядка называется сопряженной к матрице , если для всех и

. (7.6.2)

В ортонормированном базисе унитарного пространства матрица сопряженного оператора получается из матрицы оператора переходом к транспонированной и комплексно сопряженной матрице:

. (7.6.3)

В ортонормированном базисе унитарного пространства сопряженному оператору соответствует сопряженная матрица, и обратно. В случае евклидова пространства таким же образом устанавливается соответствие между сопряженными операторами и транспонированными матрицами.

Линейный оператор , действующий в унитарном пространстве , называется самосопряженным или эрмитовым, если он совпадает со своим сопряженным оператором, т.е. если , или, что то же самое, для любых векторов и из

. (7.6.4)

Матрицей самосопряженного оператора в ортонормированном базисе является эрмитова матрица , для которой . Все собственные значения самосопряженного оператора являются действительными числами. Собственные векторы самосопряженного оператора, отвечающие различным собственным значениям, ортогональны.

Основным свойством самосопряженного оператора является то, что в унитарном пространстве существует ортонормированный базис, состоящий из собственных векторов этого оператора. Это означает, что самосопряженный оператор является оператором простой структуры, а среди матриц , приводящих эрмитову матрицу к действительной диагональной матрице , имеется унитарная матрица, для которой . Таким образом, эрмитова матрица обладает каноническим разложением с унитарной трансформирующей матрицей .

Эрмитов оператор называется неотрицательным (положительно определенным), если для любого ненулевого вектора выполняется неравенство . Неотрицательный и положительно определенный операторы обозначаются соответственно через и . Аналогично определяются и обозначаются неотрицательные и положительно определенные матрицы.

Линейный оператор , действующий в унитарно пространстве , называется унитарным, если . Другими словами, для унитарного оператора .

Унитарный оператор сохраняет скалярное произведение и длины векторов, т.е.

; (7.6.5)

(7.6.6)

Унитарный оператор любую ортонормированную систему векторов переводит в ортонормированную систему векторов, ортонормированный базис - в ортонормированный базис. Собственные значения унитарного оператора по модулю равны единице. В ортонормированном базисе пространства матрицей унитарного оператора является унитарная матрица, и обратно, если в ортонормированном базисе оператор имеет унитарную матрицу, то этот оператор унитарный. Столбцы (строки) унитарной матрицы, рассматриваемые как векторы унитарного арифметического пространства, образуют ортонормированную систему.

Основным свойством унитарного оператора является то, что в унитарном пространстве, в котором он действует, существует ортонормированный базис, состоящий из собственных векторов этого оператора. Это означает, что унитарный оператор является оператором простой структуры, а среди матриц , приводящих унитарную матрицу к диагональной матрице с диагональными элементами, равными по модулю единице, имеется унитарная матрица. Таким образом, унитарная матрица обладает каноническим разложением с унитарной трансформирующей матрицей и диагональной матрицей с диагональными элементами, равными по модулю единице.

Линейный оператор , действующий в унитарном (евклидовом) пространстве , называется нормальным, если он перестановочен со своим сопряженным оператором, т.е. если .

В ортонормированном базисе матрицей нормального оператора является матрица , перестановочная со своей сопряжённой матрицей, т.е. удовлетворяющая условию . Такие матрицы называются нормальными.

Основным свойством нормального оператора, действующего в унитарном пространстве, является то, что в этом пространстве существует ортонормированный базис, состоящий из собственных векторов этого оператора. Верно и обратное утверждение, т.е. если в унитарном пространстве существует базис, состоящий из собственных векторов оператора, то этот оператор нормальный.

Если оператор - нормальный, то собственные значения операторов и , соответствующие общему собственному вектору, комплексно сопряжены.

Примерами нормальных операторов являются эрмитовы и унитарные операторы.

Нормальный оператор является оператором простой структуры. На матричном языке это означает, что нормальная матрица приводится к диагональному виду. Нормальная матрица обладает каноническим разложением с унитарной трансформирующей матрицей.

У всякого линейного оператора в действительном линейном пространстве существует одномерное или двумерное инвариантное подпространство.

Линейный оператор , действующий в евклидовом пространстве , называется симметричным или самосопряженным, если для любых векторов и из выполняется равенство (7.6.4).

Матрицей симметричного оператора в ортонормированном базисе является симметричная матрица , для которой . Все собственные значения симметричного оператора являются действительными числами. Собственные векторы симметричного оператора, отвечающие различным собственным значениям, ортогональны.

Основным свойством симметричного оператора является то, что в евклидовом пространстве существует ортонормированный базис, состоящий из собственных векторов этого оператора. Это означает, что симметричный оператор является оператором простой структуры, а среди матриц , приводящих симметричную матрицу к диагональной матрице , имеется ортогональная матрица, для которой . Таким образом, симметричная матрица обладает каноническим разложением с ортогональной трансформирующей матрицей . Правило построения этой ортогональной матрицы отличается от рассмотренного в § 7.5 лишь тем, что здесь необходимо ортонормировать найденный базис из собственных векторов матрицы .

Симметричный оператор называется неотрицательным ( положительно определенным), если для любого ненулевого вектора выполняется неравенство . Так же определяются одноименные классы действительных матриц.

Линейный оператор , действующий в евклидовом пространстве , называется ортогональным, если он сохраняет скалярное произведение любых векторов и из , т.е. если выполняется равенство

. (7.6.7)

Ортогональный оператор сохраняет длины векторов и углы между векторами. Ортогональный оператор любую ортонормированную систему векторов переводит в ортонормированную систему векторов, а ортонормированный базис - в ортонормированный базис. Ортогональный оператор в любом ортонормированном базисе евклидова пространства имеет ортогональную матрицу. Определитель матрицы ортогонального оператора равен .

Для любого ортогонального оператора , действующего в - мерном евклидовом пространстве , существует в ортонормированный базис , в котором матрица оператора имеет следующий вид

, (7.6.8)

где все невыписанные элементы равны нулю.

Пример 1. Линейный оператор в базисе , , имеет матрицу . Найдите матрицу сопряженного оператора в этом же базисе, если векторы заданы координатами в ортонормированном базисе .

Решение. Матрица сопряженного оператора в базисе связана с матрицей этого же оператора в базисе соотношением , где - матрица перехода от базиса к базису . Поскольку для евклидова пространства в ортонормированном базисе матрицей сопряженного оператора является транспонированная матрица к матрице оператора , . Матрицу оператора в базисе найдем через матрицу этого же оператора в базисе по формуле , где - матрица перехода от базиса к базису . Очевидно, что . В силу того, что , а , получаем:

Пример 2. В базисе скалярное произведение задано формулой

, (7.6.9)

а линейный оператор - матрицей . Найдите матрицу сопряженного оператора в том же базисе .

Решение. Начнем с построения ортонормированного базиса . Зная , можно по формуле вычислить матрицу оператора в этом базисе (здесь - матрица перехода от базиса к базису ) и найти матрицу сопряженного оператора в базисе . Матрицу сопряженного оператора в базисе найдем при помощи соотношения , где - матрица перехода от базиса к базису . В силу того, что .

Построение ортонормированного базиса осуществим, применяя процесс ортогонализации Грама - Шмидта и нормирование векторов

Векторы ортогональны в смысле скалярного произведения (7.6.9). Учитывая, что , получаем:

Таким образом, матрица перехода от базиса к ортонормированному базису

,

а обратная к ней матрица

.

Отсюда следует, что

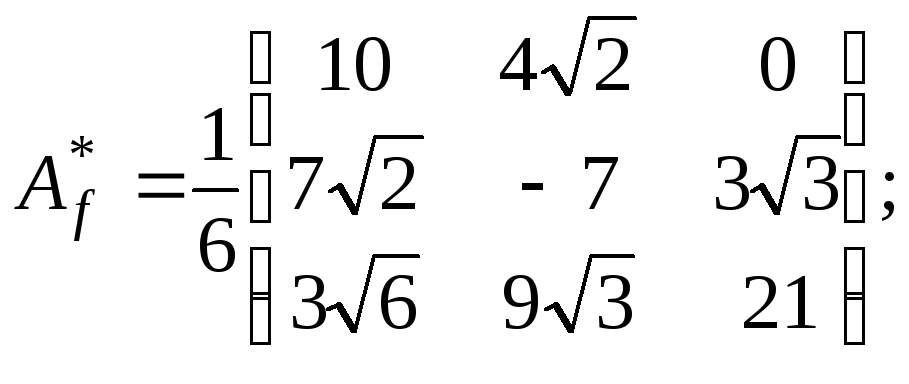
Пример 3. Для симметричной матрицы постройте каноническое разложение с ортогональной трансформирующей матрицей и, пользуясь им, найдите .

Решение. Характеристический многочлен

имеет корни . Поэтому матрицей в каноническом разложении является .

Перейдем к построению ортогональной матрицы в каноническом разложении. Найдем собственные векторы , отвечающие собственным значениям .

.

Общим решением однородной системы является вектор . Выбирая , получаем .

.

Общим решением однородной системы является вектор . Выбирая , получаем . Подчеркнем, что и сразу ортогональны как собственные векторы симметричного оператора, отвечающие различным собственным значениям. Поскольку , получаем ортонормированную систему собственных векторов матрицы , являющуюся столбцами искомой транформирующей матрицы, т.е. .

Проверим правильность построения канонического разложения . Учитывая, что , имеем:

Полученное каноническое разложение позволяет вычислить по формуле , где .

Пример 4. Линейный оператор пространства в базисе , , задан матрицей . Является ли ортогональным оператором?

Решение. Найдем матрицу оператора в ортонормированном базисе , , и проверим, будет ли полученная матрица ортогональной.

,

где - матрица перехода от базиса к базису . Поскольку , , , матрица перехода от базиса к базису

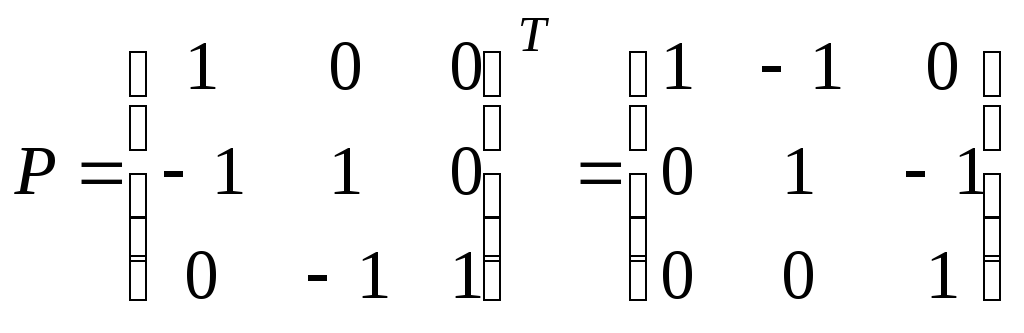. Следовательно, , и

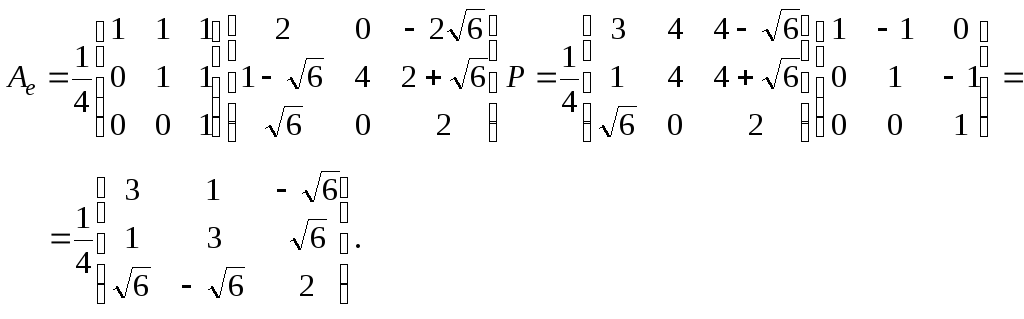
В силу того, что

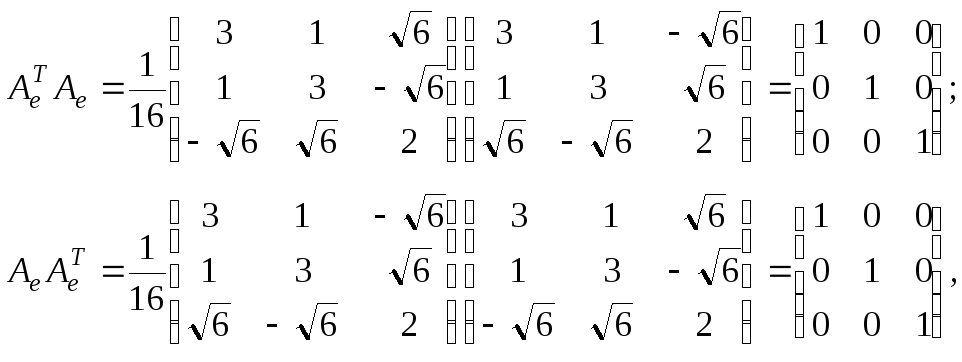
отсюда заключаем, что является ортогональным оператором.

Пример 5. Ортогональный оператор в ортонормированном базисе имеет ортогональную матрицу . Постройте базис , в котором оператор имеет матрицу канонического вида (7.6.8) и найдите матрицу .

Решение. Характеристический многочлен

оператора имеет корни .

В силу того, что

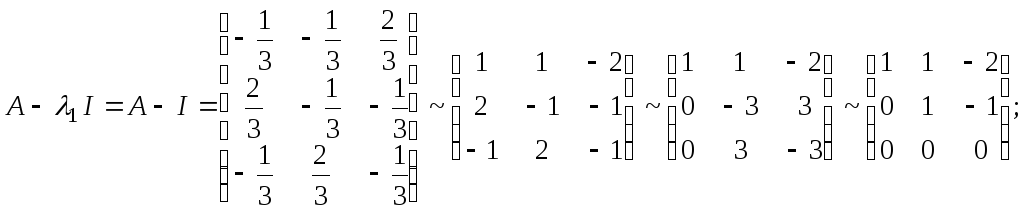
однородная система имеет общее решение , а однородная система имеет общее решение . Выбирая и , получаем векторы и . Заметим, что векторы ортогональны (см. задачи 7.6.40 и 7.6.46). Нормируя их, придем к искомому базису

в котором оператор имеет каноническую матрицу

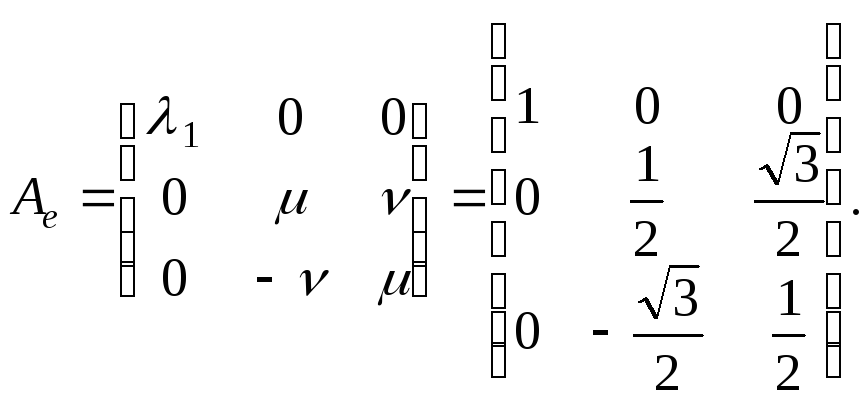
Проверим правильность вычислений:

где

7.6.1. Из определения сопряженного оператора выведите следующие свойства:

а)

б)

в)

г)

д)

е)

ж) если оператор невырожден, то

з) для всякого целого неотрицательного ;

и) если оператор невырожден, то свойство з) имеет место для любого целого числа ;

к) если - произвольный многочлен, то , где .

7.6.2. Докажите, что свойства, перечисленные в предыдущей задаче, выполняются и для сопряженных матриц.

7.6.3. Покажите, что если операторы и перестановочны, то перестановочны и сопряженные и операторы и (операторы и из называются перестановочными, если ).

7.6.4. Пусть - ортогональный (но не ортонормированный!) базис пространства . Найдите связь между матрицами в этом базисе оператора из и сопряженного оператора .

7.6.5. Пусть оператор действует в одномерном унитарном (евклидовом) пространстве. В чем состоит преобразование , сопряженное по отношению к ?

7.6.6. Пусть - ортонормированный базис евклидова пространства, - матрица линейного оператора в базисе . Найдите матрицу оператора в базисе .

7.6.7. Линейный оператор евклидова пространства в базисе , , задан матрицей 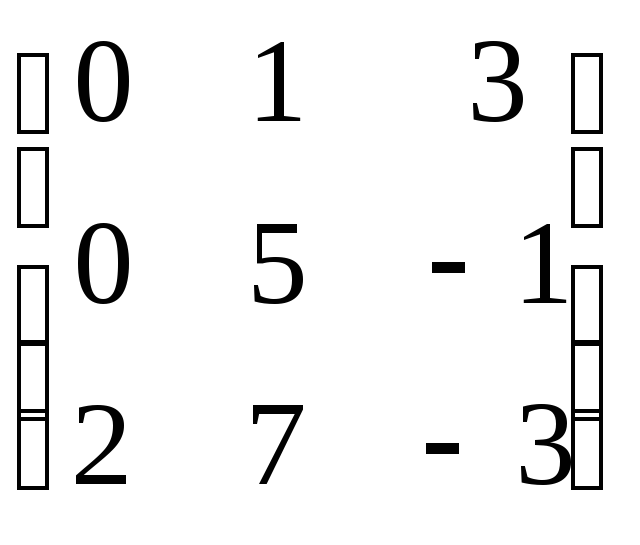. Найдите матрицу оператора в том же базисе, считая, что координаты векторов базиса даны в некотором ортонормированном базисе.

7.6.8. Найдите матрицу линейного оператора в ортонормированном базисе , если переводит векторы , , в векторы , , соответственно, считая, что координаты всех векторов даны в базисе .

Пусть в некотором базисе скалярное произведение задано билинейной формой , а линейный оператор - матрицей . Найдите матрицу сопряженного оператора в том же базисе:

7.6.9.

.
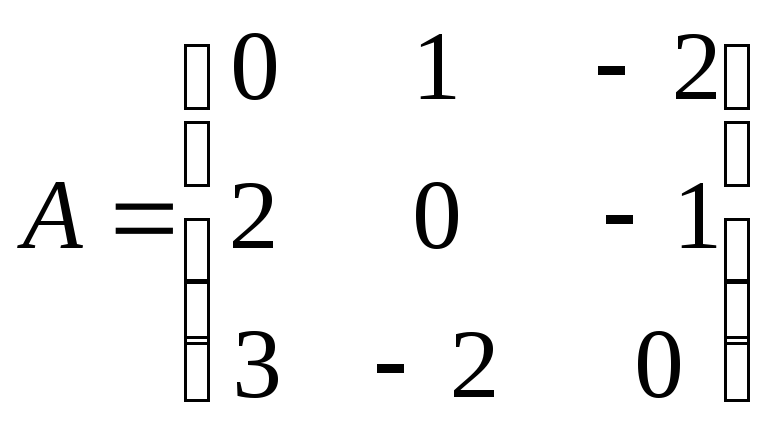