Глава 3 Линейные пространства

§ 3.1. Определение линейного пространства

Линейным (векторным) пространством над полем называется множество элементов (векторов) удовлетворяющих следующим аксиомам:

А. Каждой паре элементов и из поставлен в соответствие элемент этого множества, называемый суммой элементов и и обозначаемый , причем

Сложение коммутативно, т.е.

Сложение ассоциативно, т.е.

В множестве существует нулевой элемент такой, что

В множестве для любого элемента существует противоположный элемент такой, что

В. Каждому элементу и каждому числу отвечает элемент этого множества , называемый произведением элемента на число , причем

С. Операции сложения векторов и умножения вектора на число связаны между собой соотношениями

т.е. умножение на число дистрибутивно относительно сложения векторов;

т.е. умножение дистрибутивно относительно сложения чисел.

Если есть поле действительных или комплексных чисел, то линейное пространство над называется соответственно действительным или комплексным.

Пример 1. Множество состоит из одного элемента . Операции в определены следующим образом:

Проверьте, что является линейным пространством над полем .

Решение. Поскольку и , перейдем непосредственно к проверке аксиом линейного пространства:

является нулевым элементом в , т.к.

выполняет роль противоположного элемента в , т.к.

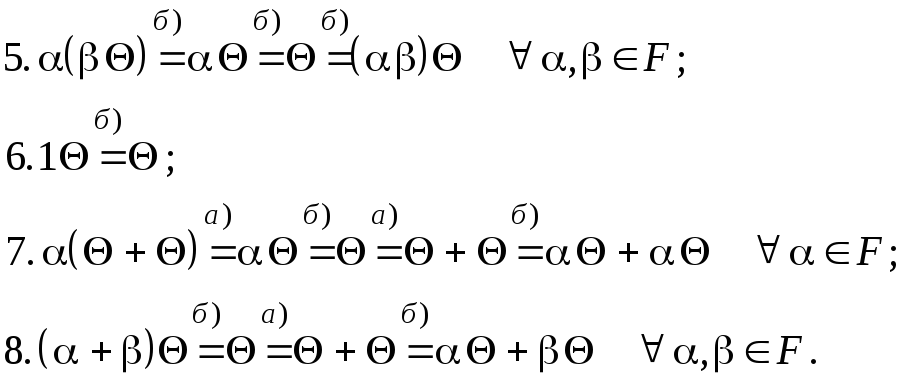
Поскольку все аксиомы линейного пространства выполнены, заключаем, что является линейным пространством над полем (оно называется тривиальным).

Пример 2. В множестве положительных действительных чисел определены следующие операции:

“сложение” (т.е. обычное умножение чисел и );

“умножение на действительное число” (т.е. возведение числа в степень ).

Проверьте, что множество с указанными операциями является линейным пространством.

Решение. Очевидно, что и . Проверим аксиомы линейного пространства.

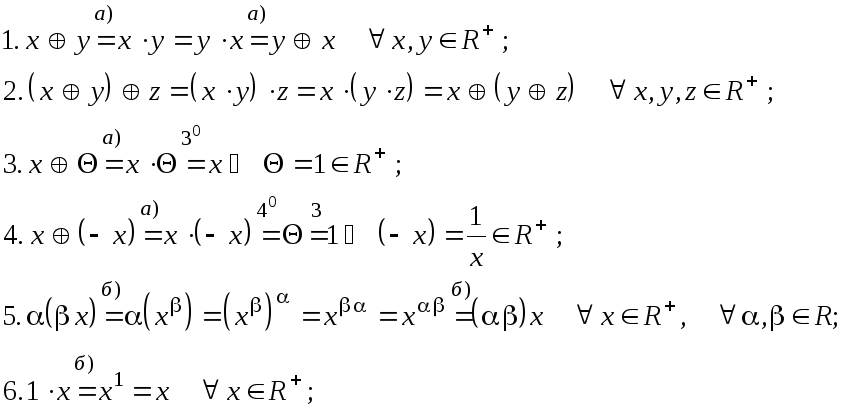
Все аксиомы линейного пространства выполнены. Следовательно, является действительным линейным пространством.

Пример 3. Пусть - множество всех упорядоченных пар действительных чисел с операциями:

если и , то

для любого действительного числа

Будет ли действительным линейным пространством ?

Решение. Ясно, что и . Проверим аксиомы линейного пространства.

т.е.

т.е.

Поскольку восьмая аксиома не выполнена, не является действительным линейным пространством.

Для каждого из следующих множеств векторов на плоскости определите, является ли это множество линейным пространством относительно обычных операций сложения векторов и умножения вектора на число. В случае отрицательного ответа укажите какие именно аксиомы линейного пространства не выполнены. Предполагается, что начало каждого вектора находится в фиксированной точке плоскости, являющейся началом прямоугольной системы координат.

3.1.1. Все векторы, концы которых лежат на данной прямой.

3.1.2. Все векторы, концы которых лежат: в первой четверти системы координат; в первой или третьей четверти; в первой или во второй четверти.

3.1.3. Являются ли действительными линейными пространствами следующие множества чисел с обычными операциями сложения и умножения:

- множество всех натуральных чисел;

- множество всех целых чисел;

- множество всех действительных чисел;

- множество всех комплексных чисел;

- множество всех положительных действительных чисел?

3.1.4. Пусть - множество всех упорядоченных наборов по элементов поля : . Операции в заданы правилами:

если и , то

;

для любого из поля

.

Проверьте, что является линейным пространством над полем . Если или , то называют действительным или комплексным арифметическим пространством и обозначают соответственно или .

3.1.5. Пусть - поле из двух элементов и , в котором операции заданы следующими табличками:

сложение умножение

0 1 0 1

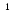
Постройте линейное пространство (см. задачу 3.1.4.). Покажите, что для любого вектора из Найдите число векторов в .

3.1.6. Являются ли линейными пространствами над полем следующие множества матриц с обычными операциями сложение матриц и умножения матриц на элемент поля :

- множество всех прямоугольных -матриц с действительными

элементами ;

3.1.7. Выясните, являются ли действительными линейными пространствами следующие множества многочленов от одной переменной с действительными коэффициентами:

множество всех многочленов степени

множество всех многочленов степени

множество всех многочленов удовлетворяющих условию множество всех многочленов удовлетворяющих условию

3.1.8. Является ли действительным линейным пространством множество бесконечных последовательностей действительных чисел (Фибоначчи), элементы которых удовлетворяют соотношению

Операции над последовательностями определены следующим образом:

если то

для любого действительного