3Линейка / Задачник-1 / Глава 3(2)

§ 3.4. Базис и размерность линейного пространства

Всякую систему векторов линейного пространства называют базисом этого пространства, если эта система векторов линейно независима и любой вектор пространства линейно выражается через векторы этой системы.

Существенно различными являются случаи, когда базис пространства конечен и когда он бесконечен. В линейной алгебре изучаются линейные пространства с конечными базисами. Линейное пространство называют конечномерным, если оно обладает базисом, состоящим из конечного числа векторов. Конечномерное пространство может обладать многими различными базисами. Число векторов в каждом базисе конечномерного пространства одинаково. Это число называют размерностью пространства. Если размерность пространства равна , то записывают . Пространство при этом называют - мерным.

Пусть в линейном пространстве над полем задан некоторый базис

.

Произвольный вектор пространства линейно выражается через базис :

Представление вектора в виде называется разложением по базисным векторам , а коэффициенты в разложении - координатами вектора в базисе .

Два линейных пространства и над полем называют изоморфным, если между их векторами можно установить взаимно однозначное соответствие, при котором образом суммы двух векторов служит сумма образов этих векторов, а образом произведения вектора на число служит произведение образа этого вектора на то же число, т.е. если из того, что

следует и

Необходимым и достаточным условием изоморфного соответствия двух линейных пространств является совпадение их размерностей.

При изоморфизме линейно независимым векторам из соответствует линейно независимые векторы из и наоборот.

Пример 1. Выясните, какова размерность каждого из указанных линейных пространств, и найдите какой- либо базис пространства:

арифметическое пространство , векторами которого являются упорядоченные наборы по действительных чисел (см. задачу );

пространство многочленов с действительными коэффициентами от одной переменной, степень которых не превышает заданного неотрицательного числа (см. задачу ));

пространство прямоугольных - матриц с действительными элементами (см. задачу )).

Решение. Одним из возможных базисов является следующий:

Действительно, система векторов линейно независима

и всякий вектор линейно выражается через векторы этой системы (если , то ). Следовательно,

Простейшим базисом является такая система векторов:

Очевидно, что система векторов линейно независима

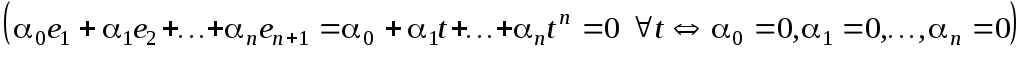
и любой вектор линейно выражается через векторы этой системы

(если то ). Таким образом, и изоморфно .

За базис пространства можно принять систему векторов

(3.4.5)

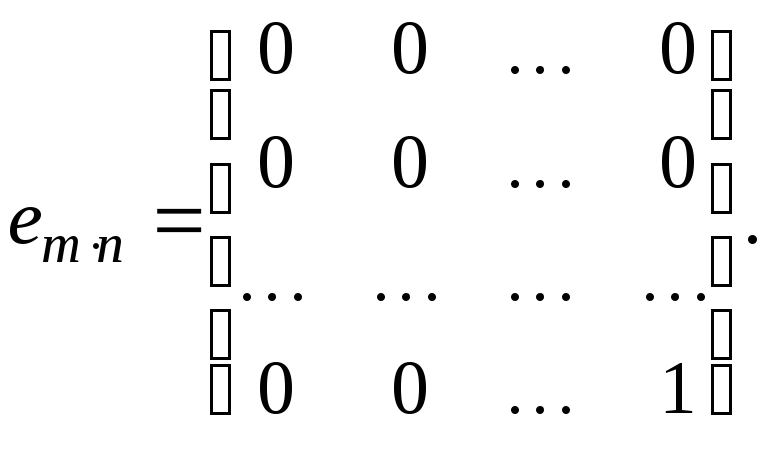
Она линейно независима (

) и через неё линейно выражается любой вектор ( если то

). Поэтому и изоморфно

Пример 2. Систему многочленов дополните до базиса пространства

Решение. Известно (см. предыдущий пример), что Выясним, сколько и каких векторов нужно взять, чтобы дополнить данную систему векторов до базиса Воспользуемся изоморфизмом между и в котором и будем работать (это проще).

.

Сведём векторы в матрицу и приведём её элементарными преобразованиями к ступенчатому виду:

Очевидно, что система векторов (а, значит и система векторов ) линейно независима. Дополнять до базиса нужно двумя векторами. Например, и

Пример3. Проверьте, что векторы образуют базис пространства и найдите координаты вектора в этом базисе.

Решение. Нужно показать, что векторы линейно независимы.

Значит, можно вектор разложить по базисным векторам, т.е. представить в виде , причём такое представление будет единственным.

Отсюда

или в матричном виде

Заметим, что столбцами этой матрицы являются векторы Решим систему метом Гаусса:

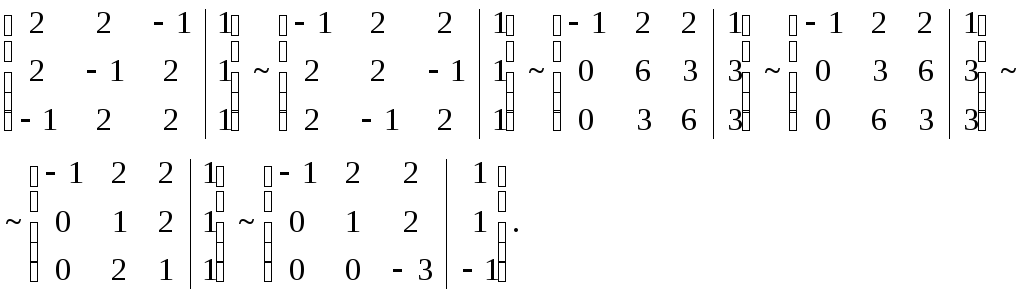
Следовательно,

Таким образом, вектор в базисе имеет координаты

3.4.1. Выясните, какова размерность каждого из указанных линейных пространств, и найдите какой-либо базис пространства:

пространство (см. пример 2 § 3.1. ) ;

пространство (см. задачу 3.1.3 ) ;

пространство комплексных чисел , рассматриваемое как действительное линейное пространство (см. задачу 3.1.3. ) ;

пространство комплексных чисел , рассматриваемое как комплексное линейное пространство ;

пространство, заданное в задаче 3.1.6.;

пространство, заданное в задаче 3.1.6 ;

пространство бесконечных действительных последовательностей, элементы которых удовлетворяют соотношению

(см. задачу 3.1.8.).

3.4.2. В пространстве найдите два различных базиса, имеющих общие векторы и

3.4.3. В базисе действительного линейного пространства найдите координаты вектора

3.4.4. В базисе действительного линейного пространства найдите координаты векторов

и

3.4.5. В пространстве дана система векторов .

Можно ли принять эту систему за базис? Каковы координаты вектора в этом базисе?

3.4.6. Можно ли в пространстве многочленов выбрать в качестве базиса систему многочленов

3.4.7. Найдите координаты многочлена в каждом из следующих базисов пространства

§ 3.5. Подпространства линейного пространства.

Сумма и пересечение подпространств

Множество векторов линейного пространства называется подпространством этого пространства, если : сумма любых двух векторов из принадлежит и произведение каждого вектора из на любое число из поля также принадлежит .

Рассмотрим два подпространства и линейного пространства .

Суммой подпространств и называется множество всех векторов, которые можно представить в виде , где и принадлежат соответственно подпространствам и . Сумма подпространств и обозначается .

Пересечением подпространств и называется множество векторов, которые принадлежат одновременно обоим подпространствам. Пересечение подпространств и обозначается .

Сумма и пересечение подпространств и являются подпространствами пространства .

Для любых двух подпространств , конечномерного пространства имеет место равенство

Если для каждого вектора из представление

единственно, то называется прямой суммой подпространств и и обозначается .

Сумма подпространств тогда и только тогда будет прямой суммой, когда объединение базисов этих подпространств дает базис .

Пример 1. Покажите, что множество всех векторов из , координаты которых удовлетворяют уравнению является подпространством линейного пространства . Найдите один из базисов и размерность этого подпространства.

Решение. Обозначим

.

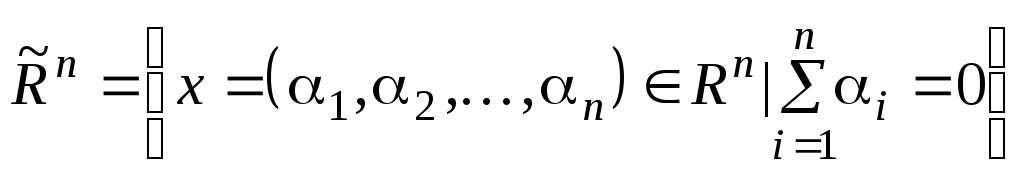Множество замкнуто относительно сложения векторов и умножения вектора на действительное число:

, т.е.

, т.е.

Следовательно, - подпространство линейного пространства .

Покажем, что система векторов

образует базис в :

если и только если , т.е. система векторов линейно независима;

=, т.е. всякий вектор может быть представлен в виде линейной комбинации системы векторов .

Таким образом,

Пример 2. Найдите базисы суммы и пересечения подпространств

и , где

Решение. Сначала найдем базисы подпространств и

.

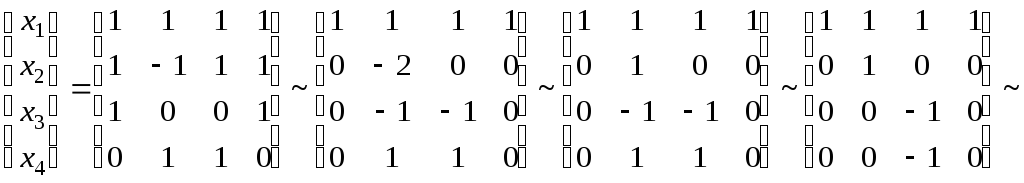
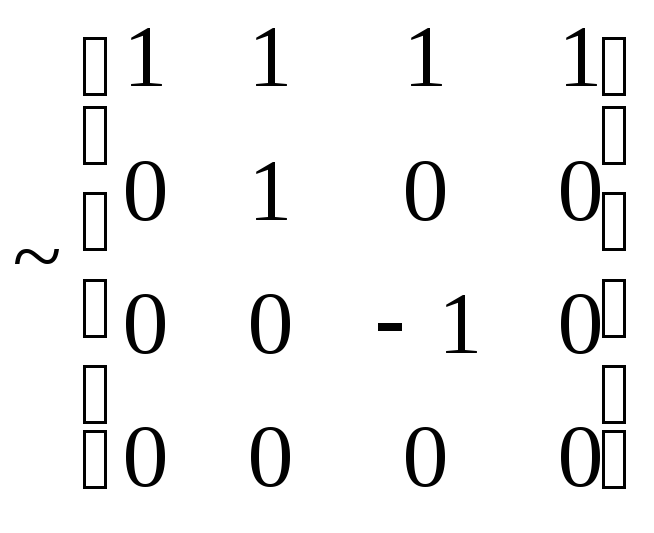Базис образуют векторы ,

Базис образуют векторы ,

.

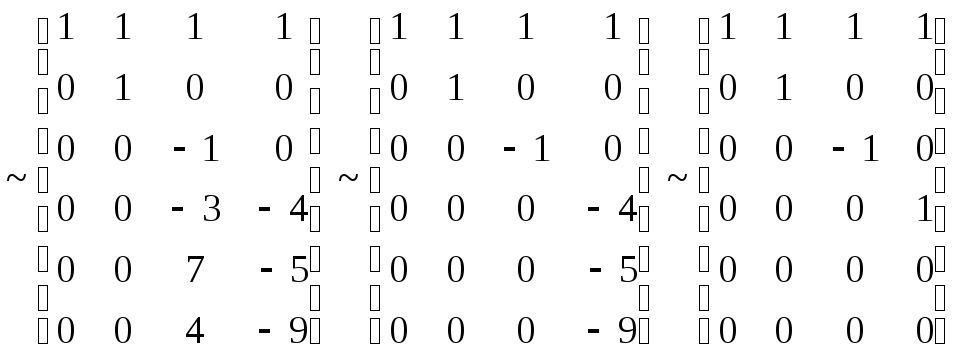Базис составляют вектора ,

Размерность пересечения подпространств и определим из соотношения

.

Обозначим базисные вектора подпространства через и . По определению пересечения подпространств

или

где слева от равенства записана линейная комбинация векторов, образующих базис . Переменные и , стоящие при линейно зависимых векторах, называются свободными. Выберем их значения в соответствии с таблицей

i
1	1	0
2	0	1

При таком выборе значений и системы линейных уравнений относительно ,,, будут иметь линейно независимые решения. Запишем явно системы и решим их методом Гаусса. Учитывая, что системы уравнений отличаются лишь правыми частями, целесообразно их объединить в одну расширенную матрицу.