
- •Классические ортогональные полиномы
- •Интегралы с полиномами Эрмита
- •Гармонический осциллятор
- •Примеры
- •3. Доказать, что фурье-преобразование не изменяет форму уравнения гармонического осциллятора.
- •Обобщенные полиномы Лагерра
- •Уравнение Лагерра
- •Формула Родрига
- •Полиномиальное представление
- •Полиномы низших степеней
- •Производящая функция
- •Рекуррентные соотношения
- •2. Дифференцируя далее (6.54), получаем
- •Следует
- •Связанные состояния электрона в АтомЕ водорода Характеристики атома протия
- •Решение уравнения методом факторизации
- •Физический смысл параметров
- •Частные случаи
- •Полиномы Лежандра
- •Уравнение Лежандра
- •Метод факторизации
- •Представление в виде полинома
- •Полиномы низших порядков
- •Дифференцируем
- •. (6.132)
- •7. Складываем (6.128) и (6.130)
- •Интегралы с полиномами лежандра
- •Полиномы Чебышева первого рода
- •Уравнение Чебышева
- •Метод факторизации
- •Тригонометрическое представление
- •Полиномы Чебышева второго рода
- •Разложения функции
- •Аппроксимация полиномом
Примеры
1. Для матричного элемента оператора координаты гармонического осциллятора доказать
 ,
(П.4.6)
,
(П.4.6)
где
 – безразмерная,
– безразмерная,
 .
.
Для
оператора
![]() по определению
по определению
 .
.
Устраняем множитель x под интегралом рекуррентным соотношением
 ,
(6.34)
,
(6.34)
тогда

 .
.
Вычисляем интегралы при помощи условия ортонормированности
 .
(6.33)
.
(6.33)
Получаем
 ,
(П.4.6)
,
(П.4.6)
В частности
 ,
,
 ,
,
![]() .
(П.4.7)
.
(П.4.7)
Матричные элементы вещественные, тогда из
![]() (4)
(4)
получаем
![]() .
.
2.
Для оператора импульса
![]() найти матричный
элемент
найти матричный
элемент
 ,
,
где
 ;
;
 ;
;
 – безразмерная.
– безразмерная.
В
![]() устраняем производную под интегралом,
используя рекуррентное соотношение:
устраняем производную под интегралом,
используя рекуррентное соотношение:
 .
(6.39)
.
(6.39)
Получаем

Вычисляем интегралы при помощи условия ортонормированности
 ,
,
находим
 .
.
Частные результаты:
 ,
,
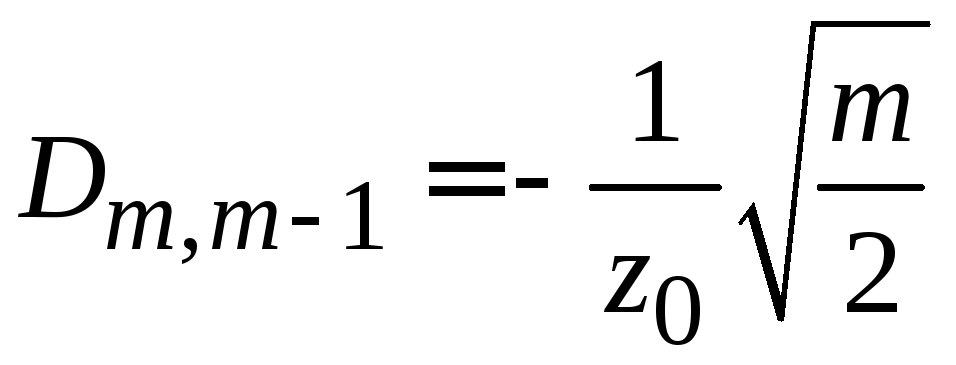 ,
,
![]() .
.
Матричные элементы импульса:
 ,
(П.4.11)
,
(П.4.11)
 ,
,
 ,
,
 ,
,
 ,
,
![]() ,
,
среднее значение
![]() .
(П.4.12)
.
(П.4.12)
3. Доказать, что фурье-преобразование не изменяет форму уравнения гармонического осциллятора.
Фурье-преобразование уравнения
 (6.31)
(6.31)
с учетом
 ,
(1.35)
,
(1.35)
 (1.37)
(1.37)
дает
![]()
 .
.
Заменяем
![]() ,
получаем
,
получаем
 ,
(П.4.14)
,
(П.4.14)
где
![]() – безразмерный импульс;
– безразмерный импульс;
 .
(П.4.15)
.
(П.4.15)
4. Для полиномов Эрмита доказать формулу Мелера
 ,
(П.4.20)
,
(П.4.20)
где
![]() .
Получить формулу при
.
Получить формулу при![]() .
.
Используем интегральное представление полиномов Эрмита
 ,
,
 .
(6.8)
.
(6.8)
Меняем порядок суммирования и интегрирований
 .
.
Учитываем
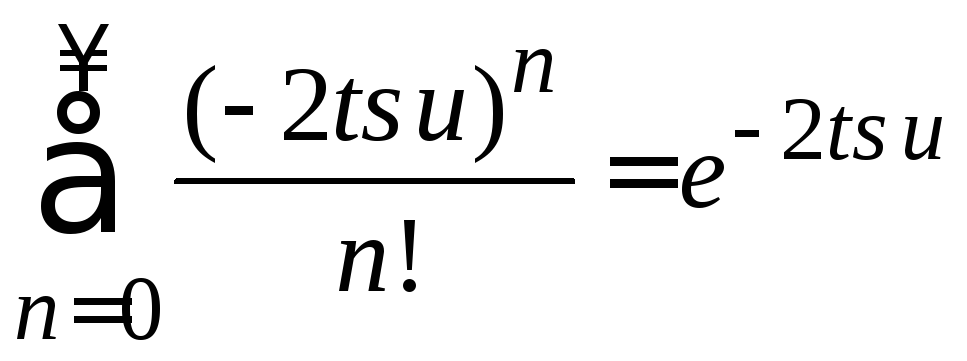 ,
,
тогда
 .
.
Используем
 (П.2.5)
(П.2.5)
при
![]() ,
,
![]() ,
, ,
,
и вычисляем внутренний интеграл
 ,
,
тогда
 .
(П.4.20а)
.
(П.4.20а)
Последний интеграл находим при помощи (П.2.5)
 ,
,
![]() ,
,
и получаем (П.4.20).
При
![]() последний интеграл дает дельта-функцию
последний интеграл дает дельта-функцию
 ,
,
где учено
 .
(2.24)
.
(2.24)
Из
(П.4.20а)
получаем условие
полноты базиса
![]()
 .
(П.4.21)
.
(П.4.21)
Для
базиса функций гармонического осциллятора
![]() ,
где
,
где
 ,
(6.32)
,
(6.32)
получаем условие полноты
 .
(П.4.22)
.
(П.4.22)
Обобщенные полиномы Лагерра
![]() ,
,
![]() ;
;![]() – любое число;
– любое число;![]() .
.
Набор
полиномов образует ортонормированный
базис на полуоси
![]() .
.
Используются:
в теории измерительной техники и в теории систем связи;
в квантовой механике описывают радиальное движение электрона в атоме.
Полиномы
![]() исследовал Эдмон Никола Лагерр в 1878 г.
исследовал Эдмон Никола Лагерр в 1878 г.
Обобщенные
полиномы
![]() изучал Николай Яковлевич Сонин в 1880 г.,
поэтому их называют такжеполиномами
Сонина–Лагерра.
изучал Николай Яковлевич Сонин в 1880 г.,
поэтому их называют такжеполиномами
Сонина–Лагерра.
Уравнение Лагерра
![]() (6.41)
(6.41)
является гипергеометрическим уравнением.
Формула Родрига
Методом факторизации ранее получена весовая функция
![]() .
(П.3.9)
.
(П.3.9)
Из (П.3.10) при
![]()
находим
 .
(6.42)
.
(6.42)
Полиномиальное представление
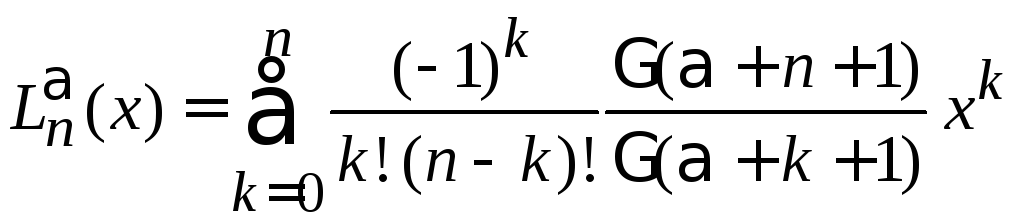 ,
(6.44)
,
(6.44)
где
n
– высшая степень полинома
![]() .
.
Доказательство (6.44):
Дифференцирование в (6.42) проводим по формуле Лейбница
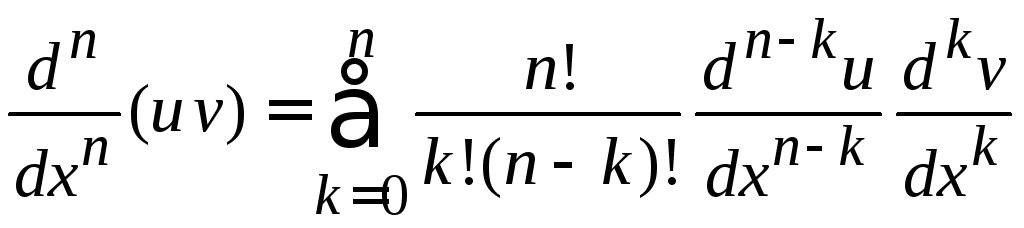 .
(6.45)
.
(6.45)
Например,
при
![]() получаем известную формулу
получаем известную формулу
 .
.
В
(6.45) полагаем
![]() ,
,![]() и учитываем
и учитываем
 .
.
Соотношение

обобщаем
на случай
![]() – не целое
– не целое
 .
.
В результате
 .
.
Подставляем в
 ,
(6.42)
,
(6.42)
получаем полином порядка n
 .
(6.44)
.
(6.44)
Из (6.44)
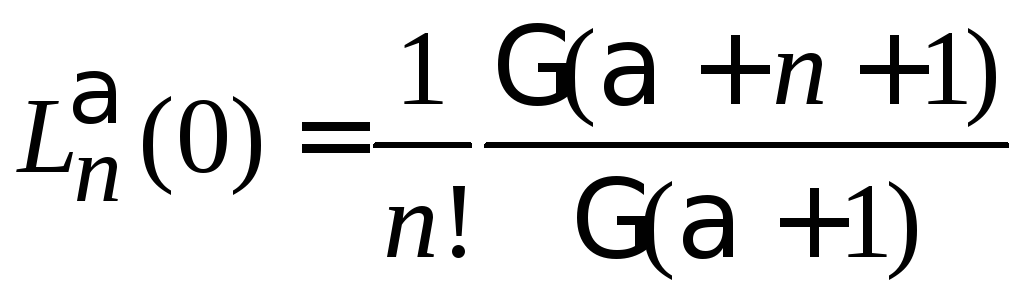 .
(6.47)
.
(6.47)
