ГАММА- И БЕТА-ФУНКЦИИ ЭЙЛЕРА

Гамма-функция

. (4.1)

Является обобщением факториала на случай произвольного аргумента. Функцию исследовал Леонард Эйлер в 1730 г.

Анализ интеграла

Область интегрирования разбиваем на участки и

,

где

, .

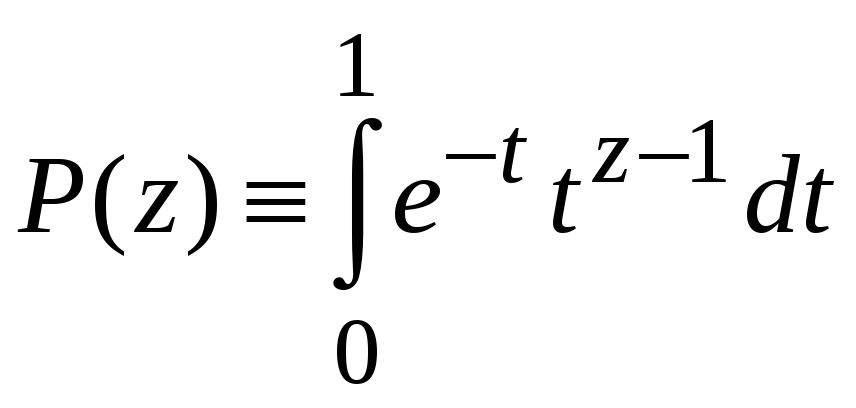1. Функция конечна при любых z.

Доказательство:

На верхнем пределе убывает с ростом t быстрее любой степенной функции, и интеграл сходится при любых z.

На нижнем пределе

– конечно при любых z.

2. Функция имеет полюса первого порядка при

Доказательство:

В интеграл подставляем

,

получаем

При положительном используем , тогда

– конечное,

где учтено

.

При отрицательном , где , для получаем

.

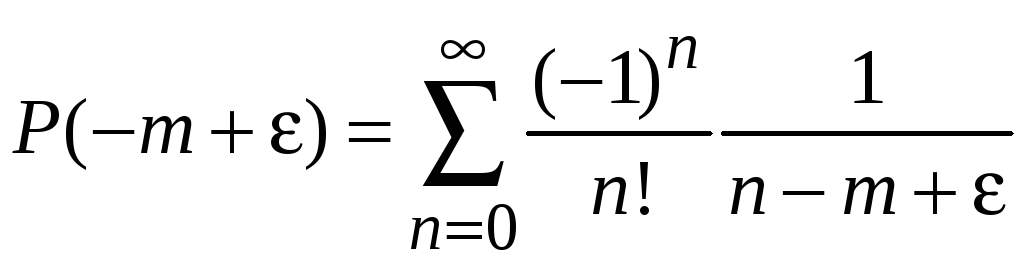Слагаемое дает полюс первого порядка, тогда

, (4.3)

. (4.4)

Доказательство (4.4):

Из (4.3)

.

Рекуррентное соотношение

В рекуррентном соотношении одна функция встречается более одного раза, от лат. recurro – «возвращаться». Интегрируем по частям

,

где

, ,

, ,

. (4.5)

Связь с факториалом

,

Из (4.5):

при , ;

при , ;

при , ;

,

, (4.6)

. (4.7)

Интегралы, выражающиеся через гамма-функцию

В (4.1)

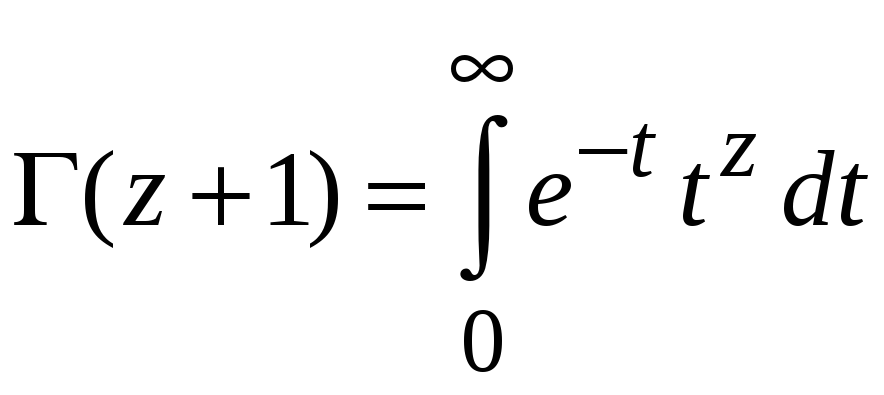
замена аргумента

,

дает

,

переобозначаем :

. (4.8)

В (4.8) полагаем

, , ,

получаем

,

,

. (4.8а)

В интеграле

(4.8)

заменяем аргумент

, , ,

получаем

,

где заменен параметр

, .

В полученном выражении

переобозначаем и

. (4.9)

Интеграл Пуассона

Из (4.9) при

,

получаем

. (4.9а)

Произведение гамма-функций

В (4.1)

,

замены

, ,

,

дают

.

Переходим к полярным координатам :

, , ,

,

получаем

.

Первый интеграл после замены равен , тогда

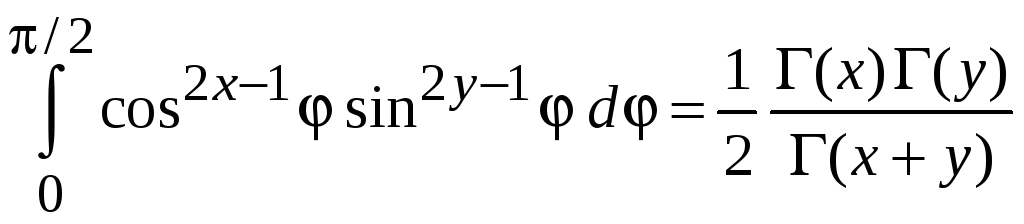. (4.10)

Гамма-функция полуцелого аргумента

Из (4.10) при с учетом :

Из при :

,

,

.

Из при :

,

,

, (4.11)

где учтено

.

Бета-функция

(4.13)

Связь с гамма-функцией

В (4.13) заменяем аргумент

, , ,

, ; , ,

получаем

,

сравниваем с

. (4.10)

Следовательно,

, (4.14)

. (4.15)

Интеграл со степенными функциями

В (4.14) заменяем аргумент

, ,

,

, ,

,

и параметры

, ,

находим

. (П.2.3)

Формула удвоения

Из

(4.13)

при

.

Учтен график подынтегральной функции .

Заменяем аргумент

,

,

,

получаем

,

где учтены

. (4.13)

Используем

. (4.14)

находим

,

.

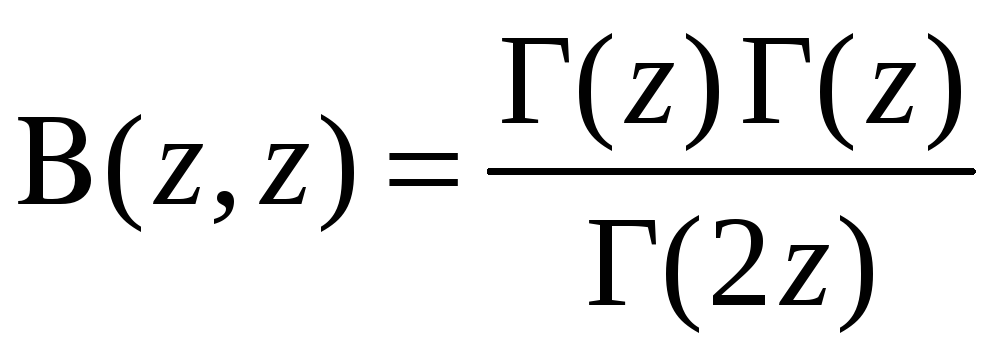Получаем формулу удвоения

. (4.16)

Формула дополнения

Из

(4.10)

при , получаем

, (4.18а)

где сделана замена

,

,

,

, ,

, .

Последнее равенство в (4.18а) – справочный интеграл. В результате

. (4.18)

В (4.18) замена с учетом дает

. (4.19)

В (4.18) замена с учетом дает

. (4.20)

В (4.20) используем

. (4.21)

В (4.20) используем

. (4.22)

Гамма-функция отрицательного полуцелого аргумента

Из

(4.18)

при

,

используем

,

получаем

.

Учитываем

, (4.11)

находим

. (4.17)

Частные результаты

,

,

.

Формула Стирлинга

Факториал с большим аргументом

, . (4.23)

Получил Джеймс Стирлинг в 1730 г. Для доказательства (4.23) используем

. (4.7)

Интеграл вычисляем по формуле Лапласа.

Асимптотическая формула Лапласа

В асимптотическом пределе выполняется приближенная формула

. (4.24)

Получил Пьер Симон Лаплас (1749–1827).

Доказательство:

Если , то сильно изменяется даже при малой вариации . Поэтому главный вклад в интеграл

вносит область t около – положения максимума . Условия максимума

, .

Разлагаем в ряд Тейлора около точки и оставляем первые три слагаемые

.

Если положение максимума находится далеко от концов области интегрирования , то они не вносят заметного вклада в интеграл, поэтому полагаем

, .

В результате

,

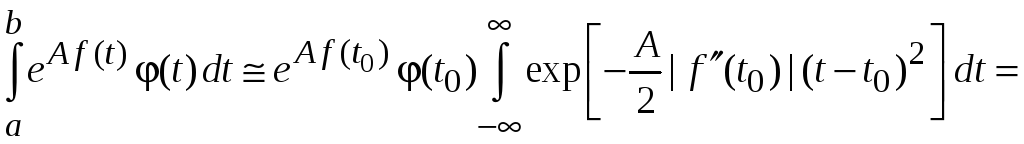
где заменен аргумент . Используем интеграл Пуассона

, (4.9а)

где и получаем

. (4.24)

Доказательство формулы Стирлинга

. (4.23)

Используем

,

где

,

,

.

Используем формулу Лапласа

(4.24)

при

, , , ,

получаем

. (4.24а)

Находим из условия :

,

, ,

,

,

,

,

и из (4.24а) получаем формулу Стирлинга

. (4.23)

Учет большего числа членов разложения в ряд Тейлора дает

. (4.26)

Пример 1

Доказать

, . (П.2.5)

Слагаемое в показателе экспоненты (П.2.5) устраняем заменой , тогда

.

Полагаем , находим

,

тогда

.

Интеграл дает

.

Используем интеграл Пуассона

, (4.9а)

получаем (П.2.5).

Пример 2

Фурье-образ функции Гаусса

Выполняется

,

в явной форме

. (П.2.6)

При получаем

.

Функция Гаусса инвариантна при преобразовании Фурье.

Доказательство (П.2.6):

Используем

, (П.2.5)

с параметрами

, , ,

и получаем (П.2.6).

Пример 3

Выполняется

, , (П.2.16)

где

, (П.2.17)

– дзета-функция, введена Леонардом Эйлером. Формулы (П.2.16) и (П.2.17) используются в квантовой статистике Ферми–Дирака и Бозе–Эйнштейна.

Частные значения:

, ,

, ,

, . (П.2.18)

Доказательство (П.2.16):

Упрощаем интеграл заменой :

.

Преобразуем интеграл к виду

.

Для этого используем разложение в ряд Маклорена

,

тогда

.