Рекуррентные соотношения
1. Подставляем (8.57)
в (8.37)
при
.
Получаем
.
(8.70)
2. Подставляем
,
в (8.36)
при
.
Получаем
.
Из (8.70) выражаем
,
подставляем в последнее равенство, и получаем
.
(8.71)
3. Выполняются соотношения
,
(8.72)
,
(8.73)
,
(8.74)
.
(8.75)
Функция Эйри первого рода
,
Описывает:
– дифракцию волн,
– состояние квантовой частицы в однородном поле,
– состояние частицы в треугольной потенциальной яме,
– состояние частицы вблизи точки поворота классического движения.
Функцию ввел английский астроном Эйри в 1838 г. при исследовании дифракции света.
Сэр Джордж Биддель Эйри (1801–1892)
Директор Гринвичской обсерватории, президент Лондонского королевского общества. Разработал теорию дифракции света на объективе телескопа. Центральное светлое пятно в центре картины дифракции на круглом отверстии называется «диск Эйри».
Уравнение Эйри
(8.76)
Функция Эйри является частным решением (8.76).
Связь с функцией Бесселя
Сравниваем (8.76) с уравнением Ломмеля
-
,
находим
,
,
,
.
Общее решение
-
,
.
(8.77)
Мнимый аргумент усложняет анализ, ищем другой путь решения.
В
области отрицательного аргумента
уравнение (8.76) получает вид
,
.
(8.78)
Совпадает с уравнением Ломмеля с параметрами
,
,
,
.
Получаем общее решение
,
.
(8.79)
Функция Эйри первого рода
Является
частным решением (8.79) с коэффициентами
.
(8.80)
Условия нормировки
При малом аргументе учитываем (8.11)
-
,
из (8.80) находим
первое слагаемое дает нуль. Нормировка
.
(8.81)
Интегральная нормировка
(8.82)
следует из (8.84). Выполняется
,
.
(8.82а)
Доказательство (8.82а):
При
используем (8.80) и заменяем
,
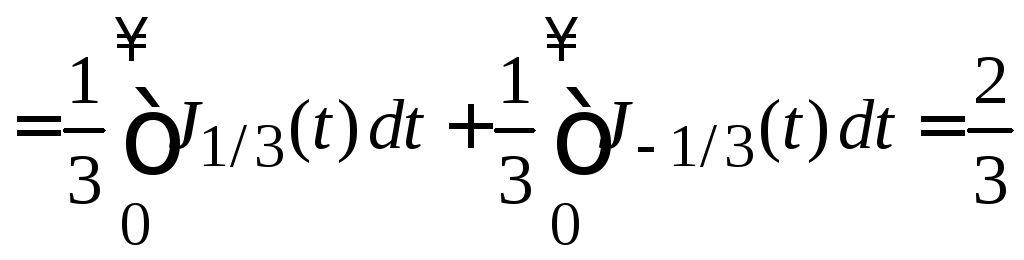где
,
,
.(8.14).
Интегральное представление
Получим
функцию Эйри положительного аргумента
путем решения уравнения Эйри
методом Фурье-преобразования.
Используем
,
(1.35)
.
(1.37)
Преобразование
дает дифференциальное уравнение первого порядка
.
Разделяем переменные
,
интегрируем
.
Выполняем
обратное преобразование Фурье с заменой
.
Подставляем Фурье-образ
.
Находим
с,
вычисляя интеграл при
:
(практическое занятие по теме «Г-функция»).
Сравниваем с условием нормировки
,
(8.81)
находим
.
Функция Эйри выражена через интеграл Эйри
,
(8.83)
Фурье-образ функции Эйри
.
(8.84)
Из
(8.84) при
получаем условие нормировки
.
(8.82)
Предел
При
из (8.80) и (8.12а)
-
,
получаем колебательный характер функции
.
(8.85)
Первые
нули
:
.
Наибольший
максимум
;
.
Предел
Интеграл Эйри
(8.83)
при
вычисляем методом
Лапласа.
Записываем
.
При больших x разлагаем
в
ряд Тейлора около точки экстремума
,
и ограничиваемся первыми тремя членами
ряда
.
Положение экстремума
,
,
где
знак 
выбран из условия, что экстремум
соответствует максимуму, т. е. вторая
производная отрицательна. Получаем
,
,
в результате
.
Из (8.83) находим
,
,
где сделана замена
.
В
полосе (0,
)
отсутствуют полюсы подынтегральной
функции. Поэтому сдвиг линии интегрирования
в комплексной плоскости к вещественной
оси не изменяет интеграла
,
где использовано
.
(П.2.7).
В результате получаем
.
(8.87)
