ФункциЯ Бесселя первого рода

,

Описывает радиальную зависимость в задачах колебаний, волн, теплопроводности, диффузии, теории потенциала.

При функция Бесселя называетсяцилиндрической функцией .В цилиндрических координатах является фурье-образом n-ого порядка по угловой переменной для гармонической волны.

Множество с одинаковым μ образует ортонормированный базис с непрерывным спектром по параметру.

исследовал Даниил Бернулли в 1732 г.

ввел Леонард Эйлер в 1764 г.

Фридрих Вильгельм Бессель составил таблицы J₀, J₁, J₂ для описания движения планет в 1824 г.

Название функциям дал Оскар Шлемильх в 1857 г.

Даниил Бернулли (1700–1782) Леонард Эйлер (1707–1783)

Фридрих Вильгельм Бессель (1784–1846)

Бессель – профессор Кенигсбергского университета, самостоятельно изучил математику и астрономию, в гимназии и в университете не учился. Исследовал комету Галлея, основал обсерваторию в Кёнигсберге, измерил расстояния до звезд по их параллаксам, провел геодезическую съемку территории Восточной Пруссии. Его именем назван кратер на Луне.

Уравнения Бесселя и Ломмеля

Функция Бесселя является частным решением уравнения Бесселя

. (8.1)

Для расширения области применимости уравнения Бесселя усложняем его заменой аргумента и функции, и вводим новые параметры . Это дает уравнение Ломмеля

. (8.2)

Подстановка в (8.2)

,

(8.3)

преобразует (8.2) в (8.1) с аргументом z. При ,уравнение (8.2) переходит в (8.1).

В уравнениях (8.1) и (8.2) величина μ имеет вторую степень, поэтому общее решение (8.2) содержит независимые слагаемые, отличающиеся знаком μ:

. (8.4)

Уравнение получил Евгений Ломмель (1837–1899) в 1868 г.

Интегральное представление Пуассона

Решение уравнения (8.1) методом факторизации дает интегральное представление Пуассона

, (8.5)

где использована формула Эйлера

,

и учтена четность функций косинуса и синуса.

Заменяем

, ,

находим

. (8.6)

Из (8.6) при получаем

, (8.7)

.

Выполняется нормировка

,

,

. (8.8)

Симеон Дени Пуассон (1781–1840)

Пуассон – математик, механик, физик, профессор Парижского университета, окончил Политехническую школу в Париже. Ввел понятие потенциала в электростатику и получил «дифференциальное уравнение Пуассона», связывающее потенциал системы зарядов с их распределением в пространстве. Для случайной величины доказал «распределение Пуассона». Установил связь между продольной и поперечной деформациями тела – «коэффициент Пуассона». Вычислил «интеграл Пуассона», доказал «формулу суммирования Пуассона». В механике ввел «скобки Пуассона» – перестановочные соотношения для величин. Наполеон возвел его в бароны, Луи-Филипп сделал пэром Франции. Цитата – «Жизнь украшается двумя вещами: занятием математикой и ее преподаванием».

Представление в виде степенного ряда

Используем

, (8.5)

подставляем разложение косинуса в ряд Маклорена

,

переставляем суммирование и интегрирование

,

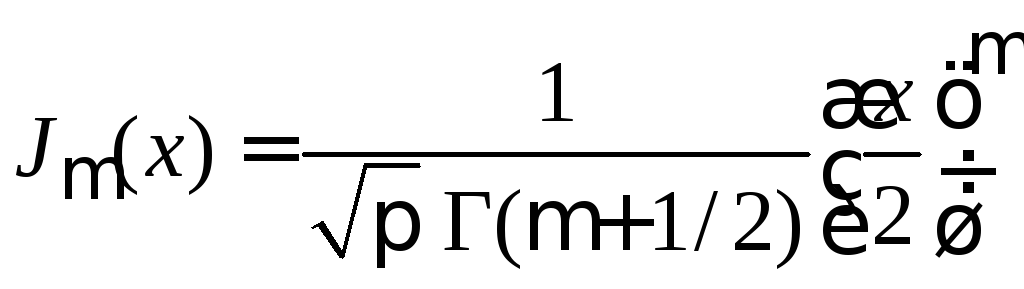
где

.

Замена

,

дает бета-функцию

и получаем разложение функции Бесселя в степенной ряд

. (8.9)

В частности

(8.10)

Предел x  0

Главный вклад в (8.9) при вносит

,

, (8.11)

,

, .

Предел x  

Используем уравнение Ломмеля (8.2) и его решение (8.3)

,

с параметрами ,:

,

.

Выражаем функцию Бесселя

.

При получаем уравнение

,

Находим общее решение

.

В результате

. (8.12)

При функция периодически проходит через нуль, амплитуда колебаний уменьшается.

Детальный анализ дает значения a и A

,

. (8.12а)

Нули функции Бесселя

,

где m – порядковый номер нуля. Для J₀ и J₁ числовой расчет дает

x_0,1 = 2,405; x_0,2 = 5,520; x_0,3 = 8,654; …

x_1,1 = 3,832; x_1,2 = 7,016; x_1,3 = 10,174 …

Нормировка

Выполняется

, (8.14)

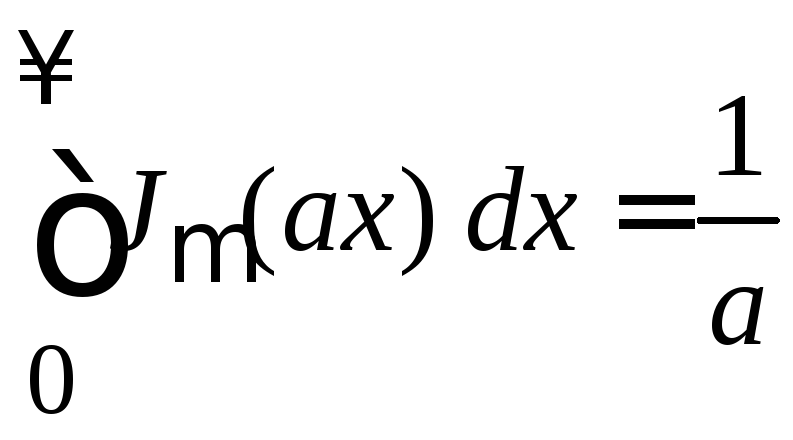. (8.14а)

Доказательство:

Рекуррентное соотношение, которое будет получено далее:

(8.36)

интегрируем по интервалу

, ,

где использовано

, (8.11)

. (8.12а)

Следовательно,

,

не зависит от . Полагаем , учитываем соотношение, которое будет получено в дальнейшем:

, (8.44)

и получаем

.

Площадь под кривой функции Бесселя произвольного порядка равна единице.