ММФ_1 / Matem_-3

КОНЕЧНОЗНАЧНЫЕ СИНГУЛЯРНЫЕ ФУНКЦИИ

Функция Хевисайда

Является функцией включения

(3.1)

Из рис. получаем

. (3.2)

Из определения дельта-функции

,

тогда

,

. (3.3)

Учтено:

если , то ;

если , то .

Из рис. получаем

,

. (3.4)

С учетом (3.4)

.

Меняем знак аргумента функции и используем (3.4)

.

Из последних соотношений

,

. (3.5)

Функция знака аргумента

(3.11)

Свойства

,

,

. (3.12)

Связь с функцией Хевисайда и дельта-функцией

Графически получаем

,

,

, (3.13)

тогда с учетом

(3.3)

находим

. (3.14)

Фурье-образ

,

где

, .

Используем

,

,

получаем

. (3.19)

С учетом

, (3.13)

(2.35)

и (3.19) получаем фурье-образ функции Хевисайда

. (3.20)

По теореме Фурье о парах функций:

если ,

то .

Полагаем

, ,

тогда

,

с учетом

,

,

находим

. (3.21)

Прямоугольная функция

(3.27)

Координаты центра кривой и точек скачка находим из условий на аргумент функции

, ,

получаем

, , .

Свойства

,

,

. (3.28)

Связи с другими функциями

Из графиков функций получаем

,

,

,

, (3.29)

,

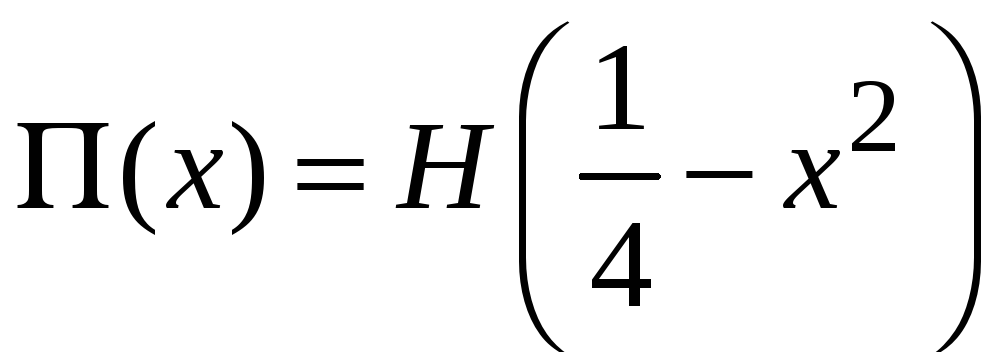где учтены точки скачков

, .

Фурье-образ

,

, (3.31)

, (3.32)

. (3.33)

функция sinc

(3.35)

описывает амплитуду дифрагированной волны на щели шириной A.

,

,

. (3.36)

Экстремумы

|x|	0	1,43	2,46	3,47
	1	–0,22	0,13	–0,09

Фурье-образ

. (3.41а)

Функция имеет спектр постоянный в полосе и нулевой вне этой полосы.

Доказательство (3.41а):

Используем теорему Фурье о парах функций:

если , то .

Полагаем

,

из

, (3.31)

,

с учетом

получаем (3.41а).

Доказать самостоятельно

. (3.41б)

Функция имеет спектр постоянный в полосе , и нулевой вне ее.

Из (3.41б) и при получаем

,

. (3.38)

Площадь под кривой равна единице. Из

, (3.32)

находим

. (3.37)

Усреднение функции по интервалу Т около точки x

. (3.42)

Из

(3.27)

получаем

и находим

. (3.42а)

Усреднение функции по интервалу шириной Т является сверткой этой функции с прямоугольной функцией шириной Т.

Фурье-образ усредненной функции

. (3.42б)

При усреднении функции по интервалу Т ее Фурье-образ модулируется функцией .

Доказательство:

Используем

. (3.42а)

По теореме Фурье о свертке

, (1.24)

с учетом

(3.32)

получаем (3.42).

Треугольная функция

(3.43)

Связь с прямоугольной функцией

Свертка прямоугольных функций является треугольной функцией

. (3.43а)

Доказательство:

,

где учтено

Последний интеграл вычисляется с помощью рисунка.

Усреднение прямоугольной функции по единичному интервалу дает треугольную функцию

Доказательство:

Из определения усреднения

, (3.42а)

при , находим

.

Фурье-образ

Из

, (3.43а)

, (3.31)

и из теоремы Фурье (1.24) о свертке находим

. (3.43а)

Экстремумы sinc²x

|x|	0	1,43	2,46	3,47
sinc2x	1	0,05	0,02	0,01

По теореме Фурье о масштабном преобразовании аргумента

, (1.6)

для треугольной функции шириной 2А получаем

. (3.44)

По теореме (1.21) о парах функций Фурье

,

где

, ,

находим

,

. (3.45)

Функция имеет спектр в виде треугольной функции.

Ортонормированные базисы

НА ОСНОВЕ ПРЯМОУГОЛЬНОЙ ФУНКЦИИ И ФУНКЦИИ SINC

По теореме Фурье об ортонормированном базисе , где : если базис ортонормирован

, (1.16)

то ортонормирован и Фурье-образ базиса

. (1.17)

Ортонормированные базисы:

1. ,

.

2. ,

.

3. ,

.

4. ,

.