
- •Сферическая функция
- •Формулы переходят друг в друга при циклической перестановке
- •Повышающий и понижающий операторы
- •Уравнение СферическОй функциИ
- •Разделение переменных
- •Значение в уравнении
- •Пространственное квантование орбитального момента
- •Сферическая функция
- •Инверсия координат
- •Частные выражения
- •Действие повышающего и понижающего операторов
- •Рекуррентные соотношения
- •Разложение по сферическим функциям
Сферическая функция
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Описывает
угловую зависимость состояния объекта
в сферической системе координат
![]() .
.
Используется для описания вращательного движения, в теории излучения и рассеяния волн и частиц, в теории потенциала.
Определяется как собственная функция оператора момента импульса и оператора Лапласа.
Число
l
связано с модулем момента импульса, m
– с его проекцией на ось z.
Проекция вектора не может быть больше
его модуля, поэтому
![]() ,
для проекции возможны положительные и
отрицательные значения.
,
для проекции возможны положительные и
отрицательные значения.
Набор
![]() образует полный ортонормированный
базис на единичной сфере.
образует полный ортонормированный
базис на единичной сфере.
момент импульса ЧАСТИЦЫ
В классической механике
![]() ,
,
![]() – радиус-вектор
частицы,
– радиус-вектор
частицы,
![]() – импульс. Направление L
определяется правилом
правого винта.
– импульс. Направление L
определяется правилом
правого винта.

В декартовых координатах
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Формулы переходят друг в друга при циклической перестановке
![]() .
.
В квантовой механике величины заменяются операторами
![]() ,
,
![]() ,
,
![]() .
.
Оператор градиента
 ,
(7.1)
,
(7.1)
nk – единичные орты, направленные в сторону перемещения точки при бесконечно малом увеличении соответствующего аргумента.
Операторы момента импульса
![]() ,
,
 ,
,
 ,
,
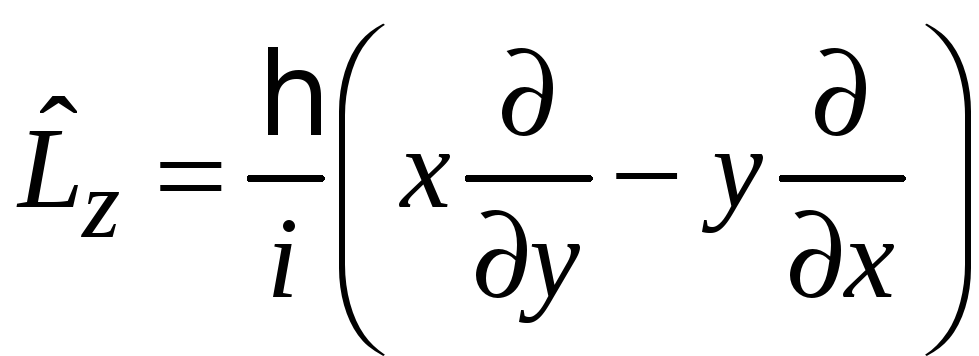 ,
,
![]() .
(7.2)
.
(7.2)
Формулы переходят друг в друга при циклической перестановке
![]() .
.
Сферические координаты

![]() ,
,
![]() ,
,
![]() .
(7.3)
.
(7.3)

Оператор градиента
 ,
(П.8.1)
,
(П.8.1)
![]() – единичные
орты. Операторы
момента импульса
– единичные
орты. Операторы
момента импульса
 ,
(7.4)
,
(7.4)
 .
(7.5)
.
(7.5)
Оператор Лапласа
Выражается через квадрат момента импульса
 ,
(7.6)
,
(7.6)
определяет кинетическую энергию частицы.
Радиальная часть оператора Лапласа
 .
(7.7)
.
(7.7)
Перестановочное соотношение операторов (коммутатор)
![]() .
.
Предполагается, что правее каждого слагаемого находится функция, на которую действуют операторы:
![]() .
.
Выполняются
![]() ,
,
![]() .
.
Если
операторы коммутируют, т. е. их можно
переставлять
![]() ,
то соответствующие им физические
величины измеримы одновременно с
неограниченной точностью. Если коммутатор
операторов не равен нулю, то чем точнее
измеряется одна величина, тем больше
неустранимая погрешность другой
величины.
,
то соответствующие им физические
величины измеримы одновременно с
неограниченной точностью. Если коммутатор
операторов не равен нулю, то чем точнее
измеряется одна величина, тем больше
неустранимая погрешность другой
величины.
Для операторов момента импульса
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
(7.8)
.
(7.8)
Определенные
значения имеют одновременно квадрат
модуля момента импульса
![]() и одна из его проекций
и одна из его проекций
![]() .
.
Повышающий и понижающий операторы
![]() ,
,
![]() .
(7.9)
.
(7.9)
Действуя
на сферическую функцию
![]() ,
операторы
,
операторы
![]() изменяют на единицу
число m,
т. е. проекцию вектора момента импульса
на ось z.
изменяют на единицу
число m,
т. е. проекцию вектора момента импульса
на ось z.
Выполняются
![]() ,
,
![]() ,
(7.11)
,
(7.11)
![]() .
(7.12)
.
(7.12)
Доказательство (7.12):
![]()
![]() ,
,
где использовано
![]() .
(7.8)
.
(7.8)
