Теорема о свертке

Фурье-образ свертки функций равен произведению их фурье-образов

. (1.24)

Доказательство:

.

Расцепляем интегралы заменой аргумента ,и учтитываем

.

Выполняется

. (1.25)

Доказательство:

.

Под интегралом сделана замена .

Теорема о произведении

Фурье-образ произведения функций равен свертке их фурье-образов

,

. (1.26)

Доказательство:

Выполняем фурье-преобразование (1.25)

и используем интегральную теорему (1.20)

.

Теорема о дифференцировании

При дифференцировании функции ее Фурье-образ умножается на

. (1.35)

Доказательство:

Формулу

, (1.2)

дифференцируем n раз

.

Сравниваем результат с (1.2), получили для функции Фурье-образ.

Умножение функции на

Умножение функции на приводит к дифференцированию ее Фурье-образа

,

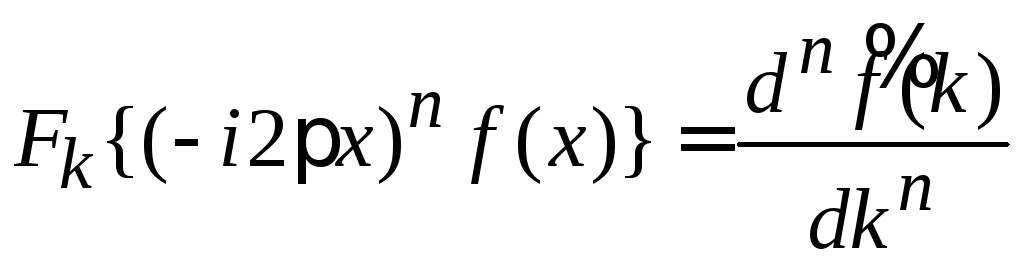. (1.37)

Доказательство:

Используем

, (1.1)

получаем

.

Сравнение результата с (1.1) дает (1.37).

Преобразование периодических функций

Для функции с периодом L

спектр является дискретным, и получается разложением функции по базису гармонических функций с периодами , где

Базисы из комплексных периодических функций

,

Периодическими комплексными функциями с периодом являются

.

Доказательство:

,

где учтено

,

Получаем базис

• , – период.

Переход к другому периоду осуществляется заменой аргумента:

• : ,– периодL.

• : ,– период.

Базисы из вещественных периодических функций

,

, ,

Ортонормированность базисов

Для базиса выполняется условие ортонормированности

.

, :

.

, :

, (1.43)

где сделаны замены

, .

Выполняется:

,

,

. (1.45)

,

,

. (1.46)

Преобразование Фурье комплексной функции с периодом L

По ортонормированному базису периодических гармонических функций

разлагаем и получаемряд Фурье

. (1.48)

Ищем коэффициенты , выполняя

.

Переставляем суммирование и интегрирование, и учитываем

. (1.43)

Все слагаемые суммы дают нули кроме слагаемого . Переобозначая, получаем

. (1.49)

Спектр периодической функции

Подстановка (1.48) в преобразование Фурье

(1.1)

после перестановки суммирования и интегрирования

с учетом

(2.24)

дает

. (1.47)

Периодическая функция имеет дискретный спектр в виде модулированной гребенчатой функции.

Дифференцирование

Выполняем 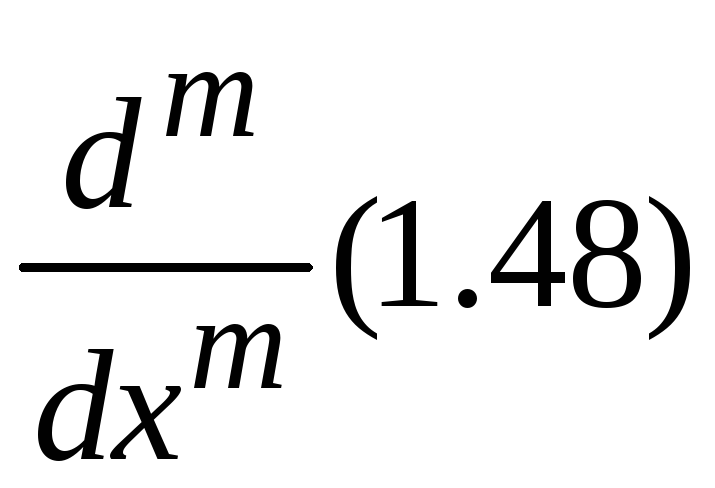и получаем, что, если

,

то

. (1.50)

Ряд Фурье для вещественной периодической функции

Исследуемая функция удовлетворяет

,

.

Из

(1.49)

получаем

,

тогда

.

Из

(1.48)

получаем

, (1.53)

где использовано

.

Замена

,

,

где b_n и c_n – вещественные, дает разложение функции в ряд Фурье

, (1.54)

где

,

,

,

где учтено

.