Теорема о частотной полосе

, (1.8)

где дисперсии

; .

Уменьшение пространственной протяженности функции приводит к увеличению ее частотной протяженности , и наоборот.

Равенство в (1.8) выполняется для функции Гаусса

,

,

, ,.

Смещение аргумента

. (1.9)

Доказательство:

Используем (1.1)

,

получаем

.

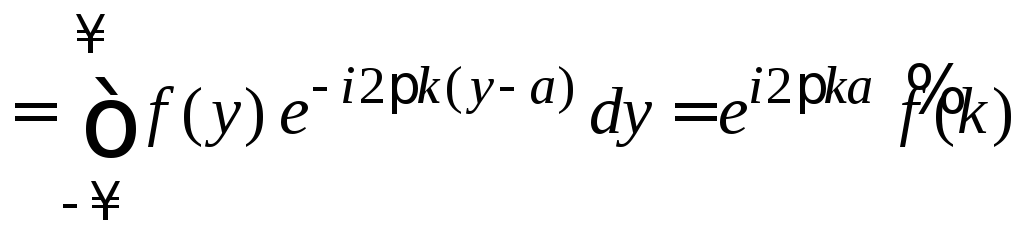Фазовый сдвиг

. (1.10)

Доказательство:

Из (1.1)

.

Комплексное сопряжение

, (1.11)

Доказательство:

Из (1.1)

,

.

Следствия (1.7) и (1.11)

,

:

1) если – четная и вещественная, то вещественная.

Доказательство:

Используем

,

,

тогда

;

2) если – вещественная и нечетная, то мнимая;

3) если – мнимая и четная, то мнимая;

4) если – мнимая и нечетная, то вещественная.

Теорема Парсеваля

. (1.14)

В физике выражает закон сохранения энергии и вероятности при преобразовании Фурье.

Доказательство:

Используем (1.1) и (1.2)

,

.

Получаем

,

тогда

=,

где изменен порядок интегрирований.

Обобщенная теорема Парсеваля

. (1.15)

При иполучаем (1.14).

Ортонормированность базиса и его образа

Если функции ортонормированны

, (1.16)

то их фурье-образы также ортонормированны

. (1.17)

В (1.14) полагаем и.

Интегральная теорема

Прямое и обратное преобразования восстанавливают непрерывную функцию

,

. (1.20)

Доказательство: Из

, (1.1)

, (1.2)

с заменой порядка интегрирований

,

где использованы свойства дельта-функции:

,

.

Следовательно, для непрерывной функции получаем операторы тождественного преобразования:

, . (1.20а)

Теорема о парах функций и

Если

,

то

. (1.21)

Доказательство:

Используем (1.1), заменяем аргумент , полученный интеграл сравниваем с (1.2)

.

Преобразование Фурье

, (1.1)

. (1.2)

Свертка функций

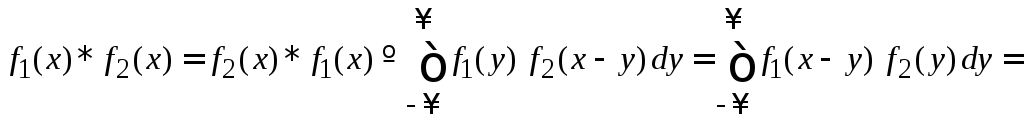
, (1.22)

где выполнена замена аргумента

с параметрами

, ;,;,

и использовано

.

Физический смысл свертки для линейного и стационарного преобразователя сигналов

f₁(t') – входящий сигнал (например, ЭДС) в момент t',

f₂(t) – выходящий сигнал (например, ток) в момент t.

Выполняются:

1) принцип суперпозиции – входящие сигналы для разных моментов времени преобразуются независимо, не влияя друг на друга, поэтому преобразование линейное;

2) принцип причинности – если входящий сигнал включается в момент t', то выходящий сигнал отсутствует при более ранних временах t < t';

3) принцип однородности – реакция преобразователя в момент t на сигнал, поступивший в момент t', не изменяется при сдвиге начала отсчета времени, поэтому реакция зависит от (t – t'). Однородность по времени выполняется для стационарного преобразователя с постоянными параметрами.

Принципам удовлетворяет свертка

,

где

–функция Грина – реакция преобразователя на импульсный входящий сигнал;

–функция включения;

–аппаратная функция.

Выходящий сигнал линейного стационарного преобразователя является сверткой входящего сигнала и функции Грина преобразователя.