Полиномы Лежандра

, ; ; ;

– описывают угловую зависимость в полярных и сферических координатах;

– входят в собственные функции оператора момента импульса и оператора Лапласа;

– множество образует ортонормированный базис на интервале.

Полиномы исследовал Андре Мари Лежандр в 1785 г.

Уравнение Лежандра

, (6.93)

Учитываем

,

тогда

. (6.93а)

Для угловой переменной

, ,

,

из (6.93а) для получаем

. (6.94)

Метод факторизации

1. Уравнение

(6.93)

гипергеометрического типа

.

2. Сравнение дает

,

, ,,,

, ,

,

,

, ,

,

.

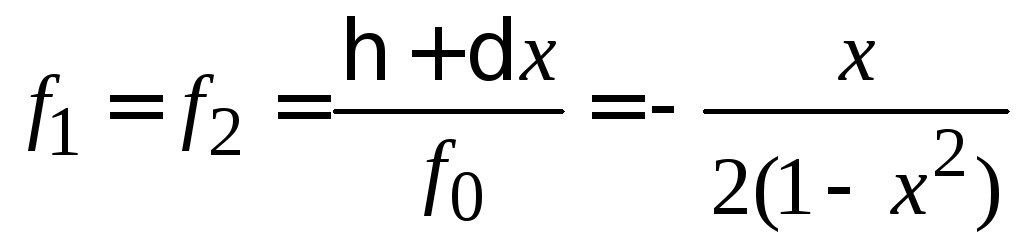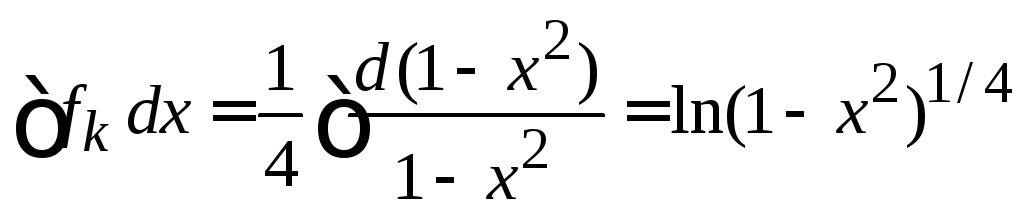3. Граничные условия

в виде

дают

, .

4. Весовая функция

,

.

5. Решение Родрига

дает

.

Полагаем

,

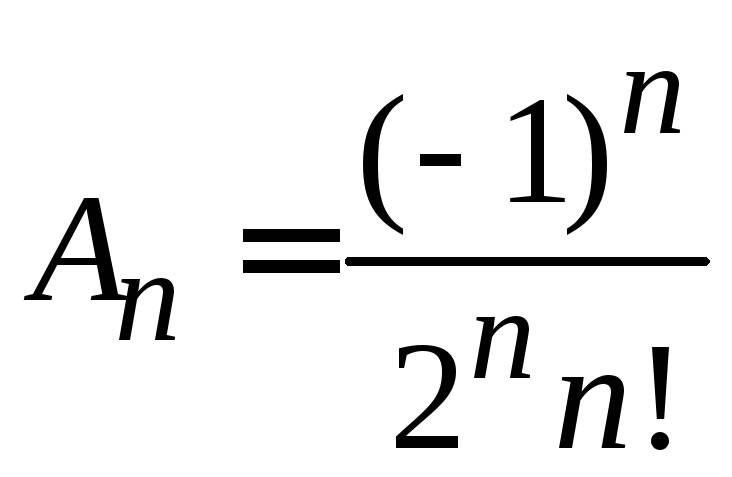получаем форму Родрига для полинома Лежандра

. (6.96)

Свойство четности

, (6.97)

тогда

, n – нечетное.

6. Ортонормированность

, .

Учитываем

, ,,

, ,,

,

,

,

где использовано (П.2.3)

при ,,. Получаем условие ортонормированности

. (6.112)

7. Производящая функция

,

с учетом

получает вид

.

Уравнение для ξ

, ,

где имеет вид

.

Находим решение

,

где выбор знака + обеспечивает требуемое поведение при

.

Использовано

, .

Из

,

с учетом

,

получаем

.

Заменяем , тогда

, (6.101)

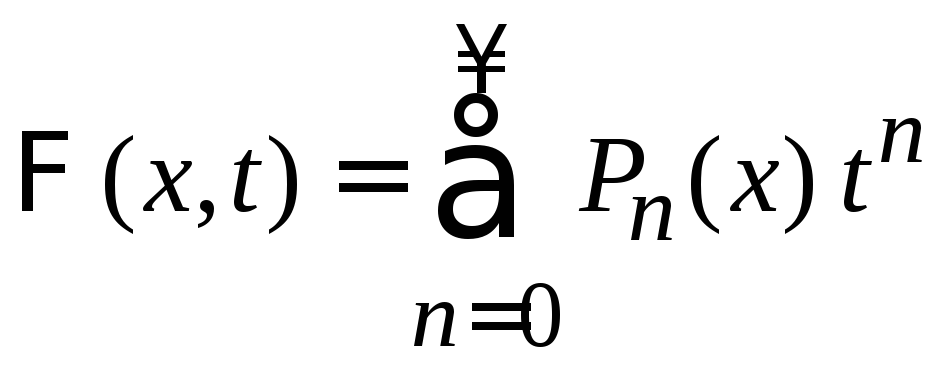. (6.102)

Форма полинома

Форму Родрига (6.96)

выражаем через полином. Используем бином Ньютона

1. При ,получаем

,

.

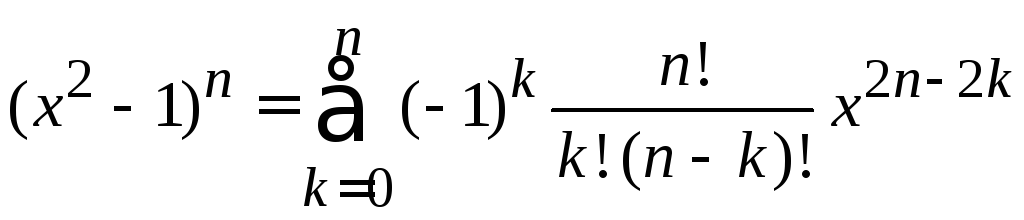Подстановка в (6.96) дает первую полиномиальную форму

. (6.98)

Следовательно, n – порядок полинома.

3. Преобразуем

.

Используем бином Ньютона

.

При ,находим

тогда

,

.

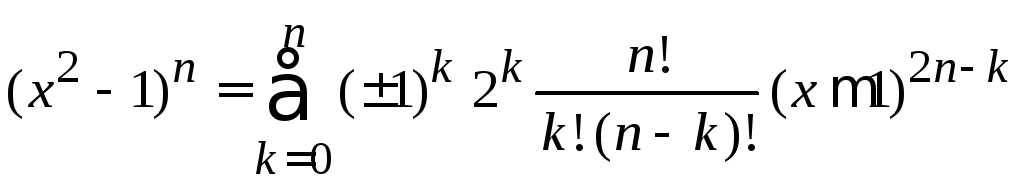Из (6.96)

находим

.

Заменяем , и получаемвторую полиномиальную форму

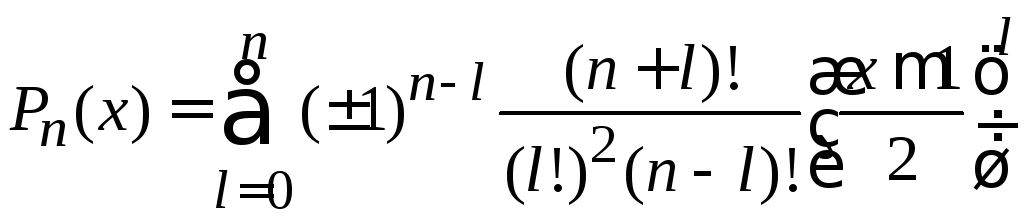. (6.99)

Из (6.99) находим значения полинома на границах области определения при

, . (6.100)

Полиномы низших порядков

Из (6.96) и (6.98)

,

находим

,

,

,

,

.

Рекуррентные соотношения

Используем выражение и определение производящей функции

, (6.101)

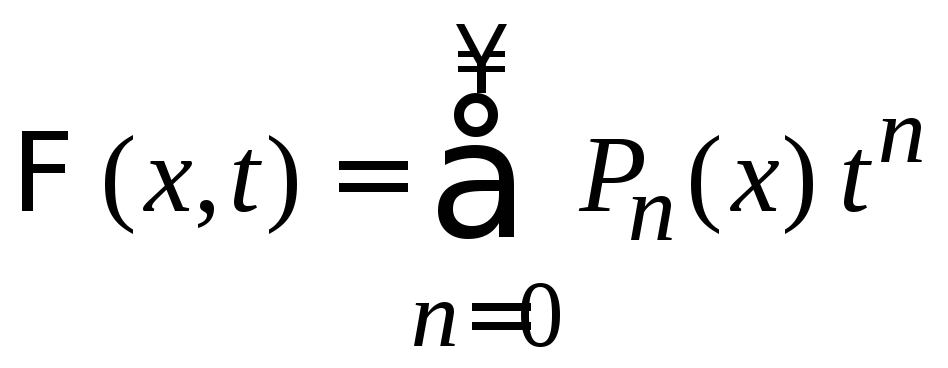. (6.102)

1. Дифференцируем (6.101) по x и получаем

.

Подставляем (6.102)

,

приравниваем коэффициенты при

,

получаем

. (6.103)

2. Дифференцируем (6.101) по t

.

Подставляем (6.102)

.

Сравниваем коэффициенты при t ⁿ

,

получаем

. (6.104)

3. Дифференцируем (6.104)

. (6.104а)

4. Исключаем из (6.104а) и (6.103)

. (6.105)

5. Исключаем из(6.104а) и (6.103)

. (6.106)

6. В (6.106) заменяем

.

Исключаем с помощью (6.105)

, (6.107)

7. Складываем (6.106) и (6.105)

. (6.110)

Разложение функции по полиномам Лежандра

Функцию , определенную при, разлагаем в ряд

. (6.113)

Для нахождения коэффициентов умножает (6.113) на, результат интегрируем по интервалуи учитываем (6.112)

.

Получаем

.

После замены находим коэффициент

.

Подстановка формы Родрига (6.96)

,

дает

.

Интегрируем по частям n раз и получаем

. (6.114)

Соотношение Лежандра

Для векторов r и r₀, выходящих из одной точки под углом  друг к другу выполняется

, . (П.6.4)

Соотношение используется в теории электромагнитного поля.

Доказательство:

Учитываем

,

.

Замена , дает

.

Сравниваем с производящей функцией полиномов Лежандра (6.101) и (6.102)

,

.

Находим

.

Замена и дает

, . (П.6.4)

При для сходимости ряда заменяем в (П.6.4)

, . (П.6.4а).

Разложение потенциала диполя по мультиполям

Потенциал поля диполя в точке A в СГС

.

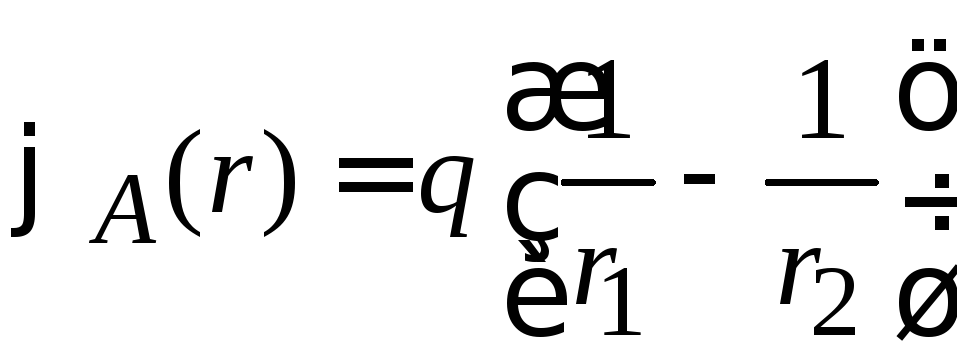Положения зарядов относительно точки симметрии O определяем векторами и, положение точки наблюдения – вектором.

При выполняется разложение

, (П.6.6)

где –мультиполя; ; θ – угол между направлением дипольного момента и направлением на точку наблюдения.

Доказательство:

Используем

, ,

тогда

, .

Используем (П.6.4)

,

.

Учтено, что при замене , получаем

, ,.

Вычитаем друг из друга последние выражения и находим

.

Четные слагаемые сокращаются, нечетные слагаемые удваиваются, и дают (П.6.6)

.

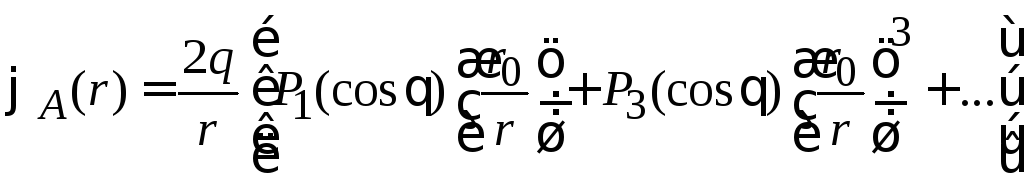На большом расстоянии от диполя при главный вклад вносит первое слагаемое, тогда

, (П.6.7)

где ;–дипольный момент.