Решения для низших значений квантовых чисел

–основное состояние ;

,

.

Нормировка вероятности

Вероятность обнаружения электрона в шаровом слое радиусом r единичной толщины равна

.

Вероятность найти электрон во всем пространстве равна единице, и в сферических координатах находим условие нормировки радиальной функции

, ,

.

Для безразмерной получаем

. (6.88)

Докажем, что функция (6.87) удовлетворяет (6.88).

Подстановка (6.87)

в (6.88) с учетом дает

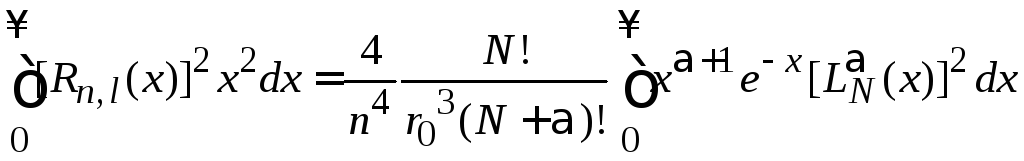. (6.88а)

Для вычисления интеграла используем (6.76)

при

, .

Находим

.

Подстановка интеграла в (6.88а) дает (6.88).

Рекуррентные соотношения

1. Равенство (6.58) для полиномов Лагерра с одинаковыми порядками α

умножаем на 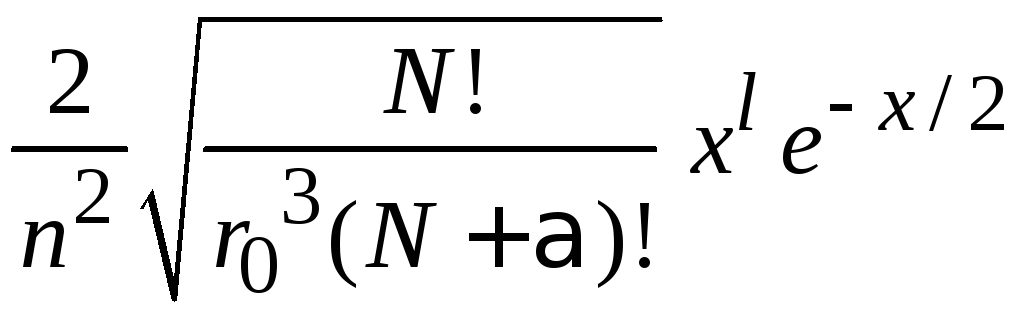и с учетом (6.87)

,

, ,

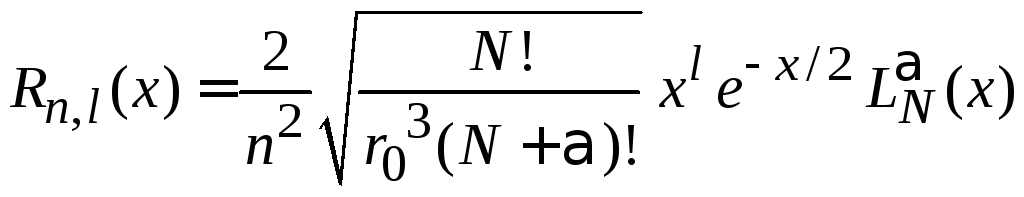получаем соотношение между функциями с одинаковыми l

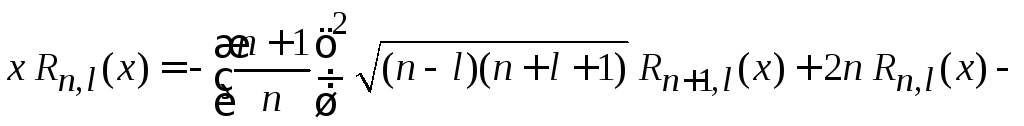
– . (6.89)

2. Дважды используем (6.59)

,

находим

,

.

В результате

.

Заменяем

, ,

получаем

.

Умножаем равенство на

,

и сравниваем с (6.87)

,

приходим к соотношению, где индекс l у функции, стоящей слева, на единицу меньше, чем у функций, стоящих справа:

–. (6.90)

3. Используя (6.57) и (6.61), находим

.

Выражая с помощью (6.58) и заменяя, получаем

.

Полагая ,и умножая на , находим соотношение, где индекс l у функции, стоящей слева, на единицу больше, чем у функций, стоящих справа:

. (6.91)

4. Дифференцируем (6.87)

,

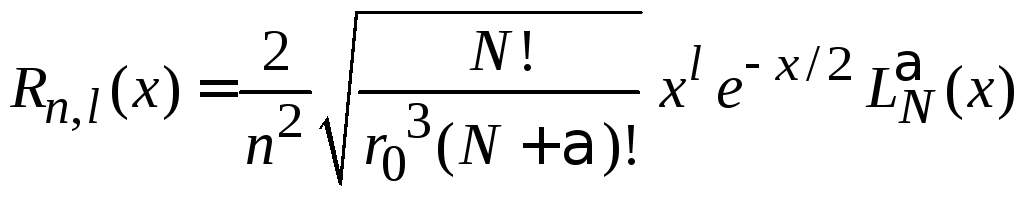используем (6.54)

,

получаем

.

Используем рекуррентные соотношения (6.58) и (6.61), которые выравнивают верхний индекс и убирают множитель x из круглой скобки:

.

В результате

– . (6.92)

Вычисление матричных элементов

По определению

, (1)

.

1. Среднее расстояние до ядра электрона в состоянии.

С учетом оператора радиуса и радиального объема , находим

,

где сделана замена . Вычисляем интеграл с помощью рекуррентного соотношения(6.89), устраняющего x под интегралом, и условия ортонормированности (6.86)

– ,

.

При возведении в квадрат рекуррентного соотношения условие ортогональности зануляет перекрестные произведения, остается сумма квадратов слагаемых

.

С учетом нормировки

,

,

,

находим

.

В результате

. (П.5.8)

2. Рекуррентное соотношение Крамерса

, (П.5.10)

где

; .

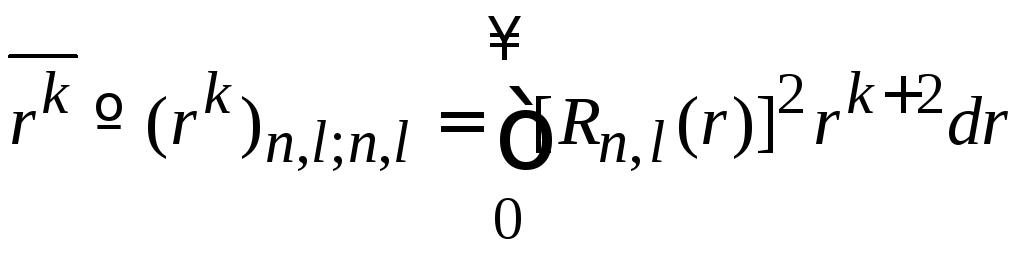Доказательство:

• Интегрируем

по частям, где

, .

Свободное слагаемое обращается в нуль, получаем

.

В результате

.

• Аналогично находим

,

,

где

.

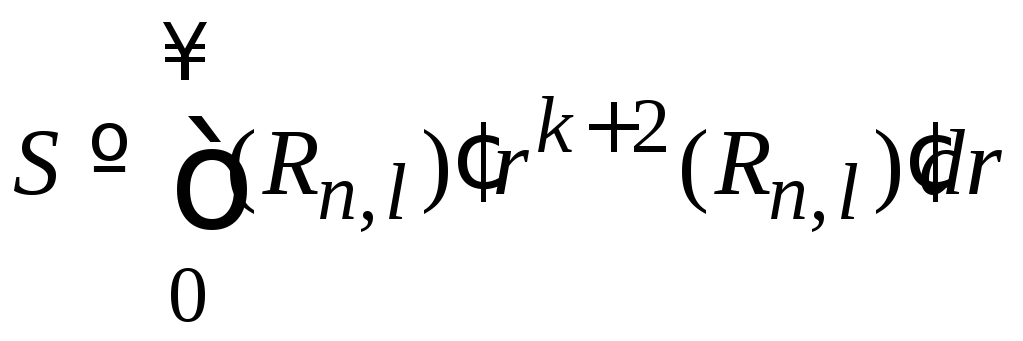• Используем уравнение Шредингера для радиальной функции

. (П.5.11)

Умножая уравнение на , интегрируем и получаем

.

Умножаем (П.5.11) на , интегрируем и находим

.

• Исключая S из уравнений, получаем (П.5.10).

Частные случаи

1. При из(П.5.10)

,

находим

,

,

– теорема вириала связывает полную энергию со средним значением потенциальной энергии .

2. При получаем (П.5.8)

.

3. При находим

.

Соотношение (П.5.10) не позволяет найти .