Обобщенные полиномы Лагерра

, ;– любое число;.

Набор полиномов образует ортонормированный базис на полуоси .

Используются:

• в теории измерительной техники и в теории систем связи;

• в квантовой механике описывают радиальное движение электрона в атоме.

Полиномы исследовал Эдмон Никола Лагерр в 1878 г.

Обобщенные полиномы изучал Николай Яковлевич Сонин в 1880 г., поэтому их называют такжеполиномами Сонина–Лагерра.

Уравнение Лагерра

(6.41)

является гипергеометрическим уравнением.

Форма Родрига

Методом факторизации ранее получена весовая функция (П.3.9)

.

В решении уравнения в форме Родрига (П.3.10) выбираем постоянную

,

и находим

. (6.42)

Полиномиальная форма

, (6.44)

следовательно, n – высшая степень полинома .

Доказательство (6.44):

Используем форму Родрига (6.42). Дифференцирование произведения функций проводим по формуле Лейбница

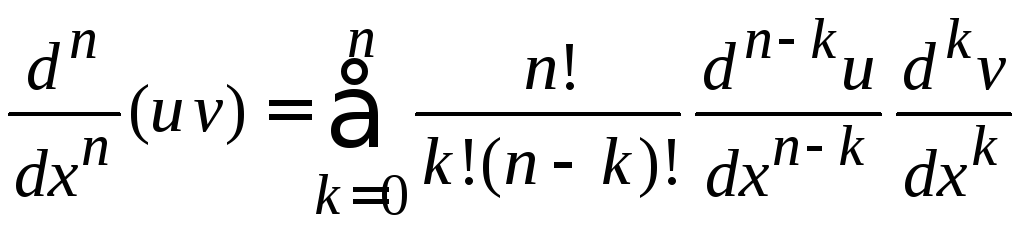. (6.45)

Например, при получается известная формула

.

В (6.45) полагаем ,и учитываем

.

Соотношение

обобщаем на случай – не целое

.

В результате

.

Подставляем в (6.42)

,

получаем полином порядка n

. (6.44)

При находим

. (6.47)

Полиномы низших степеней

Из (6.42) и (6.44) получаем

,

,

,

.

При для обычных полиномов Лагерра –

,

,

,

.

Производящая функция

Методом факторизации ранее получено

. (6.52)

По определению (5.14)

с учетом получаем

. (6.53)

Рекуррентные соотношения

1. Дифференцируем (6.52) по x

.

Подставляем (6.53)

.

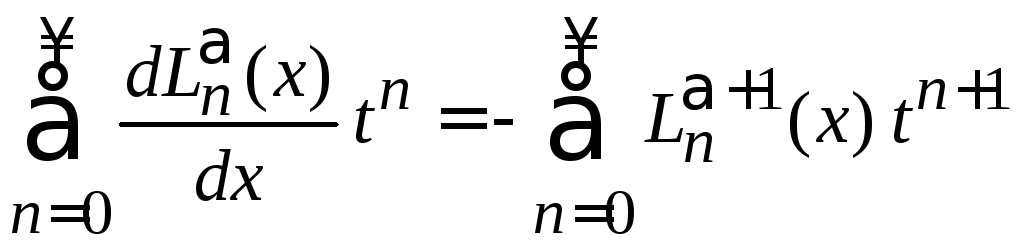Приравниваем коэффициенты при

. (6.54)

2. Последовательно дифференцируем далее (6.54) и получаем

, . (6.55)

В (6.55) при

.

Заменяем и получаем выражение обобщенного полинома Лагерра через полином Лагерра

. (6.56)

3. В уравнение Лагерра (6.41)

подставляем (6.54)

,

,

получаем

. (6.57)

4. Выражение (6.52)

дифференцируем по t и приходим к уравнению

.

Подставляем (6.53)

,

получаем

.

Приравниваем коэффициенты при

.

Приводим подобные

. (6.58)

5. Из (6.52)

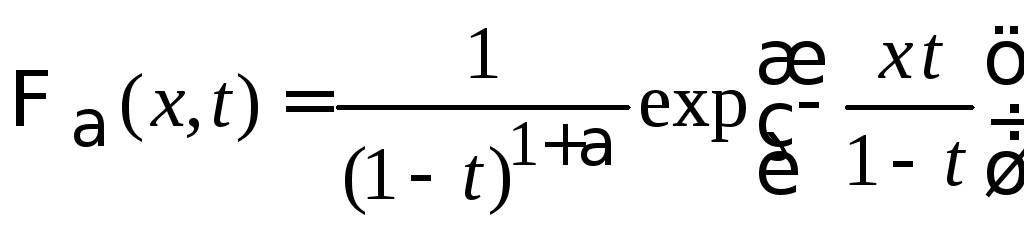
Следует

.

Подставляем (6.53)

,

получаем

.

Приравниваем коэффициенты при

. (6.59)

6. В (6.58) перегруппировываем слагаемые

.

Используем (6.59)

,

,

получаем

. (6.60)

Заменяем и

. (6.61)

7. Из (6.58) в виде

вычитаем (6.61) и получаем

. (6.64)

Ортонормированность

Методом факторизации ранее получено (П.3.11). Доопределяем и получаем

. (6.67)

Разложение функции по ортонормированному базису

Функцию , определенную при , разлагаем по базису

. (6.68)

Ищем коэффициенты разложения. Умножаем (6.68) на , интегрируем, учитываем ортонормированность (6.67). В сумме остается лишь одно слагаемое за счет символа Кронекера. После заменыполучаем

.

Подстановка (6.42)

дает

.

Интегрируем по частям n раз, свободные слагаемые равны нулю на обоих пределах. Получаем коэффициент

. (6.69)

Интегралы с полиномами Лагерра

1. Вычисляем

, r – целое.

Подстановка (6.42)

дает

.

Интегрируем по частям n раз и получаем

,

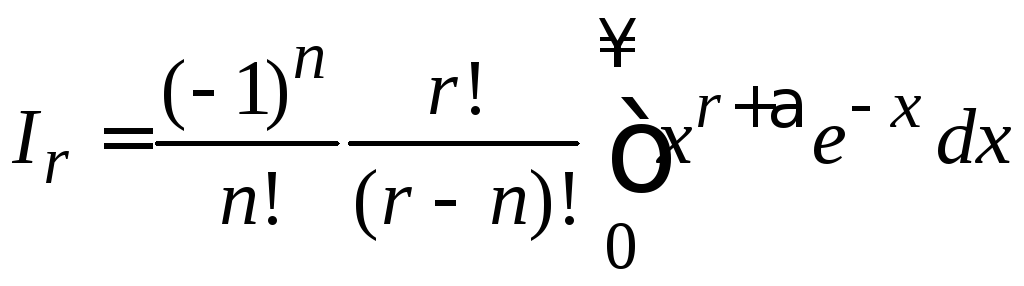где учтено

.

Используем определение гамма-функции (4.1)

,

находим

, , (6.70)

, . (6.71)

Из (6.70) при и

, (6.72)

. (6.73)

2. Вычисляем

, r – целое.

Интеграл сводим к (6.70)

подстановкой полиномиальной формы (6.44)

.

Получаем

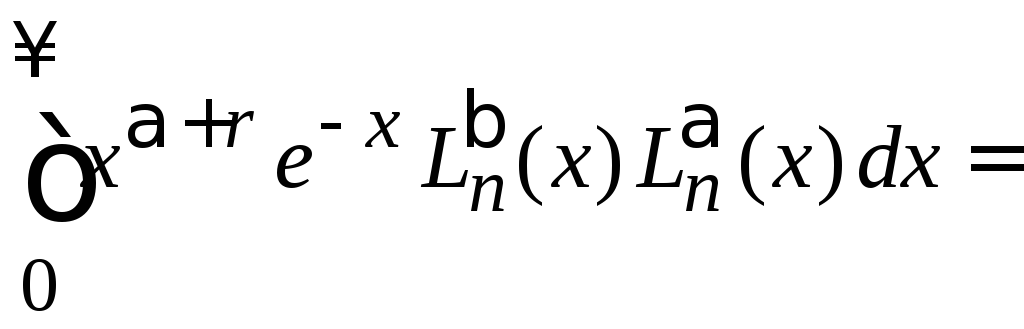
=. (6.74)

Ограничение нижнего предела суммирования по k вызвано множителем .

При в сумме (6.74) остается одно слагаемоеи результат не зависит от величины β

, (6.75)

что доказывает нормировку в условии ортонормированности (6.67).

При получаем

. (6.76)

3. Вычисляем интеграл, отличающийся от (6.70) знаком перед r:

, r – целое, .

В (6.70)

заменяем , где, и учитываем

,

где использовано (4.4)

.

(6.70) после замены получает вид

, . (6.77)

Из (6.77) при инаходим

, , (6.79)

, (6.80)

4. Вычисляем

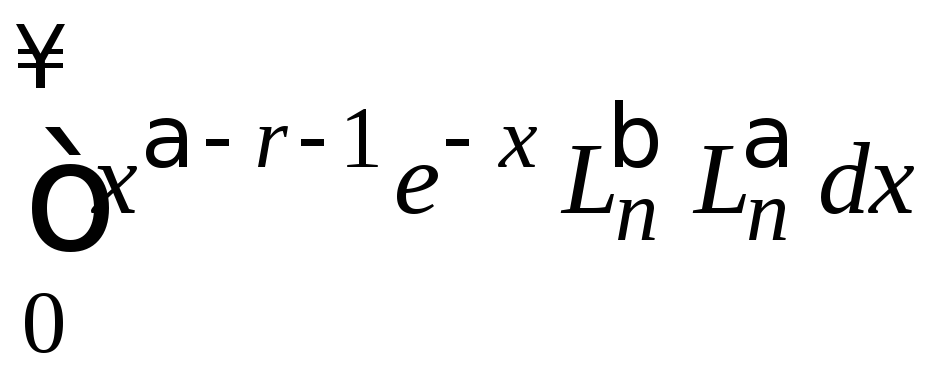, r – целое.

Интеграл сводится к (6.77)

если использовать (6.44):

.

Получаем

. (6.81)

При и

, (6.82)

. (6.83)