Соотношения между матричными элементами
Для эрмитового оператора выполняется
.
(4)
Комплексное сопряжение обращает направление перехода между состояниями, т. е. обращает течение времени:
.
Доказательство:
С учетом (1)
,
получаем
.
Третье равенство получено из эрмитовости оператора.
Матричный элемент произведения эрмитовых операторов выражается через матричные элементы каждого из них
.
(5)
Переход
под действием
произведения операторов
происходит через все возможные
промежуточные состояния
k,
в которых
оказывается система под действием
оператора
.
При
доказательстве (5) используется полнота
базиса функций состояния
и фильтрующее свойство дельта-функции.
Примеры
1. Для матричного элемента оператора координаты гармонического осциллятора доказать
,
(П.4.6)
где
– безразмерная,
.
Для
оператора
по определению
.
Интеграл
сводится к формуле ортонормированности
базиса
,
если устранить множительx
под интегралом. Для этого используем
рекуррентное соотношение (6.34)
,
получаем
.
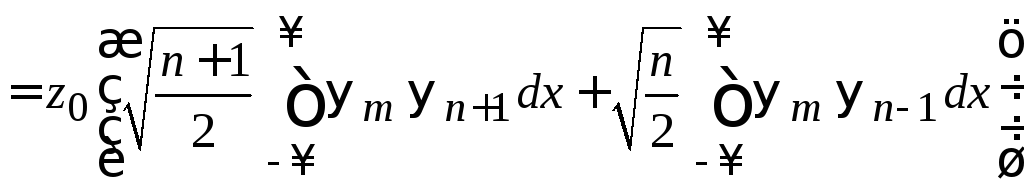Используем условия ортонормированности (6.33)
,
получаем
,
(П.4.6)
В частности
,
,
.
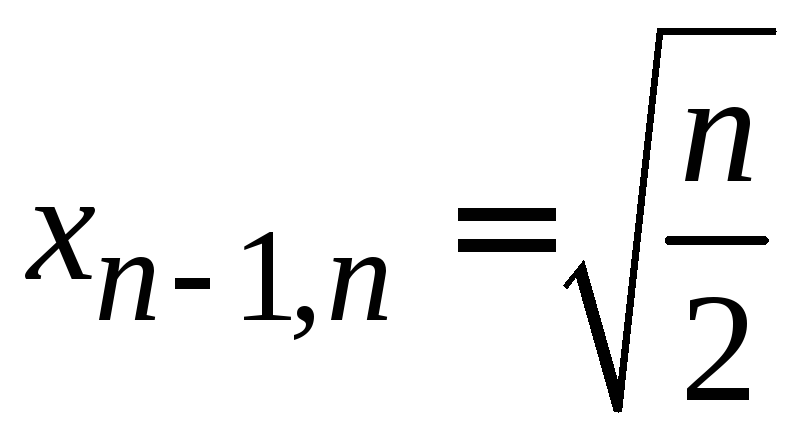(П.4.7)
Среднее значение координаты осциллятора в любом состоянии равно нулю, что очевидно из симметрии колебаний относительно положения равновесия.
Матричные элементы вещественные, тогда из
(4)
получаем
.
2.
Для оператора импульса
найти матричный
элемент
,
где
;
;
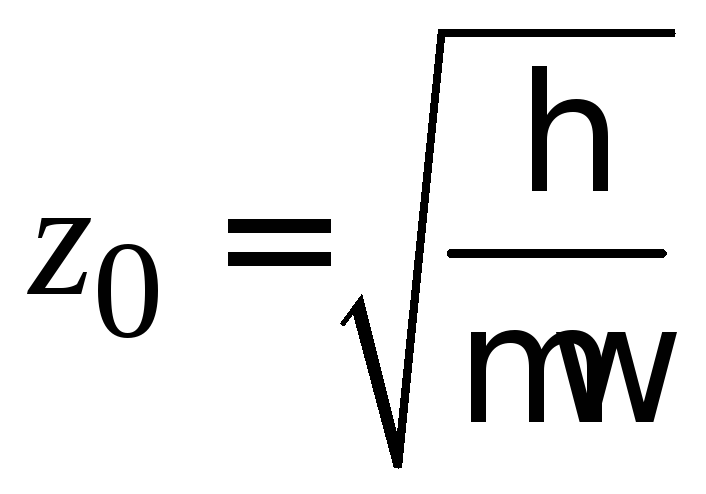– безразмерная.
Интеграл
в 
сводится к формуле ортонормированности
после устранения
производной под интегралом. Для этого
используем рекуррентное соотношение
(6.39)
.
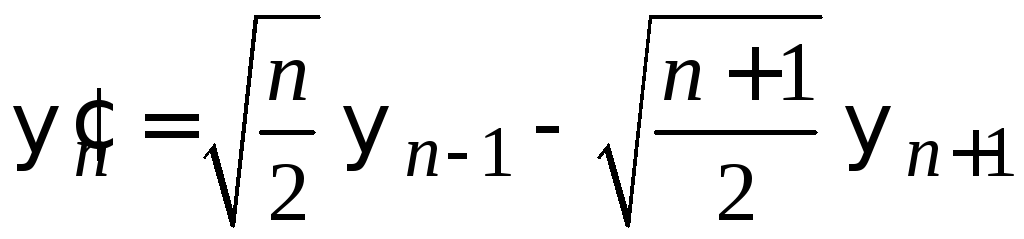Получаем
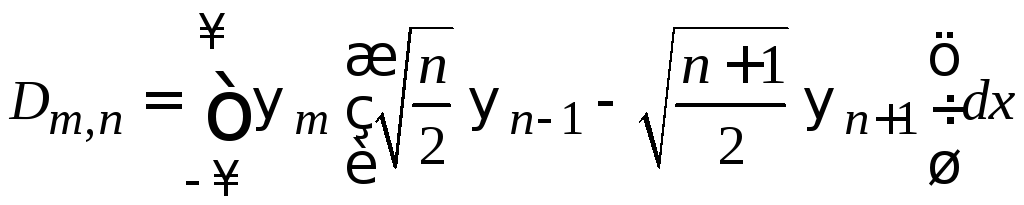
Вычисляем интегралы при помощи условия ортонормированности
,
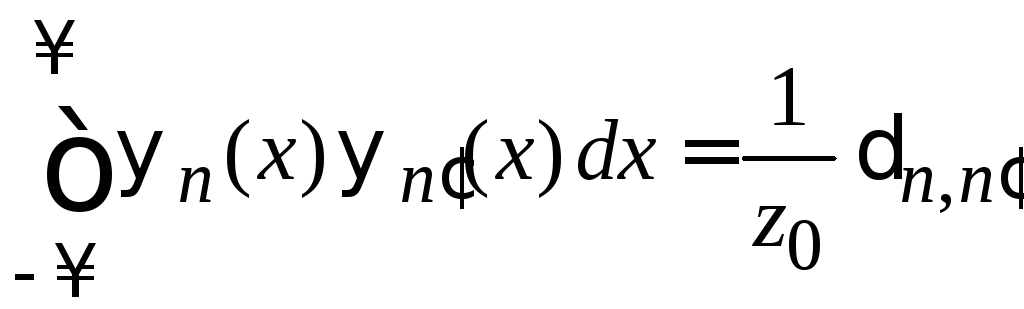находим
.
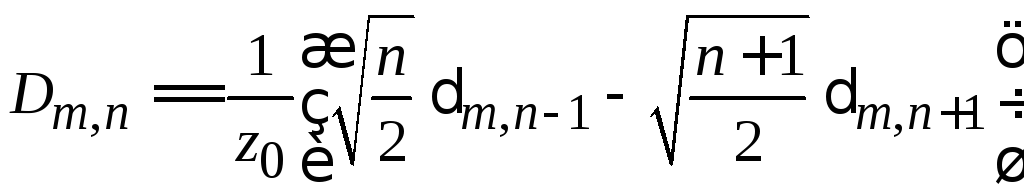Частные результаты:
,
,
.
Матричные элементы импульса:
,
(П.4.11)
,
,
,
,
,
среднее значение
.
(П.4.12)
Среднее значение проекции импульса осциллятора в любом состоянии равно нулю, что очевидно из симметрии колебаний по- и против оси x.
3. Доказать, что фурье-преобразование не изменяет форму уравнения гармонического осциллятора.
Фурье-преобразование уравнения (6.31)
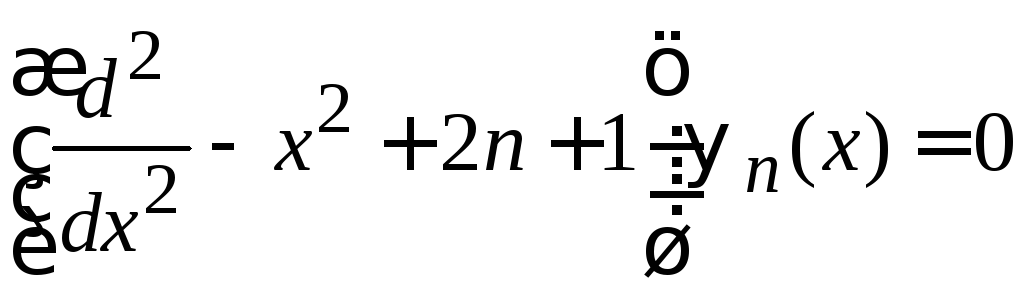
с учетом теорем Фурье
,
(1.35)
(1.37)
дает
.
Заменяем
,
получаем уравнение
,
(П.4.14)
аналогичное
(6.31), где
– безразмерный импульс;
.
(П.4.15)
4. Для полиномов Эрмита доказать формулу Мелера
,
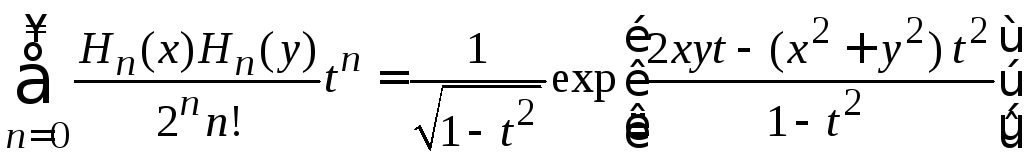(П.4.20)
где
.
Получить формулу при
.
Используем интегральное представление полиномов Эрмита (6.8)
,
.
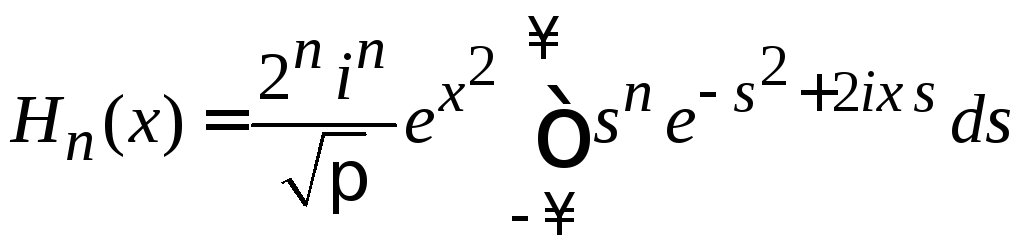Меняем порядок суммирования и интегрирований
.
Используем
,
тогда
.
Используем (П.2.5)
при
,
,
,
и вычисляем внутренний интеграл
,
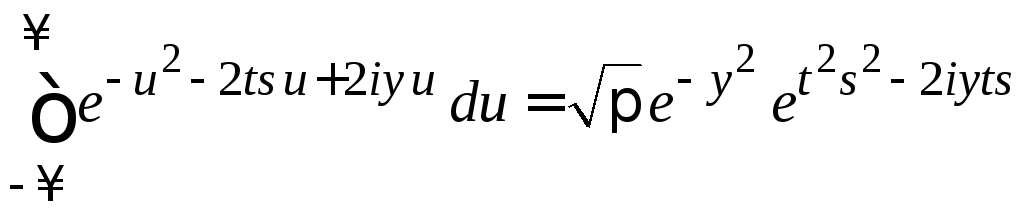тогда
.
(П.4.20а)
Интеграл находим при помощи (П.2.5)
,
,
и получаем (П.4.20).
При
последний интеграл дает дельта-функцию
,
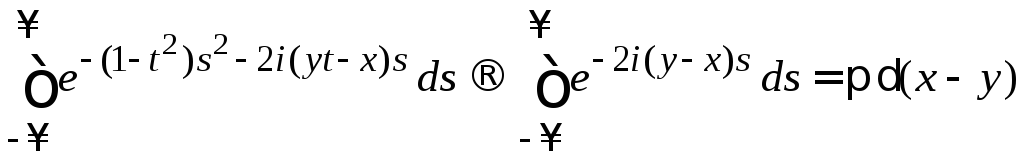где учено (2.24)
.
Из
(П.4.20а)
получаем условие
полноты базиса из полиномов Эрмита
.
(П.4.21)
Для
функций гармонического осциллятора
,
где
,
(6.32)
получаем условие полноты базиса функций гармонического осциллятора
.
(П.4.22)